1 Cover
2 Preface
3 1 Data Analysis and Understanding 1.1 Exploring the Distribution of Data 1.2 Exploring Prediction Using Data Problems
4 2 Classical Probability 2.1 Experiments with Equally Likely Outcomes 2.2 Probability Laws 2.3 Counting Methods 2.4 Countable Sets: Implications as 2.5 Kolmogorov's Axioms 2.6 Reliability: Series Versus Parallel Networks Problems
5 3 Random Variables and Models Derived From Classical Probability and Postulates 3.1 Random Variables and Probability Distributions: Discrete Uniform Example 3.2 The Univariate Probability Density Function: Continuous Uniform Example 3.3 Summary Statistics: Central and Non‐Central Moments 3.4 Binomial Experiments 3.5 Waiting Time for a Success: Geometric PMF 3.6 Waiting Time for Successes: Negative Binomial 3.7 Poisson Process and Distribution 3.8 Waiting Time for Poisson Events: Negative Exponential PDF 3.9 The Normal Distribution (Also Known as the Gaussian Distribution) Problems
6 4 Bivariate Random Variables, Transformations, and Simulations 4.1 Bivariate Continuous Random Variables 4.2 Change of Variables 4.3 Simulations Problems
7 5 Approximations and Asymptotics 5.1 Why Do We Like Random Samples? 5.2 Useful Inequalities 5.3 Sequences of Random Variables 5.4 Central Limit Theorem 5.5 Delta Method and Variance‐stabilizing Transformations Problems Notes
8 6 Parameter Estimation 6.1 Desirable Properties of an Estimator 6.2 Moments of the Sample Mean and Variance 6.3 Method of Moments (MoM) 6.4 Sufficient Statistics and Data Compression 6.5 Bayesian Parameter Estimation 6.6 Maximum Likelihood Parameter Estimation 6.7 Information Inequalities and the Cramér–Rao Lower Bound Problems
9 7 Hypothesis Testing 7.1 Setting up a Hypothesis Test 7.2 Best Critical Region for Simple Hypotheses 7.3 Best Critical Region for a Composite Alternative Hypothesis 7.4 Reporting Results: ‐values and Power 7.5 Multiple Testing and the Bonferroni Correction Problems
10 8 Confidence Intervals and Other Hypothesis Tests 8.1 Confidence Intervals 8.2 Hypotheses About the Variance and the ‐Distribution 8.3 Pearson's Chi‐Squared Tests 8.4 Correlation Coefficient Tests and CIs 8.5 Linear Regression 8.6 Analysis of Variance Problems
11 9 Topics in Statistics 9.1 MSE and Histogram Bin Width Selection 9.2 An Optimal Stopping Time Problem 9.3 Compound Random Variables 9.4 Simulation and the Bootstrap 9.5 Multiple Linear Regression 9.6 Experimental Design 9.7 Logistic Regression, Poisson Regression, and the Generalized Linear Model 9.8 Robustness 9.9 Conclusions
12 Appendices A Notation Used in This Book B Common Distributions C Using R and Mathematica For This Text
13 Bibliography
14 Index
15 End User License Agreement
1 Chapter 1 Table 1.1 Lord Rayleigh's 24 measurements (sorted) of the weight of a sample ...
2 Chapter 3Table 3.1 Probabilities for roll of a single die.Table 3.2 The 36 equally likely simple outcomes when rolling a pair of dice.Table 3.3 Probability distribution function for the sum of pips on two dice.
3 Chapter 7Table 7.1 Truth table for hypothesis testing.Table 7.2 Upper critical values for the two‐sided 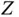 ‐test versus
‐test versus 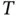 ‐test.
‐test.
4 Chapter 8Table 8.1 Data for testing the adequacy of a normal model.Table 8.2 Contingency table for Scottish children.Table 8.3 Expected values assuming independence of sex and hair color.
1 Chapter 1 Figure 1.1 Displays of the father–son height data collected by Karl Pearson:... Figure 1.2 Histograms of the sons' heights (top row) and fathers' heights (b... Figure 1.3 Displays of Lord Rayleigh's 24 measurements of the atomic weight ... Figure 1.4 Scatter diagrams of the raw and 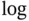 ‐transformed body and brain weig... Figure 1.5 Analysis of the number of O‐ring failures for the first 24 Space ... Figure 1.6 Father–son height data collected by Karl Pearson. Figure 1.7 Box–Cox transformation on natural and log scales.
‐transformed body and brain weig... Figure 1.5 Analysis of the number of O‐ring failures for the first 24 Space ... Figure 1.6 Father–son height data collected by Karl Pearson. Figure 1.7 Box–Cox transformation on natural and log scales.
2 Chapter 2 Figure 2.1 (Left) Venn diagram of the classical probability experiment rolli... Figure 2.2 Four possible relationships between events 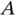 and
and 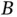 . Figure 2.3 Probability that
. Figure 2.3 Probability that 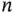 students all have different birthdays, plotted... Figure 2.4 (Left) Venn diagram of partition of
students all have different birthdays, plotted... Figure 2.4 (Left) Venn diagram of partition of 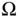 into
into 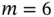 sets
sets 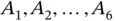 ; (middle) set... Figure 2.5 Illustration of the FPC. Select one of
; (middle) set... Figure 2.5 Illustration of the FPC. Select one of 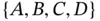 , then one of
, then one of 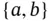 , and fina...Figure 2.6 A series network (left) and parallel network (right) of
, and fina...Figure 2.6 A series network (left) and parallel network (right) of 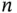 compone...
compone...
3 Chapter 3Figure 3.1 (Left) The cumulative distribution function for the roll of a sin...Figure 3.2 (Left) The cumulative distribution function for the sum of pips o...Figure 3.3 (Left) The CDF for a 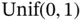 density; and (right) its PDF.Figure 3.4 The shaded areas give the probabilities of the events
density; and (right) its PDF.Figure 3.4 The shaded areas give the probabilities of the events 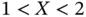 ,
, 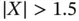 , and
, and 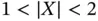 Figure 3.5 The CDF and PDF of an isosceles triangular distribution.Figure 3.6 Binomial PMF for various combinations of
Figure 3.5 The CDF and PDF of an isosceles triangular distribution.Figure 3.6 Binomial PMF for various combinations of 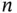 and
and 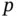 .Figure 3.7 Binomial CDF for
.Figure 3.7 Binomial CDF for 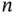 and
and 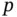 as in Figure 3.6.Figure 3.8 The two disjoint events that result in
as in Figure 3.6.Figure 3.8 The two disjoint events that result in 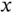 calls in
calls in 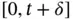 , ignoring the...Figure 3.9 Examples of the Poisson PMF, where
, ignoring the...Figure 3.9 Examples of the Poisson PMF, where 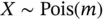 .Figure 3.10 Examples of the discrete Poisson PMF, Pois
.Figure 3.10 Examples of the discrete Poisson PMF, Pois 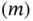 , and the continuous ...Figure 3.11 Gauss on the German Mark bill. Note the Gaussian curve.Figure 3.12 Standard normal CDF,
, and the continuous ...Figure 3.11 Gauss on the German Mark bill. Note the Gaussian curve.Figure 3.12 Standard normal CDF, 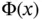 , and PDF,
, and PDF, 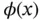 , for
, for 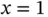 .
.
Читать дальше

 ‐test versus
‐test versus 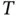 ‐test.
‐test. ‐transformed body and brain weig... Figure 1.5 Analysis of the number of O‐ring failures for the first 24 Space ... Figure 1.6 Father–son height data collected by Karl Pearson. Figure 1.7 Box–Cox transformation on natural and log scales.
‐transformed body and brain weig... Figure 1.5 Analysis of the number of O‐ring failures for the first 24 Space ... Figure 1.6 Father–son height data collected by Karl Pearson. Figure 1.7 Box–Cox transformation on natural and log scales.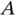 and
and 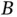 . Figure 2.3 Probability that
. Figure 2.3 Probability that 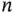 students all have different birthdays, plotted... Figure 2.4 (Left) Venn diagram of partition of
students all have different birthdays, plotted... Figure 2.4 (Left) Venn diagram of partition of 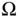 into
into 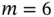 sets
sets 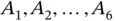 ; (middle) set... Figure 2.5 Illustration of the FPC. Select one of
; (middle) set... Figure 2.5 Illustration of the FPC. Select one of 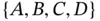 , then one of
, then one of 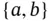 , and fina...Figure 2.6 A series network (left) and parallel network (right) of
, and fina...Figure 2.6 A series network (left) and parallel network (right) of 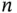 compone...
compone...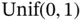 density; and (right) its PDF.Figure 3.4 The shaded areas give the probabilities of the events
density; and (right) its PDF.Figure 3.4 The shaded areas give the probabilities of the events 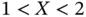 ,
, 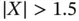 , and
, and 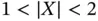 Figure 3.5 The CDF and PDF of an isosceles triangular distribution.Figure 3.6 Binomial PMF for various combinations of
Figure 3.5 The CDF and PDF of an isosceles triangular distribution.Figure 3.6 Binomial PMF for various combinations of 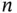 and
and 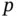 .Figure 3.7 Binomial CDF for
.Figure 3.7 Binomial CDF for 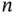 and
and 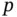 as in Figure 3.6.Figure 3.8 The two disjoint events that result in
as in Figure 3.6.Figure 3.8 The two disjoint events that result in 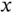 calls in
calls in 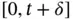 , ignoring the...Figure 3.9 Examples of the Poisson PMF, where
, ignoring the...Figure 3.9 Examples of the Poisson PMF, where 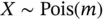 .Figure 3.10 Examples of the discrete Poisson PMF, Pois
.Figure 3.10 Examples of the discrete Poisson PMF, Pois 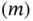 , and the continuous ...Figure 3.11 Gauss on the German Mark bill. Note the Gaussian curve.Figure 3.12 Standard normal CDF,
, and the continuous ...Figure 3.11 Gauss on the German Mark bill. Note the Gaussian curve.Figure 3.12 Standard normal CDF, 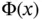 , and PDF,
, and PDF, 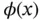 , for
, for 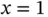 .
.










