There are two basic tasks for the statistician. First is to characterize the distribution of possible outcomes using a batch of representative data. An actuary may be asked to find a dollar loss for car accidents that is not exceeded 99.999% of the time. An economist may be asked to provide useful summaries of a collection of income data. The histogram is our primary tool here, an idea that did not appear until the 17th century; see Graunt (1662), who analyzed death records during height of the plague outbreak in Europe.
The second task is that of prediction. A bank may wish to understand how credit risk is related to other information that may be available. A mechanical engineer may wish to understand the risk inherent in a new design under extreme conditions. Methods for performing this task underlie many algorithms today, for example, translating foreign languages or image recognition.
The mathematical backbone of all of our statistical methods is probability theory. Thus we study the basics of probability theory and random variables in the first part of this course. Statistical methods and the basics of statistical decision theory form the core of the middle third of this course. Specific tests and data analysis approaches finish our study.
1.1 Exploring the Distribution of Data
Tukey (1977) introduced a number of data summaries in his book Exploratory Data Analysis . Many are based on quantiles or percentiles of the data vector. Percentiles are particular choices of the sorted data. The middlemost is the median, or the 50th percentile. As a measure of spread, Tukey focused on the distance from the 25th to the 75th percentiles, the so‐called interquartile range (IQR). A three‐point summary would list these percentiles. Instead Tukey popularized the box‐and‐whiskers plot, which is a five‐point summary. The additional two points are intended to capture 99% of the data. These are drawn at a distance of 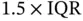 from the two quartiles. Any points outside these whiskers are plotted as potential outliers .
from the two quartiles. Any points outside these whiskers are plotted as potential outliers .
1.1.1 Pearson's Father–Son Height Data
We illustrate these ideas on a set of data collected by Karl Pearson over a century ago. He recorded the heights of 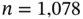 fathers and an adult son. In the left frame in Figure 1.1, we display a box‐and‐whiskers plot of these data. We see that the sons are taller than their fathers by about an inch. There are also more potential outliers among the sons for some reason.
fathers and an adult son. In the left frame in Figure 1.1, we display a box‐and‐whiskers plot of these data. We see that the sons are taller than their fathers by about an inch. There are also more potential outliers among the sons for some reason.
In the middle frame of Figure 1.1, we show Tukey's stem‐and‐leaf plot of the 1078 differences of the heights of each son and his father. The range of the data is 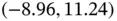 and the first seven sorted values rounded to one decimal place are
and the first seven sorted values rounded to one decimal place are 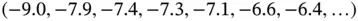 . Each data point is decomposed into a stem and a leaf digit. Thus
. Each data point is decomposed into a stem and a leaf digit. Thus 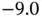 has a stem of
has a stem of 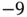 and a leaf of 0. The top line is actually
and a leaf of 0. The top line is actually  , although it is too small to see. With so much data, each stem is broken into two lines to provide more detail. Thus the next two lines show a stem of
, although it is too small to see. With so much data, each stem is broken into two lines to provide more detail. Thus the next two lines show a stem of 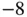 but no leaves
but no leaves  twice. The fourth line shows
twice. The fourth line shows  and the fifth line reads
and the fifth line reads  and so on. This figure was generated using the
and so on. This figure was generated using the 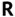 command
command  ; RCore Team (2018). (The default
; RCore Team (2018). (The default 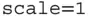 has half as many stems.) Thus the stem‐and‐leaf plot shows the frequency count of points for each stem as character strings.
has half as many stems.) Thus the stem‐and‐leaf plot shows the frequency count of points for each stem as character strings.
In the right frame of Figure 1.1, we show the frequency counts in a histogram. The histogram uses a parameter 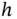 called the bin width to construct an equally spaced mesh
called the bin width to construct an equally spaced mesh 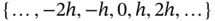 . Then we count the number of points in each interval. These counts are displayed as a bar chart. (The histogram can use any anchor point, although 0 is a common choice.) For the histogram shown, the anchor point selected was 0, and
. Then we count the number of points in each interval. These counts are displayed as a bar chart. (The histogram can use any anchor point, although 0 is a common choice.) For the histogram shown, the anchor point selected was 0, and 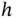 was chosen using Scott's rule
was chosen using Scott's rule 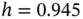 ; see Scott (1979). This rule is discussed in Section 9.1.4.1. The default choice in
; see Scott (1979). This rule is discussed in Section 9.1.4.1. The default choice in 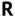 function
function histis Sturges' rule, discussed in Section 9.1.4.3, which chooses 11 bins with 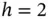 (not shown).
(not shown).
The choice of 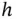 is often considered a matter of convenience. The stem‐and‐leaf plot using one‐digit integer stems limits its choices. By way of contrast, any positive real number
is often considered a matter of convenience. The stem‐and‐leaf plot using one‐digit integer stems limits its choices. By way of contrast, any positive real number 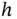 can be used in a histogram. In Figure 1.2, we show the histograms using
can be used in a histogram. In Figure 1.2, we show the histograms using 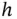 by Scott's rule, as well as
by Scott's rule, as well as 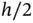 and
and 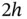 . Loosely speaking, the histograms using
. Loosely speaking, the histograms using 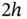 are missing useful information, while the histograms using
are missing useful information, while the histograms using 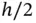 display spurious detail. We discuss strategies for finding the best choice of
display spurious detail. We discuss strategies for finding the best choice of 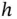 in Section 9.1. In any case, the histogram is a powerful tool for understanding the full distribution of data.
in Section 9.1. In any case, the histogram is a powerful tool for understanding the full distribution of data.
Читать дальше

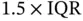 from the two quartiles. Any points outside these whiskers are plotted as potential outliers .
from the two quartiles. Any points outside these whiskers are plotted as potential outliers .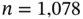 fathers and an adult son. In the left frame in Figure 1.1, we display a box‐and‐whiskers plot of these data. We see that the sons are taller than their fathers by about an inch. There are also more potential outliers among the sons for some reason.
fathers and an adult son. In the left frame in Figure 1.1, we display a box‐and‐whiskers plot of these data. We see that the sons are taller than their fathers by about an inch. There are also more potential outliers among the sons for some reason.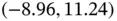 and the first seven sorted values rounded to one decimal place are
and the first seven sorted values rounded to one decimal place are 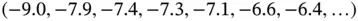 . Each data point is decomposed into a stem and a leaf digit. Thus
. Each data point is decomposed into a stem and a leaf digit. Thus 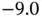 has a stem of
has a stem of 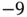 and a leaf of 0. The top line is actually
and a leaf of 0. The top line is actually  , although it is too small to see. With so much data, each stem is broken into two lines to provide more detail. Thus the next two lines show a stem of
, although it is too small to see. With so much data, each stem is broken into two lines to provide more detail. Thus the next two lines show a stem of 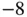 but no leaves
but no leaves  twice. The fourth line shows
twice. The fourth line shows  and the fifth line reads
and the fifth line reads  and so on. This figure was generated using the
and so on. This figure was generated using the 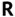 command
command  ; RCore Team (2018). (The default
; RCore Team (2018). (The default 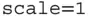 has half as many stems.) Thus the stem‐and‐leaf plot shows the frequency count of points for each stem as character strings.
has half as many stems.) Thus the stem‐and‐leaf plot shows the frequency count of points for each stem as character strings.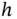 called the bin width to construct an equally spaced mesh
called the bin width to construct an equally spaced mesh 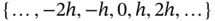 . Then we count the number of points in each interval. These counts are displayed as a bar chart. (The histogram can use any anchor point, although 0 is a common choice.) For the histogram shown, the anchor point selected was 0, and
. Then we count the number of points in each interval. These counts are displayed as a bar chart. (The histogram can use any anchor point, although 0 is a common choice.) For the histogram shown, the anchor point selected was 0, and 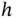 was chosen using Scott's rule
was chosen using Scott's rule 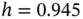 ; see Scott (1979). This rule is discussed in Section 9.1.4.1. The default choice in
; see Scott (1979). This rule is discussed in Section 9.1.4.1. The default choice in 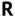 function
function 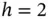 (not shown).
(not shown).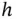 is often considered a matter of convenience. The stem‐and‐leaf plot using one‐digit integer stems limits its choices. By way of contrast, any positive real number
is often considered a matter of convenience. The stem‐and‐leaf plot using one‐digit integer stems limits its choices. By way of contrast, any positive real number 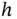 can be used in a histogram. In Figure 1.2, we show the histograms using
can be used in a histogram. In Figure 1.2, we show the histograms using 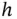 by Scott's rule, as well as
by Scott's rule, as well as 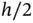 and
and 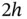 . Loosely speaking, the histograms using
. Loosely speaking, the histograms using 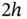 are missing useful information, while the histograms using
are missing useful information, while the histograms using 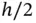 display spurious detail. We discuss strategies for finding the best choice of
display spurious detail. We discuss strategies for finding the best choice of 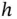 in Section 9.1. In any case, the histogram is a powerful tool for understanding the full distribution of data.
in Section 9.1. In any case, the histogram is a powerful tool for understanding the full distribution of data.










