1 ...8 9 10 12 13 14 ...26
Measures of Location – The Three ‘Ms’ – Mean, Median and Mode
Mean or Average
The arithmetic mean or average of n observations 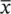 (pronounced x bar) is simply the sum of the observations divided by their number; thus
(pronounced x bar) is simply the sum of the observations divided by their number; thus
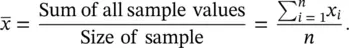
In the above equation, x irepresents the individual sample values and 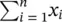 their sum. The Greek letter ‘∑’ (sigma) is the Greek capital ‘S’ and stands for ‘sum’ and simply means ‘add up the n observations x ifrom the first to the last ( n th)’.
their sum. The Greek letter ‘∑’ (sigma) is the Greek capital ‘S’ and stands for ‘sum’ and simply means ‘add up the n observations x ifrom the first to the last ( n th)’.
Example – Calculation of the Mean – Corn Size Data (mm)
In the randomised controlled trial that investigated the effectiveness of salicylic acid plasters compared with usual scalpel debridement for treatment of foot corns (Farndon et al. 2013), the baseline size of the index corn (at its widest diameter in mm) was measured by an independent podiatrist (foot specialist) who was not involved in the subsequent treatment of the patients. Consider the following 16 baseline corn sizes in mm, listed in ascending order, selected randomly from the 200 patients, with valid baseline corn size data, in the trial.
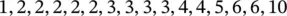
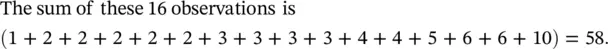
Thus, the mean 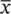 = 58/16 = 3.625 mm or 3.6 mm. It is usual to quote one more decimal place for the mean than the data recorded.
= 58/16 = 3.625 mm or 3.6 mm. It is usual to quote one more decimal place for the mean than the data recorded.
The major advantage of the mean is that it uses all the data values and is, in a statistical sense, therefore efficient. The mean also characterises some important statistical distributions to be discussed in Chapter 4. The main disadvantage of the mean is that it is vulnerable to what are known as outliers. Outliers are single observations that, if excluded from the calculations, have noticeable influence on the results. For example, if we had entered ‘100 mm’ instead of ‘10 mm’, for the 16th patient, in the calculation of the mean, we would find the mean changed from 3.6 to 9.3 mm. It does not necessarily follow, however, that outliers should be excluded from the final data summary, or that they result from an erroneous measurement.
If the data are binary, that is nominal and are coded 0 or 1, then 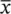 is the proportion of individuals with value 1, and this can also be expressed as a percentage. In the foot corn plaster trial, the corn had healed or resolved by a three‐month follow‐up in 52 out of 189 patients. If whether the corn was healed at a three‐month post‐randomisation follow‐up is coded as a ‘1’ for ‘yes, healed’, and a ‘0’ for ‘no, not healed’, then the mean of this variable is 0.257 or 25.7%.
is the proportion of individuals with value 1, and this can also be expressed as a percentage. In the foot corn plaster trial, the corn had healed or resolved by a three‐month follow‐up in 52 out of 189 patients. If whether the corn was healed at a three‐month post‐randomisation follow‐up is coded as a ‘1’ for ‘yes, healed’, and a ‘0’ for ‘no, not healed’, then the mean of this variable is 0.257 or 25.7%.
The median is estimated by first ordering the data from smallest to largest, and then counting upwards for half the observations. The estimate of the median is either the observation at the centre of the ordering in the case of an odd number of observations, or the simple average of the middle two observations if the total number of observations is even.
Example – Calculation of the Median – Corn Size Data
Consider the following 16 corn sizes in millimetres selected randomly from the Farndon (2013) study. We order the 16 observations from smallest to largest (See Table 2.4); the median is the middle observation which splits the data set into two halves with equal number of observations in each half (eight in this example). As the number if observations are even ( n = 16); the median is the average of the two central ordered values (the eighth and ninth). So, the median corn size is (3 + 3)/2 = 3 mm.
If we had observed an additional 17th subject with a corn size of 10 mm the median would be the 9th ordered observation, which is 3 mm.
The median has the advantage that it is not affected by outliers, so for example the median in the data would be unaffected by replacing largest corn size of ‘10 mm’ with ‘100 mm’. However, it is not statistically efficient, as it does not make use of all the individual data values.
A third measure of location is termed the mode. This is the value that occurs most frequently, or, if the data are grouped, the grouping with the highest frequency. It is not used much in statistical analysis, since its value depends on the accuracy with which the data are measured; although it may be useful for categorical data to describe the most frequent category. However, the expression ‘bimodal’ distribution is used to describe a distribution with two peaks in it. This can be caused by mixing two or more populations together. For example, height might appear to have a bimodal distribution if one had men and women in the study population. Some illnesses may raise a biochemical measure, so in a population containing healthy individuals and those who are ill one might expect a bimodal distribution. However, some illnesses are defined by the measure of, say obesity or high blood pressure, and in these cases the distributions are usually unimodal with those above a given value regarded as ill .
Table 2.4 The 16 corn sizes ordered and ranked from smallest to largest.
| Rank order |
Corn size (mm) |
|
| 1 |
1 |
|
| 2 |
2 |
|
| 3 |
2 |
|
| 4 |
2 |
|
| 5 |
2 |
|
| 6 |
2 |
|
| 7 |
3 |
|
| 8 |
3 |
 |
| 9 |
3 |
| 10 |
3 |
|
| 11 |
4 |
|
| 12 |
4 |
|
| 13 |
5 |
|
| 14 |
6 |
|
| 15 |
6 |
|
| 16 |
10 |
|
Example – Calculation of the Mode – Corn Size Data
In the 16 patients with corns; 5 patients have a corn size of 2 mm; thus, the modal corn size is 2 mm.
Measures of Dispersion or Variability
We also need a numerical way of summarising the amount of spread or variability in a data set. The three main approaches to quantifying variability are: the range; interquartile range and the standard deviation.
The simplest way to describe the spread of a data set is to quote the minimum (lowest) and maximum (highest) values. The range is given as the smallest and largest observations. For some data it is very useful, because one would want to know these numbers, for example in a sample the age of the youngest and oldest participant. However, if outliers are present it may give a distorted impression of the variability of the data, since only two of the data points are included in making the estimate. Thus, the range is affected by extreme values at each end of the data.
Читать дальше

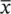 (pronounced x bar) is simply the sum of the observations divided by their number; thus
(pronounced x bar) is simply the sum of the observations divided by their number; thus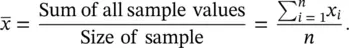
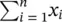 their sum. The Greek letter ‘∑’ (sigma) is the Greek capital ‘S’ and stands for ‘sum’ and simply means ‘add up the n observations x ifrom the first to the last ( n th)’.
their sum. The Greek letter ‘∑’ (sigma) is the Greek capital ‘S’ and stands for ‘sum’ and simply means ‘add up the n observations x ifrom the first to the last ( n th)’.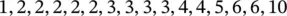
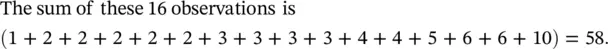
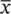 = 58/16 = 3.625 mm or 3.6 mm. It is usual to quote one more decimal place for the mean than the data recorded.
= 58/16 = 3.625 mm or 3.6 mm. It is usual to quote one more decimal place for the mean than the data recorded.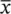 is the proportion of individuals with value 1, and this can also be expressed as a percentage. In the foot corn plaster trial, the corn had healed or resolved by a three‐month follow‐up in 52 out of 189 patients. If whether the corn was healed at a three‐month post‐randomisation follow‐up is coded as a ‘1’ for ‘yes, healed’, and a ‘0’ for ‘no, not healed’, then the mean of this variable is 0.257 or 25.7%.
is the proportion of individuals with value 1, and this can also be expressed as a percentage. In the foot corn plaster trial, the corn had healed or resolved by a three‐month follow‐up in 52 out of 189 patients. If whether the corn was healed at a three‐month post‐randomisation follow‐up is coded as a ‘1’ for ‘yes, healed’, and a ‘0’ for ‘no, not healed’, then the mean of this variable is 0.257 or 25.7%.











