We can formulate the following rule of indeterminate Lagrange multipliers for solving constrained optimization problems with equality constraints:
1 1) Write the Lagrange function
2 2) Write the necessary conditions for the extremum of the function L, that is:
3 3) Find the stationary points, that is, the solutions of these equations, provided that not all Lagrange multipliers λ0, λ1, … , λm are zero.
4 4) Find a solution to the problem among the stationary points or prove that the problem has no solutions.
1.4.2. Problems with equality and inequality constraints
Let fi : ℝ n→ ℝ be differentiable functions of n real variables. The constrained optimization problem with equality and inequality constraints is the following problem:
[1.3] 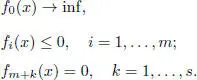
We will formulate the necessary conditions for solution of the problem [1.3].
THEOREM 1.19.– ( Theorem on indeterminate Lagrange multipliers ) Let  be a point of local solution of the problem [1.3], and let the functions fi ( x ), i = 0, … , m + s , be continuously differentiable in some neighborhood U of the point
be a point of local solution of the problem [1.3], and let the functions fi ( x ), i = 0, … , m + s , be continuously differentiable in some neighborhood U of the point  . Then there will exist the Lagrange multipliers λ 0, λ 1, … , λ m+s, not all equal to zero, such that for the Lagrange function
. Then there will exist the Lagrange multipliers λ 0, λ 1, … , λ m+s, not all equal to zero, such that for the Lagrange function

the following conditions hold true:
– stationarity condition with respect to x
– complementary slackness condition
– non-negativity condition
Consequently, the rule of indeterminate Lagrange multipliers for solving constrained optimization problems with equality and inequality constraints is as follows:
1 1) Write the Lagrange function
2 2) Write the necessary conditions:– stationarity condition– complementary slackness condition– non-negativity condition
3 3) Find the critical points, that is, all admissible points that satisfy the necessary conditions with the Lagrange multiplier λ0 = 0 and λ0 ≠ 0.
4 4) Find a solution to the problem among the stationary points or prove that the problem has no solutions.
REMARK 1.1.– Using the rule of indeterminate Lagrange multipliers for solving constrained optimization problems with equality constraints, one can choose the number λ 0as both positive and negative. For constrained optimization problems with equality and inequality constraints, the sign of λ 0is significant.
EXAMPLE 1.2.– Solve the constrained optimization problem

The only obvious solution to this problem is the point 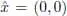 . We solve the problem by the Lagrange method.
. We solve the problem by the Lagrange method.
1 1) Write the Lagrange function .
2 2) Write the stationary equations
3 3) If λ0 = 1, we get the equationsThe first equation is incompatible with the condition . Therefore, the system of equationshas no solutions.
4 4) If λ0 = 0, then x1 = 0, x2 = 0 is a solution of the system of equations.
Answer . (0, 0) ∈ absmin.
Example 1.2 shows that by applying the rule of indeterminate Lagrange multipliers, it is not always possible to take λ 0= 1.
EXAMPLE 1.3.– Solve the constrained optimization problem
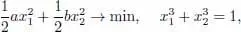
where a > 0 and b > 0 are given numbers.
Solution .
1 1) Write out the (regular) Lagrange function (as indicated in theorem 1.15 the regularity condition is satisfied here):
2 2) Since
the system of equations for determination of stationary points has the form:

This system of equations has three solutions:

1 3) Next we have
For the three solutions found, this matrix takes the form accordingly

The condition  , i = 1, … , m , here is of the form
, i = 1, … , m , here is of the form  . For the first two solutions, this means that h 2= 0 and h 1= 0, respectively. It is clear from this that matrices A 1and A 2satisfy the conditions of theorem 1.17 (although they are not positive definite). Therefore, the points (0, 1), (1, 0) are strict local solutions of the problem. For the matrix, A 3conditions of theorem 1.17 are not satisfied. That is why the point
. For the first two solutions, this means that h 2= 0 and h 1= 0, respectively. It is clear from this that matrices A 1and A 2satisfy the conditions of theorem 1.17 (although they are not positive definite). Therefore, the points (0, 1), (1, 0) are strict local solutions of the problem. For the matrix, A 3conditions of theorem 1.17 are not satisfied. That is why the point

cannot be a solution of the minimization problem. This point is a local solution of the maximization problem of the same function under the same restrictions.
Answer .  ∈ locmin,
∈ locmin,  ∈ locmin,
∈ locmin,

EXAMPLE 1.4.– Solve the constrained optimization problem

Solution.
1 1) Write out the Lagrange function
2 2) Write the necessary conditions:– stationarity condition– complementary slackness condition– non-negativity condition λ0 ≥ 0, λ1 ≥ 0.
3 3) If λ0 = 0, then, in accordance with the condition of stationarity we have λ1 = 0, and λ2 = 0. So all Lagrange multipliers are zero. This contradicts the conditions of the Lagrange theorem 1.19. Take λ0 = 1/2. Let λ1 ≠ 0. Then, under the complementary slackness condition we have 2x1 – x2 + x3 – 5 = 0. We express x1, x2, x3 through λ1, λ2 and substitute into the equationWe get λ1 = –9/14 < 0. This contradicts the non-negativity condition. Let λ1 = 0, then x1 = x2 = x3 = 1 is a critical point.
Читать дальше

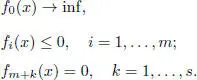
 be a point of local solution of the problem [1.3], and let the functions fi ( x ), i = 0, … , m + s , be continuously differentiable in some neighborhood U of the point
be a point of local solution of the problem [1.3], and let the functions fi ( x ), i = 0, … , m + s , be continuously differentiable in some neighborhood U of the point 

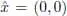 . We solve the problem by the Lagrange method.
. We solve the problem by the Lagrange method.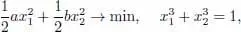



 , i = 1, … , m , here is of the form
, i = 1, … , m , here is of the form  . For the first two solutions, this means that h 2= 0 and h 1= 0, respectively. It is clear from this that matrices A 1and A 2satisfy the conditions of theorem 1.17 (although they are not positive definite). Therefore, the points (0, 1), (1, 0) are strict local solutions of the problem. For the matrix, A 3conditions of theorem 1.17 are not satisfied. That is why the point
. For the first two solutions, this means that h 2= 0 and h 1= 0, respectively. It is clear from this that matrices A 1and A 2satisfy the conditions of theorem 1.17 (although they are not positive definite). Therefore, the points (0, 1), (1, 0) are strict local solutions of the problem. For the matrix, A 3conditions of theorem 1.17 are not satisfied. That is why the point
 ∈ locmin,
∈ locmin,  ∈ locmin,
∈ locmin,












