1 1) x1 = 0, x2 = 1, bλ0 + 3λ1 − 2λ2 = 0, λ1 ≥ 0, λ2 ≥ 0, (λ1, λ2) ≠ 0;
2 2) x1 = 0, x2 = −1, bλ0 − 2λ2 = 0, λ1 = 0, λ2 > 0.
Similarly, assuming that x 2= 0, we obtain two other groups of solutions:
1 3) x1 = 1, x2 = 0, aλ0 + 3λ1 − 2λ2 = 0, λ1 ≥ 0, λ2 ≥ 0, (λ1, λ2) ≠ 0;
2 4) x1 = −1, x2 = 0, aλ0 − 2λ2 = 0, λ1 = 0, λ2 > 0.
Assume that x 1≠ 0, x 2≠ 0. Then equations of the system can be presented in the form

If here λ 1= 0, then λ 0= 0, since a ≠ b . But then λ 2= 0, which contradicts the system of conditions. It remains to be assumed that λ 1> 0. Then 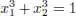 . Given that λ 1≠ 0, λ 2≠ 0, we deduce from this that
. Given that λ 1≠ 0, λ 2≠ 0, we deduce from this that 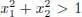 , and therefore λ 2= 0. Now we can easily get another group of solutions of the system:
, and therefore λ 2= 0. Now we can easily get another group of solutions of the system:
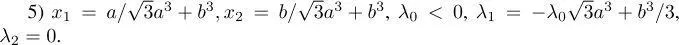
Note that in (1) and (3) the multiplier λ 0can accept both positive and negative values, in (2) and (4) it can accept only positive values and in (5) it can accept only negative values. Therefore, (0, 1) and (1, 0) are stationary points both in the minimization problem and in the maximization problem, (0, –1) and (–1, 0) are stationary points only in the minimization problem, and the point of (5) is the stationary point only in the problem of maximization.
Now we will study the stationary points for optimality. The function f is strongly convex on ℝ 2. Therefore, it reaches the global minimum on any closed set X . We calculate the value of f at the stationary points of the minimization problem:

Since a < b , hence (1.0) and (–1.0) are points of the global minimum of the function f on X .
Let us represent the function f in the form
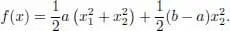
If we move from the points (0, 1) and (0, –1), remaining on the circle 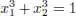 , and hence in X , then the value of f will decrease. Consequently, these points are not points of the local minimum f on X . At the same time, for any ε > 0, the point (– ε , 1) belongs to X and f (0, 1) < f (– ε , 1). Therefore, the point (0, 1) is not a point of the local maximum f on X . Consequently, the stationary points (0, 1) and (0, –1) are not solutions of the problem.
, and hence in X , then the value of f will decrease. Consequently, these points are not points of the local minimum f on X . At the same time, for any ε > 0, the point (– ε , 1) belongs to X and f (0, 1) < f (– ε , 1). Therefore, the point (0, 1) is not a point of the local maximum f on X . Consequently, the stationary points (0, 1) and (0, –1) are not solutions of the problem.
We now consider the matrix of the second derivatives of the Lagrangian function:
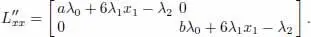
For values with (5), this matrix is as follows:
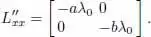
Since λ 0< 0, this matrix is positive definite. Sufficient conditions for the minimum are fulfilled. Consequently, ( 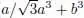 ,
, 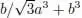 ) is the point of the strict local minimum of f on X .
) is the point of the strict local minimum of f on X .
Answer .  ∈ absmin,
∈ absmin,  ∈ absmin,
∈ absmin, 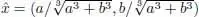 ∈ absmax. Δ
∈ absmax. Δ
Let us solve the following optimization problems.
1 1) f(x, y) = x4 + y4 − 4xy → extr.
2 2) f(x, y) = ae−x + be−y + ln(ex + ey) → extr.
3 3) f(x, y) = (x + y)(x − a)(y − b) → extr.
4 4) f(x, y) = x2 − 2xy2 + y4 − y5 → extr.
5 5) f(x, y) = x + y + 4 sin (x) sin (y) → extr.
6 6) f(x, y) = xex − (1 + ex) cos (y) → extr.
7 7) f(x, y) = (x2 + y2)e−(x2 + y2) → extr.
8 8) f(x, y) = xy ln (x2 + y2) → extr.
9 9) .
10 10) f(x, y) = sin (x) sin (y) sin(x + y) → extr, 0 ≤ x ≤ π, 0 ≤ y ≤ π.
11 11) f(x, y) = sin (x) +cos (y) +cos (x − y) → extr, 0 ≤ x ≤ π/2, 0 ≤ y ≤ π/2.
12 12) f(x, y) = x2 + xy + y2 − 4 ln (x) − 10 ln (y) → extr.
13 13) f(x, y) = (5x + 7y − 25)e−(x2 + y2 + xy) → extr.
14 14) f(x, y) = ex2−y (5 − 2x + y) → extr.
15 15) f(x, y) = e2x+3y(8x2 − 6xy + 3y2) → extr.
16 16) .
17 17) .
18 18) .
19 19) f(x, y) = 2x4 + y4 − x2 − 2y2 → extr.
20 20) f(x, y) = x2 − xy + y2 − 2x + y → extr.
21 21) f(x, y) = xy + 50/x + 20/y → extr.
22 22) f(x, y) = x2 − y2 − 4x + 6y → extr.
23 23) f(x, y) = 5x2 + 4xy + y2 − 16x − 12y → extr.
24 24) f(x, y) = 3x2 + 4xy + y2 − 8x − 12y → extr.
25 25) f(x, y) = 3xy − x2y − xy2 → extr.
26 26) f(x, y, z) = x2 + y2 + z2 − xy + x − 2z → extr.
27 27) f(x, y, z) = x2 + 2y2 + 5z2 − 2xy − 4yz − 2z → extr.
28 28) f(x, y, z) = xy2z3(a − x − 2y − 3z) → extr, a > 0.
29 29) f(x, y, z) = x3 + y2 + z2 + 12xy + 2z → extr, x > 0, y > 0, z > 0.
30 30) f(x, y, z) = x + y2/4x + z2/y + 2/z → extr.
31 31) f(x, y, z) = x2 + y2 + z2 + 2x + 4y − 6z → extr.
32 32) f(x, y) = y → extr, x3 + y3 − 3xy = 0.
33 33) f(x, y) = x3 + y3 → extr, ax + by = 1, a > 0, b > 0.
34 34) f(x, y) = x3/3 + y → extr, x2 + y2 = a, a > 0.
35 35) f(x, y) = x sin (y) → extr, 3x2 − 4 cos (y) = 1.
36 36) f(x, y) = x/a + y/b → extr, x2 + y2 = 1.
37 37) f(x, y) = x2 + y2 → extr, x/a + y/b = 1.
38 38) f(x, y) = Ax2 + 2Bxy + Cy2 → extr, x2 + y2 = 1.
39 39) f(x, y) = x2 + 12xy + 2y2 → extr, 4x2 + y2 = 25.
40 40) f(x, y) = cos2 (x) + cos2 (y) → extr, x − y = π/4.
41 41) f(x, y) = x/2 + y/3 → extr, x2 + y2 = 1.
42 42) f(x, y) = x2 + y2 → extr, 3x + 4y = 1.
43 43) f(x, y) = exy → extr, x + y = 1.
44 44) f(x, y) = 5x2 + 4xy + y2 → extr, x + y = 1.
45 45) f(x, y) = 3x2 + 4xy + y2 → extr, x + y = 1.
46 46) f(x, y, z) = xy2z3 → extr, x + y + z = 1.
47 47) f(x, y, z) = xyz → extr, x2 + y2 + z2 = 1, x + y + z = 0.
Читать дальше


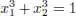 . Given that λ 1≠ 0, λ 2≠ 0, we deduce from this that
. Given that λ 1≠ 0, λ 2≠ 0, we deduce from this that 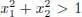 , and therefore λ 2= 0. Now we can easily get another group of solutions of the system:
, and therefore λ 2= 0. Now we can easily get another group of solutions of the system: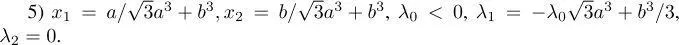

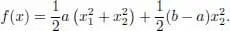
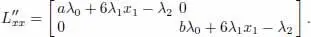
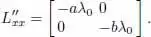
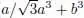 ,
, 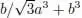 ) is the point of the strict local minimum of f on X .
) is the point of the strict local minimum of f on X . ∈ absmin,
∈ absmin,  ∈ absmin,
∈ absmin, 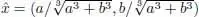 ∈ absmax. Δ
∈ absmax. Δ










