Douglas C. Montgomery - Introduction to Linear Regression Analysis

(2.39)

and a 100(1 − α ) percent CI on the intercept β 0is

(2.40)

These CIs have the usual frequentist interpretation. That is, if we were to take repeated samples of the same size at the same x levels and construct, for example, 95% CIs on the slope for each sample, then 95% of those intervals will contain the true value of β 1.

If the errors are normally and independently distributed, Appendix C.3shows that the sampling distribution of ( n − 2) MS Res/ σ 2is chi square with n − 2 degrees of freedom. Thus,

and consequently a 100(1 − α ) percent CI on σ 2is

(2.41)

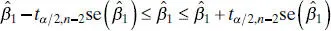
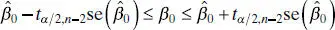
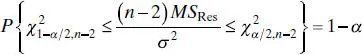
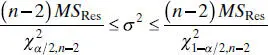
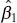We construct 95% CIs on β 1and σ 2using the rocket propellant data from Example 2.1. The standard error of is 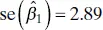and t 0.025,18= 2.101. Therefore, from Eq. (2.35), the 95% CI on the slope is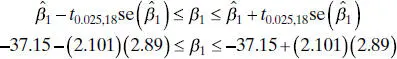

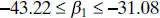
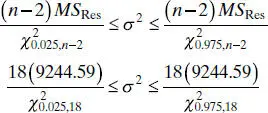
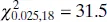or

In other words, 95% of such intervals will include the true value of the slope.

If we had chosen a different value for α , the width of the resulting CI would have been different. For example, the 90% CI on β 1is −42.16 ≤ β 1≤ −32.14, which is narrower than the 95% CI. The 99% CI is −45.49 ≤ β 1≤ 28.81, which is wider than the 95% CI. In general, the larger the confidence coefficient (1 − α ) is, the wider the CI.

The 95% CI on σ 2is found from Eq. (2.41)as follows:

From Table A.2, and 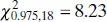. Therefore, the desired CI becomes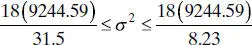

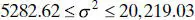
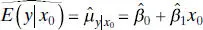
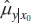or

A major use of a regression model is to estimate the mean response E ( y ) for a particular value of the regressor variable x . For example, we might wish to estimate the mean shear strength of the propellant bond in a rocket motor made from a batch of sustainer propellant that is 10 weeks old. Let x 0be the level of the regressor variable for which we wish to estimate the mean response, say E ( y | x 0). We assume that x 0is any value of the regressor variable within the range of the original data on x used to fit the model. An unbiased point estimator of E ( y | x 0) is found from the fitted model as

(2.42)

To obtain a 100(1 − α ) percent CI on E ( y | x 0), first note that is a normally distributed random variable because it is a linear combination of the observations yi . The variance of 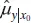is

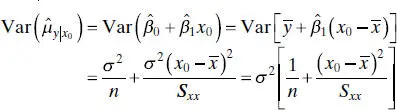
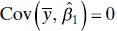since (as noted in Section 2.2.4) . Thus, the sampling distribution of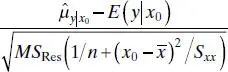

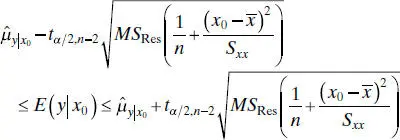
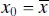is t with n − 2 degrees of freedom. Consequently, a 100(1 − α) percent CI on the mean response at the point x = x0is

(2.43)

Note that the width of the CI for E ( y | x 0) is a function of x 0. The interval width is a minimum for and widens as 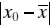increases. Intuitively this is reasonable, as we would expect our best estimates of y to be made at x values near the center of the data and the precision of estimation to deteriorate as we move to the boundary of the x space.

Consider finding a 95% CI on E ( y | x 0) for the rocket propellant data in Example 2.1. The CI is found from Eq. (2.43)as

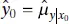If we substitute values of x 0and the fitted value at the value of x 0into this last equation, we will obtain the 95% CI on the mean response at x = x 0. For example, if 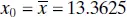, then 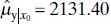, and the CI becomes