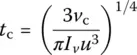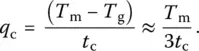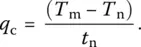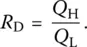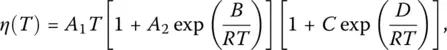where f is the interface site factor, D cthe kinetic (diffusion) coefficient, V mthe molar volume, and Δ G vthe difference in Gibbs free energy between unit volumes of the crystal and liquid.
One then obtains the critical cooling time ( t c) and rate ( q c), for a defined volume fraction of crystals v c. Taking the aforementioned value v cof 1 ppm, one obtains
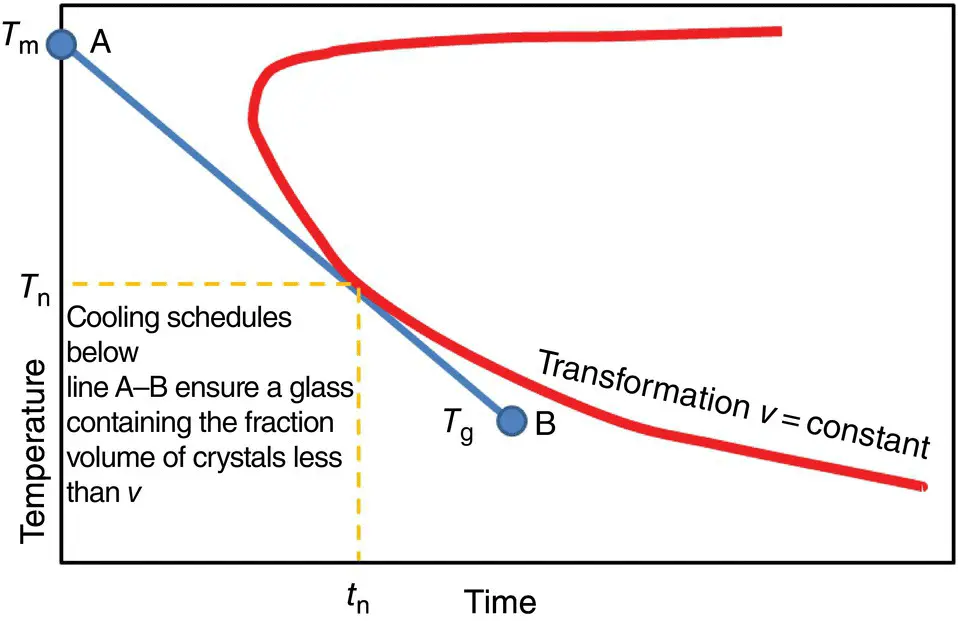
Figure 3 Determination of the critical cooling rate from a time temperature transformation diagram.
(4a) 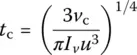
and
(4b) 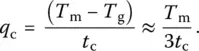
Despite its general correctness and qualitative agreement with experiments, the kinetic theory suffers from limited quantitative applications. Whereas quantitative agreement has been achieved for simple silicate systems, the discrepancy is of many orders of magnitude in most cases [6, 8].
In practice, the critical cooling rate (CCR) is determined from the so‐called time temperature transformation (TTT) diagrams, which represent nose‐shaped curves with a constant crystal fraction on time–temperature axes ( Figure 3). To ensure the obtention of a glass with a crystal volume fraction lower than v , it is required to follow a cooling pathway such that the cooling line (curve) will not touch the nose [10]. The CCR is then found as follows:
(5) 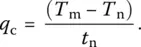
Examples are listed in Table 1.
The definition of the glass transition in terms of the standard glass transition derived from the viscosity–temperature relationship, η ( T ), is not thermodynamic, but operational [8]. As determined from changes in second‐order derivatives of thermodynamic variables, the glass transition takes place at viscosities in the range 10 8–10 13Pa s depending on the cooling rate. In view of the very steep temperature dependence of viscosity, a great difference in this parameter results in only small variations of the operational T g.
Table 1 Critical cooling rate for some glasses, K/s.
Source: After [9].
| Material |
Nucleation mechanism |
| Homogeneous |
Heterogeneous θ = 100° |
Heterogeneous θ = 60° |
Heterogeneous θ = 40° |
| SiO 2 |
9 × 10 −6 |
10 −5 |
8 × 10 −3 |
2 × 10 −1 |
| GeO 2 |
3 × 10 −3 |
3 × 10 −3 |
1 |
20 |
| Na 2O 2 SiO 2 |
6 × 10 −3 |
8 × 10 −3 |
10 |
3 × 10 2 |
| Salol [C 13H 10O 3] |
10 |
|
|
|
| Water |
10 7 |
|
|
|
| Ag |
10 10 |
|
|
|
As has long been recognized, glass formation is therefore easier in eutectic regions because freezing‐point depressions enable lower temperatures and higher viscosities to be reached [11]. However, viscosity at the liquidus is not a single scaling parameter for assessing glass‐forming ability. The temperature dependence of the viscosity below T mmust also be considered because vitrification takes place much below the liquidus [6, 8].
Viscous flow in glass‐forming liquids is characterized by deviations from Arrhenius laws with an activation energy Q that decreases from a high Q Hnear the glass transition to a low Q Lat superliquidus temperatures. As a fragility index characterizing the temperature dependence of viscosity, Doremus [12] has proposed the ratio:
(6) 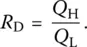
Short (or fragile) and long (or strong) glass melts are, therefore, characterized by R Dvalues higher and lower than 2, respectively.
Many equations have been proposed to express viscosity–temperature relationships ( Chapter 4.1, [13–15]). Consistent with Doremus criterion, an exponential expression with activation energies Q Land Q Hat low and high temperatures, respectively, [13] will be used here because it results from the configuron percolation theory (CPT), which accounts for viscous flow in terms of elementary excitations resulting from broken bonds named configurons [14, 16]. This equation (Sheffield model) is
( 7) 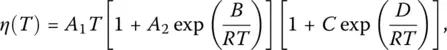
where A 1= k /6 πrD 0, A 2= exp(− S m/ R ), B = H m, C = exp(− S d/ R ) and D = H d, R the gas constant, k Boltzmann constant, r the configuron radius D 0= fgλ 2 zp 0 ν 0, f the correlation factor, g a geometrical factor (~1/6), λ the average jump length, ν 0the configuron vibrational frequency or the frequency (with which the configuron attempts to surmount the energy barrier to jump into a neighboring site), z the number of nearest neighbors, p 0a configuration factor, H dthe enthalpy, S dthe entropy of formation, and H mand S mthe enthalpy and entropy of motion of the configurons.
In practice, one finds that A 2exp( B / RT ) > > 1, i.e. that four parameters usually suffice for Eq. (7)to be fitted to practically all available experimental viscosity data [17]. Comparison with other viscosity models and numerical calculations have confirmed the excellent description of the viscosity provided by Eq. (7)for simple and complex organic and inorganic compositions (e.g. [13]). This equation can be readily approximated within narrow temperature intervals by expressions derived from the well‐known Vogel‐Tammann‐Fulcher, Adam–Gibbs, Avramov–Milchev, or Sanditov models [14, 15, 17]. It can be used at all temperatures and gives the correct Arrhenius‐type asymptotes at high and low temperatures, namely η ( T ) ~ exp( Q H/ RT ) at T << T g, and η ( T ) ~ exp( Q L/ RT ) at T >> T g, where Q H= H d+ H mand Q L= H m. Obviously, the activation energy of viscosity reduces to a low value equal to H mat high temperatures when temperature fluctuations create plenty of configurons. In contrast, some bonds need to be broken in the glassy state as temperature fluctuations do not create them effectively so that the activation energy then takes its full value Q H= H d+ H m.
Apart from inhomogeneities and potential phase separation, glasses lack long‐range order but do possess short‐ and medium‐range ordering ( Chapter 2.1). A number of models have aimed at revealing the most characteristic structural aspects of good glass formers. The most noted structural criterion for ready glass formation, i.e. at rates q clower than 10 K/s, is based on Zachariasen theory in which the oxide glasses A mO nare assumed to be 3‐D networks obeying four rules: (i) the oxygen is linked to two atoms of A; (ii) the oxygen coordination number around A is three or four; (iii) the cation polyhedra share corners; and (iv) at least three corners are shared [18]. This theory is referred to as crystallochemical, but was applicable only to oxide glasses in its original form; it led to the so‐called 3‐D continuous random network (CRN) model ( Chapter 2.1). With respect to a glass and its isochemical crystal, the basic postulates of CRN are that: (i) interatomic forces are similar in both phases; (ii) the glass is in a slightly higher energy state; (iii) nearest‐neighbor coordination polyhedra are similar; and (iv) the nature of interatomic bonds is also similar.
Читать дальше