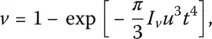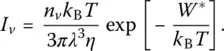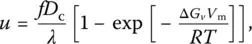Specifically, a glass has a topologically disordered distribution of atoms or molecules, like a liquid, but it has also the elastic properties of an isotropic solid. Moreover, the translation‐rotation symmetry at T gis unchanged as the glass retains the topological disorder of the fluid from which it formed. This symmetry similarity of both liquid and glassy phases generally leaves unexplained the basic differences observed between their properties. An exception is the qualitative difference that has been demonstrated in the symmetries of liquid and glasses in terms of Hausdorff dimensionality for the system of bonds which shows a stepwise change exactly at T g[3]. The reason is that broken bonds in glasses are present as point defects, thus forming a set of zero‐Hausdorff dimensionality, whereas in liquids just above the T gthey are associated in macroscopic percolating clusters that form sets characterized by the Hausdorff dimensionality ≈2.5 [3].
Although glasses are metastable materials with respect to isochemical crystals, their transformation to a thermodynamically stable crystalline structure is kinetically impeded. The metastability of silicate glasses commonly produced industrially is not a practical concern as most of them are stable for times much longer than any imaginable timescales of use. In practice, that there is no stress relaxation at room temperatures is indicated by the fact that high permanent internal stresses are preserved in glass articles made more than several millennia ago, and even in billion‐year‐old extraterrestrial glasses ( Chapter 7.1).
The reason for this stability is that relaxation processes are controlled by viscosity. The characteristic time τ required to achieve time‐independent parameters can be derived from Maxwell's simple relaxation model, which predicts that τ = η / G , where G is the shear modulus and η the viscosity ( Chapter 3.7). The higher the viscosity, the longer the relaxation time. Besides, viscosity changes are thermally activated. Glass‐forming oxides are characterized by high activation energies and very high viscosities under normal conditions. As an extreme example, fused silica has an activation energy for viscous flow of Q Hof 759 kJ/mol at lower temperatures and a shear modus of about 31 GPa, which implies relaxation times τ Mas long as 10 98years at room temperature, an immeasurably longer time than even the 14∙10 9years lifetime of the universe.
3 Kinetic Theory of Vitrification
As already stated, vitrification on cooling is tantamount to bypassing crystallization, which would bring the material to an ordered state of matter of lower energy and, thus, of greater stability. If cooled quickly enough, virtually any material can vitrify. Hence, an important question is to know how fast the melt should be cooled to avoid detectable crystallization. Actually, the cooling rates of good glass formers range from 1 to 10 K/s and those of poor ones are higher than ~100 K/s. Familiar glass‐forming materials such as SiO 2‐rich silicates thus do not require fast cooling. An extreme example is supercooled NaAlSi 3O 8, which did not crystallize at all after five years spent 90 K below the melting point of the albite feldspar mineral [4]. Even though the quenching rate of a liquid medium can be increased to about 10 3K/s, such high values may not be fast enough to avoid partial or complete crystallization. In silicates, SiO 2‐poor olivine compositions (e.g. Mg 2SiO 4) are notorious examples of liquids that are difficult to vitrify at such rates [5]. Quickly crystallizing liquids such as metals may require still faster cooling. For instance, early metallic glasses ( Chapter 7.10) had to be splat quenched in the form of thin ribbons at about 10 6K/s to avoid crystallization, mainly because their viscosities remain very low with decreasing temperatures ( Figure 1).
An added complication is that melts can be good glass formers only within limited composition regions as indicated in Figure 2for aluminosilicates. Compilations of glass‐forming regions of phase diagrams are available [6–8]. As a rule, however, glass formation is enhanced in more complex systems. Oxide systems containing a variety of cations are easier to obtain in a glassy state as their liquidus temperature is lower and their complexity necessitates longer times for diffusion‐controlled redistribution of their diverse constituents before crystal nucleation and growth can take place.
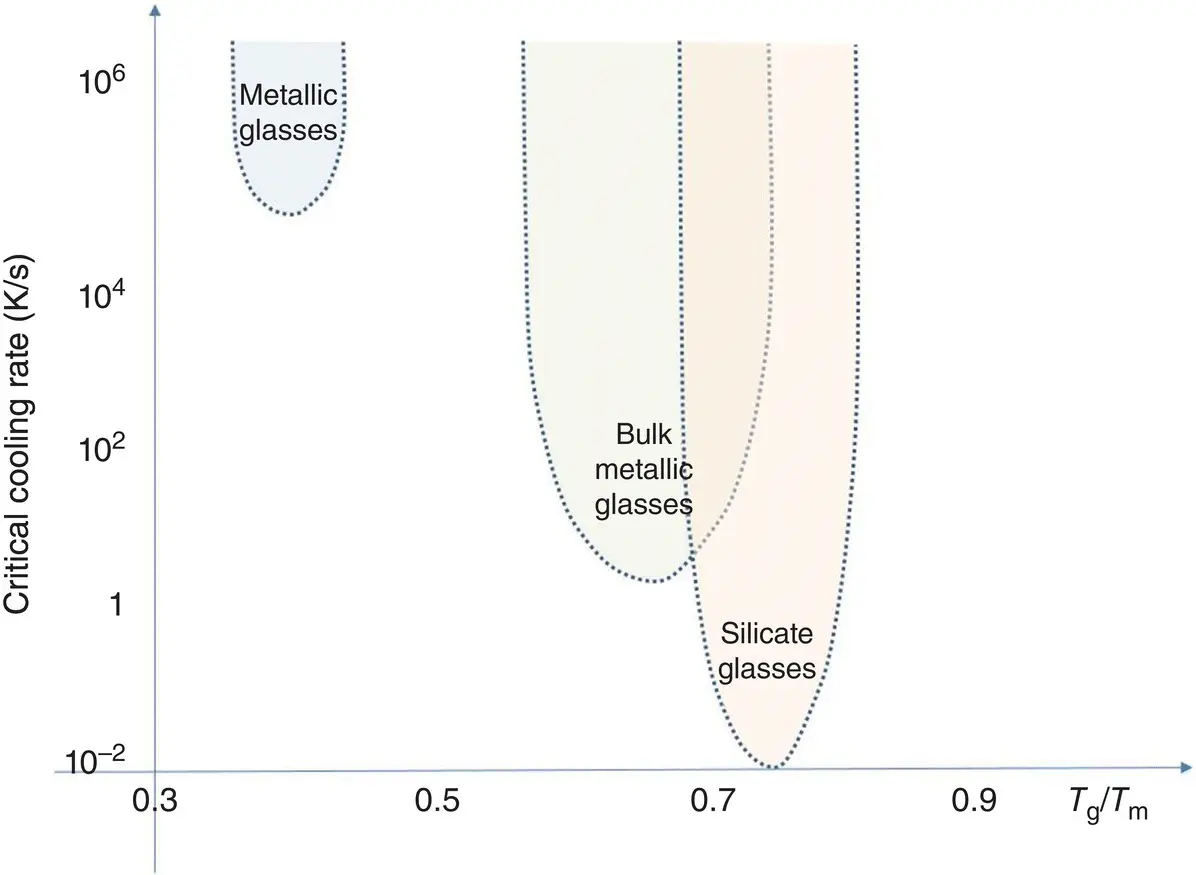
Figure 1 Critical cooling rates for glass formation. Reduced glass transition temperature T rgdefined as T g/ T m, where T mis the liquidus temperature.
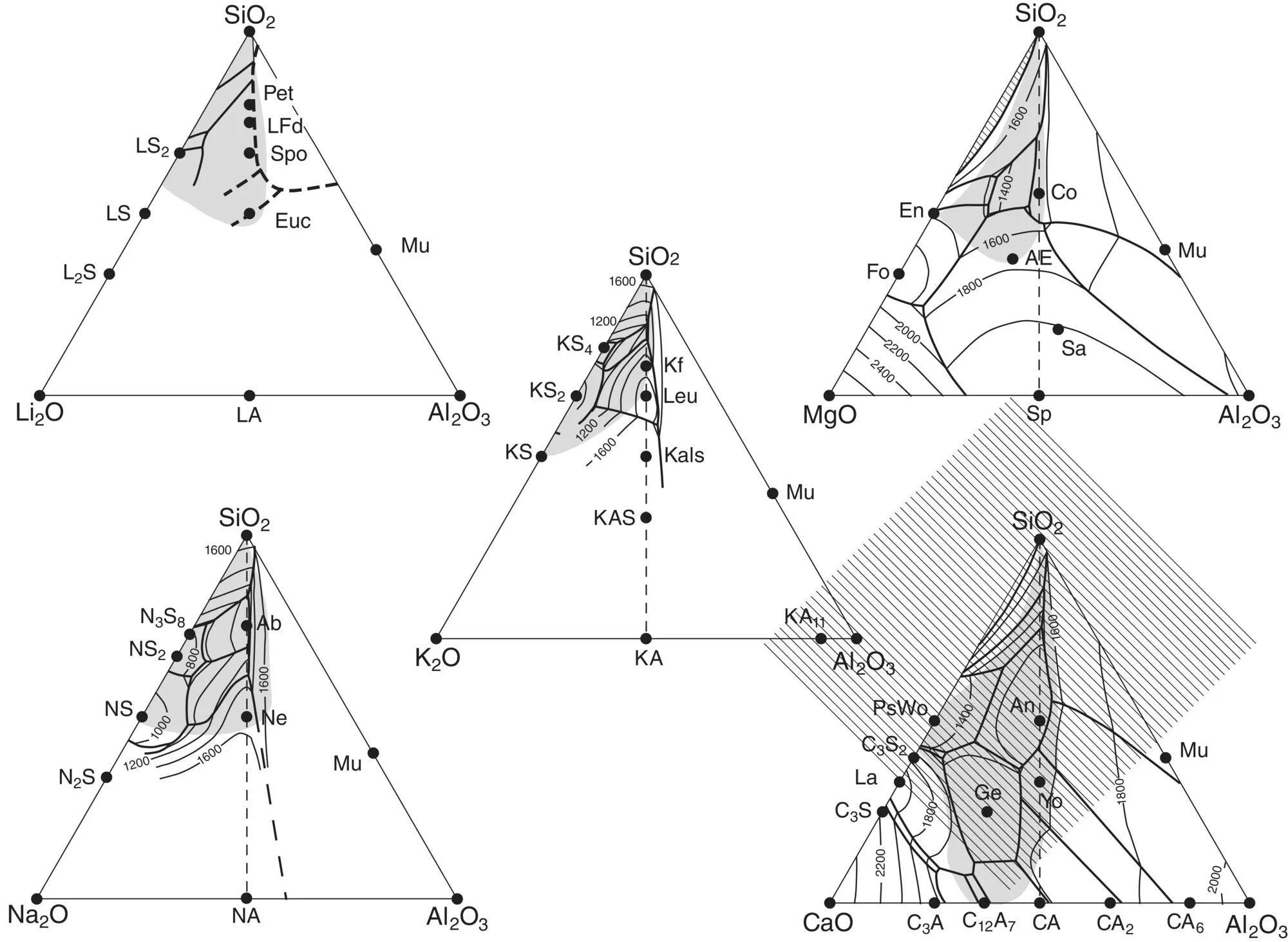
Figure 2 Glass formation ranges in aluminosilicate systems (shaded areas).
Source: After [6], courtesy P. Richet.
If crystallization is bypassed, the melt undergoes the glass transition in a temperature range that shifts to higher temperatures for higher cooling rates. Both the width of this range and the value of T gwithin it may vary by typically several tens of degrees. As the width and variation are small compared with T g, it is therefore possible to manage a cooling schedule rapid enough to keep the degree of crystallization negligible. Volume fractions considered to be negligible are lower than 1 ppm, which is the typical instrumental limit for detecting the presence of crystals by microanalytical techniques ( Chapter 2.3).
If v designates the volume fraction of crystalline(s) phase(s), the material is amorphous if v = 0, crystalline if v = 1, and polyphase or heterogeneous when 0 < v < 1. Under isothermal conditions the volume fraction of a growing crystalline phase varies with time as described by the Johnson–Mehl–Avrami–Kolmogorov equation (see [9] for references and details):
(1) 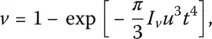
where u is the rate of crystal growth and I vthe nucleation rate.
If both rates can be estimated, the volume fraction of the crystalline phase v achieved for a given cooling rate can be calculated and the results be compared with experimental data. The rate of homogeneous nucleation is given by James equation:
(2) 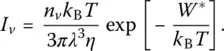
Here W * is the thermodynamic barrier to homogeneous nucleation, n vthe number of molecules or formula units of nucleating phase per unit volume, λ a jump distance, and η viscosity. For heterogeneous nucleation, the thermodynamic barrier to nucleation actually becomes W h* = W *(2 + cos θ )(1 − cos θ ) 2/4, where θ is the contact angle between the crystal and the nucleating heterogeneity. The rate of crystal growth is given by Wilson–Frenkel equation:
(3) 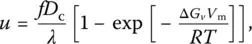
Читать дальше