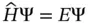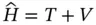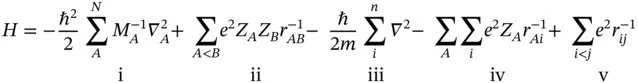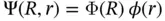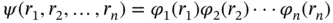Yu Lan - Computational Methods in Organometallic Catalysis

82 82 Miyaura, N., Yamada, K., and Suzuki, A. (1979). A new stereospecific cross‐coupling by the palladium‐catalyzed reaction of 1‐alkenylboranes with 1‐alkenyl or 1‐alkynyl halides. Tetrahedron Letters 20 (36): 3437–3440.

83 83 King, A.O., Okukado, N., and Negishi, E.‐i. (1977). Highly general stereo‐, regio‐, and chemo‐selective synthesis of terminal and internal conjugated enynes by the Pd‐catalysed reaction of alkynylzinc reagents with alkenyl halides. Journal of the Chemical Society, Chemical Communications 19: 683.

84 84 Milstein, D. and Stille, J.K. (1978). A general, selective, and facile method for ketone synthesis from acid chlorides and organotin compounds catalyzed by palladium. Journal of the American Chemical Society 100: 3636–3638.

85 85 Sonogashira, K., Tohda, Y., and Hagihara, N. (1975). A convenient synthesis of acetylenes: catalytic substitutions of acetylenic hydrogen with bromoalkenes, iodoarenes and bromopyridines. Tetrahedron Letters 16 (50): 4467–4470.

86 86 Vineyard, B.D., Knowles, W.S., Sabacky, M.J. et al. (1977). Asymmetric hydrogenation. Rhodium chiral bisphosphine catalyst. Journal of the American Chemical Society 99 (18): 5946–5952.

87 87 Qi, X., Liu, S., and Lan, Y. (2016). Computational studies on an aminomethylation precursor: (Xantphos)Pd(CH2NBn2)+. Organometallics 35: 1582–1585.

88 88 Li, Y., Liu, S., Qi, Z. et al. (2015). The mechanism of N—O bond cleavage in rhodium‐catalyzed C—H bond functionalization of quinoline N‐oxides with alkynes: a computational study. Chemistry – A European Journal 21: 10131–10137.

The core requirement of quantum chemistry is the solution of the time‐independent Schrödinger equation

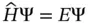
where Ĥ is the Hamiltonian operator, Ψ is the wavefunction for all of the nuclei and electrons, and E is the energy associated with this wavefunction. The Hamiltonian contains all operators that describe the kinetic and potential energy of the molecule at hand. Schrödinger equation is the basis of quantum mechanics, which was proposed by E. Schrödinger, an Austrian theoretical physicist, in 1926 [1–3]. It describes the law of the state of microparticles changing with time. The state of microsystem can be described by wavefunctions, whose differential equation is Schrödinger equation. It means that the wavefunctions can be solved by the equation, when the initial conditions and boundary conditions are given.

The Hamiltonian operator Ĥ can be broken into two operators

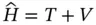
Those two operators represent kinetic energy ( T ) and potential energy ( V ), respectively. It could be further broken according to the nuclei and electron parts as

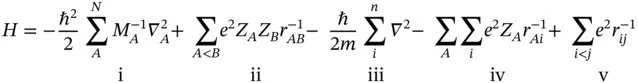
which represent (i) kinetic energy of nuclei, (ii) nuclear–nuclear repulsions, (iii) kinetic energy of electrons, (iv) nuclear–electron attraction, and (v) electron–electron repulsion. In most cases, it is impossible and unnecessary to find an analytic solution for the existing Schrödinger equation.

For organic system, several assumptions are indispensable to arrive at a solution due to the excessive degree of freedom. One of the most important assumptions is the Born Oppenheimer approximation proposed by M. Born and R. Oppenheimer in 1927 [4]. Considering that the nucleus is much larger than the electron generally by 3–4 orders, the moving of the electron should be much more rapid than that of the nucleus under the same interaction. The result of this difference in velocity is that the electron moves at every moment as if it were in a potential field composed of stationary nucleus, while the nucleus cannot observe the specific position of electrons and can only be averaged interactions. Thus, the variables of nuclear coordinates and electronic coordinates can be approximately separated. The complex process of solving the whole‐wave function can be decomposed into two relatively simple processes, solving the electronic wavefunction and solving the nuclear wavefunction

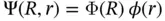
This separation of the total wavefunction into an electronic wavefunction ϕ ( r ) and a nuclear wavefunction Ф( R ) means that the positions of the nuclei can be fixed and then one only has to solve the Schrödinger equation for the electronic part. Usually, we only focus on the electron energy of the potential energy surface, which is determined by the electronic wavefunction ϕ ( r ). Therefore, the Hamiltonian obtained after applying the Born–Oppenheimer approximation and neglecting relativity is

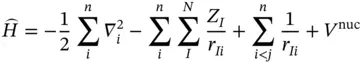
where V nucis the nuclear–nuclear repulsion energy.

In 1930, Hartree–Fock (HF) theory was formulated by V. Fock and D. R. Hartree, which is the basis of any other methods for solving Schrödinger equation [5, 6]. The core of HF theory is to simplify the problem of solving the multiparticle system in the external field into a problem of solving the wavefunction of a single particle. The electronic wavefunction can be separated into a product of functions that depend only on one electron

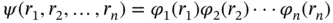
Unfortunately, the effect of electron–electron repulsion cannot be solved; therefore, the Schrödinger equation still cannot be solved exactly. Alternatively, the exact electron–electron repulsion is replaced with an effective field V i effproduced by the average positions of the remaining electrons. With this assumption, the separable functions ϕ isatisfy the Hartree equations

In the above‐mentioned equation, solving for a set of functions ϕ iis still problematic because the effective field V i effis dependent on the wavefunctions. To solve this problem, an iterative procedure, named self‐consisted field (SCF), was proposed by D. R. Hartree in 1927. First, a set of functions ( ϕ 1, ϕ 2, …, ϕ n) is assumed, which can be used to produce the set of effective potential operators V i effand the Hartree equations are solved to produce a set of improved functions ϕ i. These new functions produce an updated effective potential, which, in turn, yields a new set of functions ϕ i. This procedure is repeated until the functions ϕ ino longer change (converge) and produce an SCF. SCF convergence is a necessity for energy calculations.