Yu Lan - Computational Methods in Organometallic Catalysis

To further simplify approximation of wavefunctions, linear combination of atomic orbitals (LCAO) theory was proposed by Roothaan in 1951 [7, 8]. A LCAO is a quantum superposition of atomic orbitals and a technique for calculating molecular orbitals in quantum chemistry. In a mathematical sense, these wavefunctions are the basis set of functions, the basis functions, which describe the electrons of a given atom. In chemical reactions, orbital wavefunctions are modified, i.e. the electron cloud shape is changed, according to the type of atoms participating in the chemical bond.

An initial assumption is that the number of molecular orbitals is equal to the number of atomic orbitals included in the linear expansion. In a sense, n atomic orbitals combine to form n molecular orbitals, which can be numbered i = 1 to n and which may not all be the same. The linear expansion for the i th molecular orbital would be

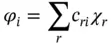
where φ iis a molecular orbital represented as the sum of n atomic orbitals χ r, each multiplied by a corresponding coefficient c ri, and r (numbered 1 to n ) represents which atomic orbital is combined in the term. The coefficients are the weights of the contributions of the n atomic orbitals to the molecular orbital. The Hartree–Fock procedure is used to obtain the coefficients of the expansion. The orbitals are thus expressed as linear combinations of basis functions, and the basis functions are one‐electron functions, which may or may not be centered on the nuclei of the component atoms of the molecule. In either case, the basis functions are usually also referred to as atomic orbitals, which are typically those of hydrogen‐like atoms since these are known analytically, i.e. Slater‐type orbitals (STOs), but other choices are possible such as the Gaussian‐type functions from standard basis sets or the pseudo‐atomic orbitals from plane‐wave pseudopotentials.

Because HF theory uses an effective electron–electron repulsion term, HF energy, E HF, will always be greater than the exact energy E . The instantaneous electron–electron repulsion is referred to as electron correlation, which is the best‐case error of HF theory.

This equation ignores relativistic effects, which are very small for typical organometallic molecules; however, it can be significant for heavier elements. In computational chemistry, post‐HF methods are the set of methods developed to improve on the HF method. They add electron correlation, which is a more accurate way of including the repulsions between electrons than in the HF method where repulsions are only averaged.

Methods that use more than one determinant are not strictly post‐HF methods, as they use a single determinant as reference, but they often use similar perturbation, or configuration interaction (CI) methods to improve the description of electron correlation. The usually used post‐HF methods include configuration interaction (CI) [9], coupled cluster (CC) [10], Møller–Plesset (MP) perturbation theory (MP2, MP3, MP4, etc.) [11–15], quadratic configuration interaction (QCI) [16], and quantum chemistry composite methods [G2, G3, complete basis set (CBS), W1, etc.] [17–22].

CI is a post‐HF linear variational method for solving the nonrelativistic Schrödinger equation within the Born–Oppenheimer approximation for a quantum chemical multielectron system. Mathematically, configuration simply describes the linear combination of Slater determinants or configuration state functions (CSFs) used for the wavefunction. In terms of a specification of orbital occupation, interaction means the mixing (interaction) of different electronic configurations (states). Due to the long CPU time and large memory required for full CI calculations, the method is limited to relatively small systems. Truncating the CI space is important to save computational time. For example, the method configuration interaction with doubles (CID) is limited to double excitations only [13]. The method configuration interaction with singles and doubles (CISD) is limited to single and double excitations. Single excitations on their own do not mix with the HF determinant [23]. The Davidson correction can be used to estimate a correction to the CISD energy to account for higher excitations. It was used to solve the important problem of truncated CI methods is their size inconsistency, which means the energy of two infinitely separated particles is not double that of the single particle.

QCI is an extension of CI that corrects for size‐consistency errors in single‐ and double‐excitation CI methods (CISD). Size consistency means that the energy of two noninteracting (i.e. at large distance apart) molecules calculated directly will be the sum of the energies of the two molecules calculated separately. This method called quadratic configuration interaction with singles and doubles (QCISD) was developed in the group of J. Pople in 1989 [24, 25]. It gives results that are comparable to the CC method, coupled cluster single double (CCSD) [26, 27]. QCISD can be improved by the same perturbative inclusion of unlinked triples to give QCISD(T) [16]. This gives similar results to CCSD(T) [28].

CC is a numerical technique used for describing many‐body systems. CC essentially takes the basic HF molecular orbital method and constructs multielectron wavefunctions using the exponential cluster operator to account for electron correlation. Some of the most accurate calculations for small‐to‐medium‐sized molecules use this method. The choice of the exponential ansatz is opportune because it guarantees the size extensive of the solution. Size consistency in CC theory, unlike other theories, does not depend on that of the reference wavefunction. This is easily seen, for example, in the single‐bond breaking of F 2when using a restricted HF reference, which is not size consistent, at the coupled‐cluster single double triple (CCSDT) [29, 30] level of theory, which provides an almost exact, full CI quality, potential energy surface and does not dissociate the molecule into F −and F +ions, like the restricted Hartree−Fock (RHF) wavefunction, but rather into two neutral F atoms. If one were to use, for example, the CCSD, or CCSD(T) levels of theory, they would not provide reasonable results for the bond breaking of F 2, with the latter one approaches unphysical potential energy surfaces, though this is for reasons other than just size consistency.

MP perturbation theory improves on the HF method by adding electron correlation effects by means of Rayleigh–Schrödinger perturbation theory (RS‐PT) [31], usually to second (MP2), third (MP3), or fourth (MP4) order. Its main idea was published as early as 1934 by Møller and Plesset [11].

Quantum chemistry composite methods are computational chemistry methods that aim for high accuracy by combining the results of several calculations. They combine methods with a high level of theory and a small basis set with methods that employ lower levels of theory with larger basis sets. They are commonly used to calculate thermodynamic quantities such as enthalpies of formation, atomization energies, ionization energies, and electron affinities. They aim for chemical accuracy, which is usually defined as within 1 kcal/mol of the experimental value.

The first systematic model chemistry of this type with broad applicability was called Gaussian‐1 (G1) introduced by Pople et al. [32]. This was quickly replaced by the Gaussian‐2 (G2), which has been used extensively [33]. The Gaussian‐3 (G3) was introduced later [17]. The current version of this series of methods is Gaussian‐4 (G4) [34]. G4 theory is an improved modification of the earlier approach G3 theory.