Yu Lan - Computational Methods in Organometallic Catalysis

The CBS methods are a family of composite methods, the members of which are: CBS‐4M, CBS‐QB3, and CBS‐APNO, in increasing order of accuracy [35]. The CBS methods were developed by G. Petersson and coworkers, and they extrapolate several single‐point energies to the “exact” energy. In comparison, the Gaussian‐ n methods perform their approximation using additive corrections. Similar to the modified G2(+) method, CBS‐QB3 has been modified by the inclusion of diffuse functions in the geometry optimization step to give CBS‐QB3(+).

As a summary, although the above‐mentioned post‐HF methods could be often obtained with higher accuracy than HF method, they are still unable to be directly applied to the mechanistic study of transition metal catalysis because of the rather expensive time consumption. In fact, those methods are often used as a reference of energy to test the accuracy of some other more efficient computational methods.

The inefficiency of HF and post‐HF methods is the high computational effort that is required for the treatment of relatively large molecular systems. Therefore, it is rather complicated to solve. Fortunately, the total electron density of a molecule is only dependent on three variables in space, which is simpler than the electronic wavefunction and is also observable. It would offer a more direct way to obtain the molecular properties by the calculation of electron density.

The Hohenberg–Kohn existence theorem proves just that the ground state of any interacting many particle system with a given fixed inter-particle interaction is a unique functional of the electron density [36]. There exists a unique functional such that

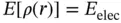
where E elecis the exact electronic energy. It could be considered to be a functional, in which the function ρ ( r ) depends on the spatial coordinates, and the energy depends on the values (is a functional) of ρ ( r ).

To solve for the energy via the density functional theory (DFT) method, Kohn and Sham proposed that the functional has the form

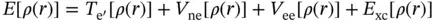
where T e′is the kinetic energy of noninteracting electrons whose density is the same as the density of the real electrons, the true interacting electrons. V neis the nuclear–electron attraction term. V eeis the classical electron–electron repulsion [37]. The last term is called the exchange–correlation functional, and is a catch‐all term to account for all other aspects of the true system. However, it offers no guidance as to the form of that functional.

The exchange–correlation functional is generally written as a sum of two components, an exchange part and a correlation part. This is an assumption, an assumption that we have no way of knowing is true or not. These component functionals are usually written in terms of an energy density ε

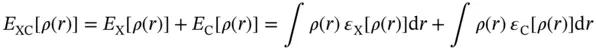
The major problem with DFT is that the exact functionals for exchange and correlation are not known except for the free electron gas. However, approximations exist, which permit the calculation of certain physical quantities quite accurately. One of the initial simple approximations of exchange–correlation functional is the local‐density approximation (LDA), in which the exchange–correlation functional of uniform electron gas with same density is used as the approximation of the corresponding nonuniform system [38]. Unexpectedly, such a simple approximation often yields good results, which directly led to the widespread application of DFT currently. If the electron densities of different spin components are further considered, the local spin density approximation (LSDA) can be obtained. Despite the great success of L(S)DA, there are many shortcomings, such as systematic overestimation of binding energies.

To make improvements over the L(S)DA, one has to assume that the density is not uniform. The approach that has been taken is to develop functionals that are dependent on not just the electron density but also derivatives of the density. This constitutes the generalized gradient approximation (GGA). It is at this point that the form of the functionals begins to cause the eyes to glaze over and the acronyms to appear to be random samplings from an alphabet soup. The method of constructing GGA exchange–correlation functional can be divided into two ways. One is the group headed by Becke, which believes that “everything is allowed.” Any formation of exchange–correlation functionals for any reason can be chosen, while the quality of this formation only depends on the comparison with real system. Another group, led by Perdew, believes that the development of exchange–correlation functionals should be based on certain physical laws, such as scaling relations and progressive behavior.

Indeed, there is no unified standard for the classification of density functionals in the physical chemistry field. In 2001, J. P. Perdew et al. proposed using “Jacob's ladder” to classify the level of density functionals [39, 40]. As shown in Scheme 2.1, the ground in the “Jacob's ladder” is HF theory, which is an imprecise method with neither exchange energy nor correlation energy. In fact, HF calculation is rarely used in theoretical and computational chemistry nowadays.

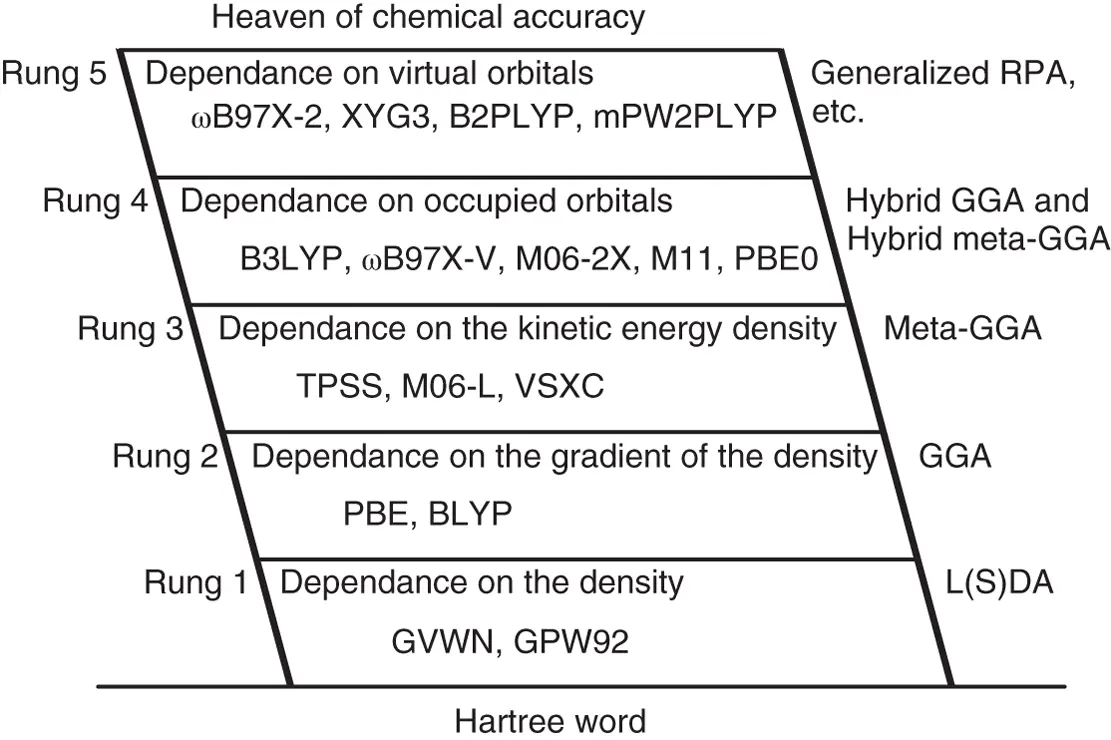
Scheme 2.1 Jacob's ladder of density functionals.

The first rung in “Jacob's ladder” is the density functional based on L(S)DA, the variable in which kind of functionals is the local spin density. The exchange functional of L(S)DA can be written as analytic expressions, which is often called Slater or Dirac exchange functional. However, the correlation functional of L(S)DA has no analytic expression, and can only be fitted by a functional with parameters from the results of high‐level calculations on some uniform electron gases. L(S)DA has achieved surprising success in the early works on the computational study of solid‐state physics. However, it is failure in computational chemistry because L(S)DA usually overestimates the bonding energy.

The second rung in “Jacob's ladder” of density functionals is the GGA. The variables in this kind of functionals are local spin density and its gradient. Therefore, there are no analytic expressions for both exchange functionals and correlation functionals of GGA density functionals. The first successful GGA density functional for chemical calculation was Becke–Lee–Yang–Parr hybrid DFT functional (BLYP) [41, 42]. Thereinto, B was Becke88 exchange functional, while LYP was Lee–Yang–Parr correlation functional. Around 2000, the commonly used GGA functionals in computational organometallic chemistry are the Perdew–Burke–Ernzerh (PBE) and BP86 functionals [43, 44]. Although these functionals are seldom used at present, many of popular functionals are developed on the basis of these functionals.