1 ...6 7 8 10 11 12 ...16 [1.12] 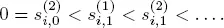
Then 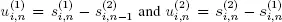 denote the length of the n th blocked and the n th available period for the i th server, respectively,
denote the length of the n th blocked and the n th available period for the i th server, respectively, 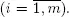 The sequence
The sequence 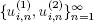 consists of iid random vectors (for all
consists of iid random vectors (for all 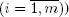 ) and these sequences do not depend on the input flow X and service times. Let
) and these sequences do not depend on the input flow X and service times. Let 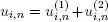 be the length of the n th cycle for the server i . A cycle consists of a blocked period followed by an available period. We assume that
be the length of the n th cycle for the server i . A cycle consists of a blocked period followed by an available period. We assume that
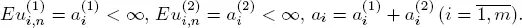
We put ni ( t ) = 0 if the i th server is in an unavailable state at time t and ni(t) = 1, otherwise 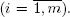 If a blocked period
If a blocked period 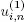 has an exponential phase, i.e.
has an exponential phase, i.e. 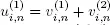 where
where 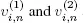 are independent random variables and
are independent random variables and 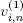 has an exponential distribution with a parameter αi , then we may define the sequence
has an exponential distribution with a parameter αi , then we may define the sequence 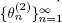 of regeneration points for the regenerative process
of regeneration points for the regenerative process 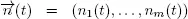 as above. Therefore, condition 1.6 holds. Under condition 1.7, the auxiliary process Y is strongly regenerative and we can construct the common points of regeneration
as above. Therefore, condition 1.6 holds. Under condition 1.7, the auxiliary process Y is strongly regenerative and we can construct the common points of regeneration 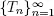 for X and Y and apply theorems 1.1 and 1.2 for this model. Since
for X and Y and apply theorems 1.1 and 1.2 for this model. Since
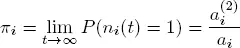
we have from [1.11]
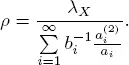
If bi = b , then we get the same stability condition as obtained in Morozov et al . (2011) for a queueing system GI|G|m with a common distribution function of service times for all servers.
COROLLARY 1.1.– For a queueing system with 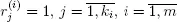
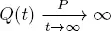
if ρ > I.
Under condition 1.4, the process is stochastically bounded if ρ < 1.
PROOF.– Let, as before, 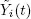 be the number of customers actually served on the i th server up to time t . It is evident that stochastic inequality
be the number of customers actually served on the i th server up to time t . It is evident that stochastic inequality
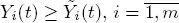
for t > 0 takes place and hence
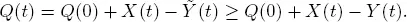
Since 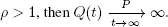
To prove the second statement, we first assume that conditions 1.6 and 1.7 hold. Then condition 1.1 for the process Y takes place. We also may organize the performance of the systems S and S 0in such a way that inequality [1.8]is realized when 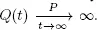 Thus, conditions 1.1, 1.4 and 1.5 are satisfied and because of theorem 1.2 the process Q is stochastically bounded.
Thus, conditions 1.1, 1.4 and 1.5 are satisfied and because of theorem 1.2 the process Q is stochastically bounded.
If conditions 1.6 and 1.7 (or one of them) are not valid, we construct a system Sδ satisfying conditions 1.6 and 1.7 and majorising our system S , so that in distribution
[1.13] 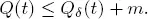
Here, Qδ ( t ) is the number of customers in the system Sδ at instant t . Let us introduce independent sequences 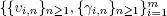 of iid random variables with exponential distribution with a rate δ . Assume that repair time
of iid random variables with exponential distribution with a rate δ . Assume that repair time 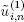 in the system Sδ has the form
in the system Sδ has the form 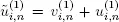 and service time
and service time 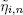 by the i th server has the form
by the i th server has the form 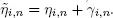
Then Sδ satisfies conditions 1.6 and 1.7. Since 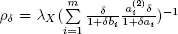 and
and 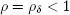 we may choose δ so that ρδ < 1.
we may choose δ so that ρδ < 1.
Читать дальше

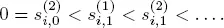
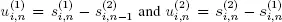 denote the length of the n th blocked and the n th available period for the i th server, respectively,
denote the length of the n th blocked and the n th available period for the i th server, respectively, 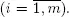 The sequence
The sequence 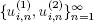 consists of iid random vectors (for all
consists of iid random vectors (for all 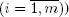 ) and these sequences do not depend on the input flow X and service times. Let
) and these sequences do not depend on the input flow X and service times. Let 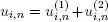 be the length of the n th cycle for the server i . A cycle consists of a blocked period followed by an available period. We assume that
be the length of the n th cycle for the server i . A cycle consists of a blocked period followed by an available period. We assume that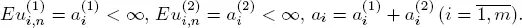
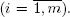 If a blocked period
If a blocked period 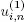 has an exponential phase, i.e.
has an exponential phase, i.e. 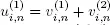 where
where 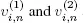 are independent random variables and
are independent random variables and 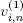 has an exponential distribution with a parameter αi , then we may define the sequence
has an exponential distribution with a parameter αi , then we may define the sequence 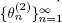 of regeneration points for the regenerative process
of regeneration points for the regenerative process 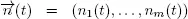 as above. Therefore, condition 1.6 holds. Under condition 1.7, the auxiliary process Y is strongly regenerative and we can construct the common points of regeneration
as above. Therefore, condition 1.6 holds. Under condition 1.7, the auxiliary process Y is strongly regenerative and we can construct the common points of regeneration 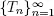 for X and Y and apply theorems 1.1 and 1.2 for this model. Since
for X and Y and apply theorems 1.1 and 1.2 for this model. Since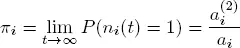
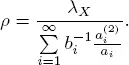
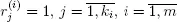
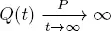
 be the number of customers actually served on the i th server up to time t . It is evident that stochastic inequality
be the number of customers actually served on the i th server up to time t . It is evident that stochastic inequality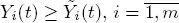
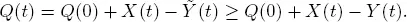
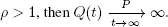
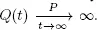 Thus, conditions 1.1, 1.4 and 1.5 are satisfied and because of theorem 1.2 the process Q is stochastically bounded.
Thus, conditions 1.1, 1.4 and 1.5 are satisfied and because of theorem 1.2 the process Q is stochastically bounded.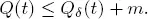
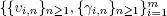 of iid random variables with exponential distribution with a rate δ . Assume that repair time
of iid random variables with exponential distribution with a rate δ . Assume that repair time 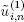 in the system Sδ has the form
in the system Sδ has the form 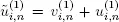 and service time
and service time 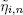 by the i th server has the form
by the i th server has the form 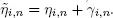
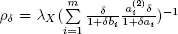 and
and 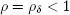 we may choose δ so that ρδ < 1.
we may choose δ so that ρδ < 1.










