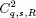1 Cover
2 Title Page SCIENCES Mathematics , Field Director – Nikolaos Limnios Queuing Theory and Applications , Subject Head – Vladimir Anisimov
3 Copyright First published 2020 in Great Britain and the United States by ISTE Ltd and John Wiley & Sons, Inc. Apart from any fair dealing for the purposes of research or private study, or criticism or review, as permitted under the Copyright, Designs and Patents Act 1988, this publication may only be reproduced, stored or transmitted, in any form or by any means, with the prior permission in writing of the publishers, or in the case of reprographic reproduction in accordance with the terms and licenses issued by the CLA. Enquiries concerning reproduction outside these terms should be sent to the publishers at the undermentioned address: ISTE Ltd 27-37 St George’s Road London SW19 4EU UK www.iste.co.uk John Wiley & Sons, Inc. 111 River Street Hoboken, NJ 07030 USA www.wiley.com © ISTE Ltd 2020 The rights of Vladimir Anisimov and Nikolaos Limnios to be identified as the author of this work have been asserted by them in accordance with the Copyright, Designs and Patents Act 1988. Library of Congress Control Number: 2019957522 British Library Cataloguing-in-Publication Data A CIP record for this book is available from the British Library ISBN 978-1-78945-004-0 ERC code: PE1 Mathematics PE1_21 Application of mathematics in industry and society
4 Preface
5 1 Stability Analysis of Queueing Systems based on Synchronization of the Input and Majorizing Output Flows
1.1. Introduction 1.2. Model description 1.3. Auxiliary service process 1.4. Instability result for the case ρ ≥ 1 1.5. Stochastic boundedness for the case ρ < 1 1.6. Queueing system with unreliable servers and preemptive resume service discipline 1.7. Discrete-time queueing system with interruptions and preemptive repeat different service discipline 1.8. Queueing system with a preemptive priority discipline 1.9. Queueing system with simultaneous service of a customer by a random number of servers 1.10. Applications to transport systems analysis 1.11. Conclusion 1.12. Acknowledgment 1.13. References
6 2 Queueing Models in Services – Analytical and Simulation Approach 2.1. Introduction 2.2. Phase-type distributions and the batch Markovian arrival process 2.3. Generation of MAP processes for numerical purposes 2.4. Analysis of selected queueing models of BMAP/G/c type 2.5. Simulated models of BM AP/G/c type queues 2.6. Analysis of selected queueing models of BMAP/G/c type with a vacation 2.7. Acknowledgment 2.8. References
7 3 Distributions and Random Processes Related to Queueing and Reliability Models 3.1. Some useful notations, relationships and interpretations 3.2. Unreliable service model and reliability maintenance 3.3. Characterizations of exponential and geometric distributions via properties of service times 3.4 Probability distributions almost having lack of memory property 3.5. Random processes with a periodic nature 3.6. Conclusions 3.7. References
8 4 The Impact of Information Structure on Strategic Behavior in Queueing Systems 4.1. Introduction 4.2. Game-theoretical framework in queueing 4.3. The unobservable model 4.4. The observable model 4.5. Comparison of the unobservable and the observable models 4.6. Partially observable models 4.7. Heterogeneously observable models 4.8. Observable-with-delay models 4.9. Conclusions and literature review for further study 4.10. Acknowledgments 4.11. References
9 5 Non-extensive Maximum Entropy Formalisms and Inductive Inference of a Stable M/G/1 Queue with Heavy Tails 5.1 Introduction 5.2 General systems and inductive ME formalisms 5.3. NME formalisms and EME consistency axioms 5.4. A stable M/G/1 queue with long-range interactions 5.5. Numerical experiments and interpretations 5.6. Conclusions 5.7. Acknowledgments 5.8. Appendix: Rényi’s NME formalisms versus EME consistency axioms 5.9. References
10 6 Inventory with Positive Service Time: a Survey 6.1. Introduction 6.2. Queueing inventory models 6.3. Acknowledgment 6.4. References
11 7 A Stability Analysis Method of Regenerative Queueing Systems 7.1. Introduction 7.2. Preliminaries 7.3. The single-server system 7.4. The zero-delayed multiserver system 7.5. The delayed multiserver system: finiteness of the first regeneration period 7.6. Instability 7.7. Related research 7.8. Acknowledgments 7.9. References
12 8 Transient Analysis of Markovian Queueing Systems: a Survey with Focus on Closed-forms and Uniformization 8.1. Introduction 8.2. Basics on Markovian queues 8.3. First examples 8.4. An uniformization-based path for the M / M /1 with matrix generating functions 8.5. An uniformization-based path using duality 8.6. Other transient results 8.7. Conclusion 8.8. References
13 List of Authors
14 Index
15 End User License Agreement
1 Chapter 1 Figure 1.1. A road intersected by a pedestrian crossing Figure 1.2. Plots for α = 0.5, 1.5, 2
2 Chapter 2 Figure 2.1. One-lag correlation coefficient of MAPs under different scenarios. F... Figure 2.2. Selected measures for a MAP/PH/1 queue under different scenarios Figure 2.3. Tail probabilities for the sojourn time for a MAP/PH/ 1 queue under d... Figure 2.4. The distribution function of the sojourn time for a MAP/PH/1 queue u... Figure 2.5. Selected measures for a MAP/M/c queue under different scenarios Figure 2.6. Ratio of the mean busy period to the mean sojourn time for (simulate...Figure 2.7. Ratio of the mean queue length for MAP/PH/ 1 vacation to MAP/PH/ 1 cla...Figure 2.8. Ratio of the system idle probability for vacation and classical MAP/...Figure 2.9. The distribution functions of the sojourn time for MAP/PH/ 1 classica...Figure 2.10. The distribution functions of the sojourn time for MAP/PH/ 1 classic...Figure 2.11. Selected measures for (simulated) a BMAP/PH/c queue with a vacation...Figure 2.12. The tail probabilities of the sojourn time for (simulated) a BMAP/G...
3 Chapter 5Figure 5.1. The GE-type distribution with parameters Figure 5.2.  versus n for
versus n for 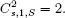 For a color version of this figure, see www.iste.co...Figure 5.3.
For a color version of this figure, see www.iste.co...Figure 5.3.  versus n for
versus n for 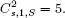 For a color version of this figure, see www.iste.co...Figure 5.4.
For a color version of this figure, see www.iste.co...Figure 5.4. 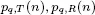 versus n for | For a color version of this figure, see www.iste.co...Figure 5.5.
versus n for | For a color version of this figure, see www.iste.co...Figure 5.5. 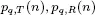 versus n for | For a color version of this figure, see www.iste.co...Figure 5.6.
versus n for | For a color version of this figure, see www.iste.co...Figure 5.6. 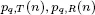 versus n for
versus n for 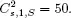 For a color version of this figure, see www.iste.co...Figure 5.7.
For a color version of this figure, see www.iste.co...Figure 5.7. 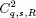
Читать дальше

 versus n for
versus n for 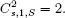 For a color version of this figure, see www.iste.co...Figure 5.3.
For a color version of this figure, see www.iste.co...Figure 5.3. 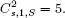 For a color version of this figure, see www.iste.co...Figure 5.4.
For a color version of this figure, see www.iste.co...Figure 5.4. 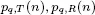 versus n for | For a color version of this figure, see www.iste.co...Figure 5.5.
versus n for | For a color version of this figure, see www.iste.co...Figure 5.5. 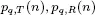 versus n for | For a color version of this figure, see www.iste.co...Figure 5.6.
versus n for | For a color version of this figure, see www.iste.co...Figure 5.6. 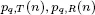 versus n for
versus n for 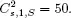 For a color version of this figure, see www.iste.co...Figure 5.7.
For a color version of this figure, see www.iste.co...Figure 5.7.