and

versus n for q for original | For a color version of this fi...Figure 5.8.

For a color version of this figure, see www.iste.co.uk/anisimov/q...Figure 5.9.
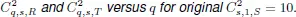
For a color version of this figure, see www.iste.co.uk/anisimov/q...Figure 5.10.
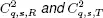 versus q for original
versus q for original 
For a color version of this figure, see w...Figure 5.11.

and
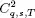 versus q for original
versus q for original 
For a color version of this figure,...
4 Chapter 8Figure 8.1. The evolution of an individual particle in the continuous-time Ehren...Figure 8.2. An example where a closed-form for the transient behavior is easy to...Figure 8.3. Uniformization of the M / M /1 canonical process w.r.t. the uniformizat...Figure 8.4. The Siegmund-dual of the standard birth-death process with birth rat...Figure 8.5. This is a pair ( X, X *) where the dual exists under specific conditio...Figure 8.6. Process X has no dual, whatever the value of λ (and, obviously, what...Figure 8.7. The dual Z * of the uniformization Z of the M / M /1 process, which is a...Figure 8.8. The M / M /1/ H model, parameters λ and μ Figure 8.9. The uniformized chain of the M / M /l/ H canonical process depicted in 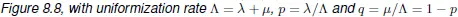 Figure 8.10. The dual process of the M / M /1/ H given in Figure 8.8 Figure 8.11. The dual of the uniformized chain shown in Figure 8.9, which is als...Figure 8.12. The smallest non-trivial irreducible Markov process with two states ...Figure 8.13. The M / M /1/ H model with catastrophes; parameters: arrival rate λ, se...Figure 8.14. The dual of the M / M /1/H model with catastrophes is depicted in Figu...Figure 8.15. The uniformization of the dual of the M / M /1/H model with catastroph...Figure 8.16. Auxiliary 2-dimensional process Y Figure 8.17. The uniformization of process Y depicted in Figure 8.16 with respec...Figure 8.18. A numerical example where λ = 0.95 and μ = 1 ; we plot
Figure 8.10. The dual process of the M / M /1/ H given in Figure 8.8 Figure 8.11. The dual of the uniformized chain shown in Figure 8.9, which is als...Figure 8.12. The smallest non-trivial irreducible Markov process with two states ...Figure 8.13. The M / M /1/ H model with catastrophes; parameters: arrival rate λ, se...Figure 8.14. The dual of the M / M /1/H model with catastrophes is depicted in Figu...Figure 8.15. The uniformization of the dual of the M / M /1/H model with catastroph...Figure 8.16. Auxiliary 2-dimensional process Y Figure 8.17. The uniformization of process Y depicted in Figure 8.16 with respec...Figure 8.18. A numerical example where λ = 0.95 and μ = 1 ; we plot 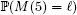 , for level ...
, for level ...
1 Chapter 2 Table 2.1. Selected MAPs Table 2.2. Error percentage for a MAP/M/c queue under selected scenarios Table 2.3. Error percentage for a MAP/PH/1 queue under selected scenarios Table 2.4. Best fit probability distribution for the sojourn time when c = 1, ρ ...Table 2.5. Best fit probability distribution for the sojourn time when c = 1, ρ ...Table 2.6. Error percentage for a MAP/PH/ 1 queue with a vacation under selected ...Table 2.7. Error percentage fora MAP/PH/ 1 queue with a vacation under selected s...Table 2.8. Best fit probability distribution for the sojourn time when c =1,ρ = ...
2 Chapter 6Table 6.1. An overview of studies on inventory models with positive service time
1 Cover
2 Table of Contents
3 Title Page SCIENCES Mathematics , Field Director – Nikolaos Limnios Queuing Theory and Applications , Subject Head – Vladimir Anisimov
4 Copyright First published 2020 in Great Britain and the United States by ISTE Ltd and John Wiley & Sons, Inc. Apart from any fair dealing for the purposes of research or private study, or criticism or review, as permitted under the Copyright, Designs and Patents Act 1988, this publication may only be reproduced, stored or transmitted, in any form or by any means, with the prior permission in writing of the publishers, or in the case of reprographic reproduction in accordance with the terms and licenses issued by the CLA. Enquiries concerning reproduction outside these terms should be sent to the publishers at the undermentioned address: ISTE Ltd 27-37 St George’s Road London SW19 4EU UK www.iste.co.uk John Wiley & Sons, Inc. 111 River Street Hoboken, NJ 07030 USA www.wiley.com © ISTE Ltd 2020 The rights of Vladimir Anisimov and Nikolaos Limnios to be identified as the author of this work have been asserted by them in accordance with the Copyright, Designs and Patents Act 1988. Library of Congress Control Number: 2019957522 British Library Cataloguing-in-Publication Data A CIP record for this book is available from the British Library ISBN 978-1-78945-004-0 ERC code: PE1 Mathematics PE1_21 Application of mathematics in industry and society
5 Preface
6 Begin Reading
7 List of Authors
8 Index
9 End User License Agreement
1 v
2 iii
3 iv
4 xi
5 xii
6 1
7 2
8 3
9 4
10 5
11 6
12 7
13 8
14 9
15 10
16 11
17 12
18 13
19 14
20 15
21 16
22 17
23 18
24 19
25 20
26 21
27 22
28 23
29 24
30 25
31 26
32 27
33 28
34 29
35 30
36 31
37 32
38 33
39 34
40 35
41 36
42 37
43 38
44 39
45 40
46 41
47 42
48 43
49 44
50 45
51 46
52 47
53 48
54 49
55 50
56 51
57 52
58 53
59 54
60 55
61 56
62 57
63 58
64 59
65 60
66 61
67 62
68 63
69 64
70 65
71 66
72 67
73 68
74 69
75 70
76 71
77 72
78 73
79 74
80 75
81 76
82 77
83 78
84 79
85 80
86 81
87 82
88 83
89 84
90 85
91 86
92 87
93 88
94 89
95 90
96 91
97 92
98 93
99 94
100 95
101 96
102 97
103 98
104 99
105 100
106 101
107 102
108 103
109 104
110 105
111 106
112 107
113 108
114 109
115 110
116 111
117 112
118 113
119 114
120 115
121 116
122 117
123 118
124 119
125 120
126 121
127 122
128 123
129 124
130 125
131 126
132 127
133 128
134 129
Читать дальше

 versus n for q for original | For a color version of this fi...Figure 5.8.
versus n for q for original | For a color version of this fi...Figure 5.8.  For a color version of this figure, see www.iste.co.uk/anisimov/q...Figure 5.9.
For a color version of this figure, see www.iste.co.uk/anisimov/q...Figure 5.9. 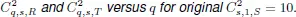 For a color version of this figure, see www.iste.co.uk/anisimov/q...Figure 5.10.
For a color version of this figure, see www.iste.co.uk/anisimov/q...Figure 5.10. 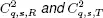 versus q for original
versus q for original  For a color version of this figure, see w...Figure 5.11.
For a color version of this figure, see w...Figure 5.11.  and
and 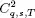 versus q for original
versus q for original  For a color version of this figure,...
For a color version of this figure,...
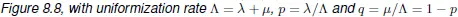 Figure 8.10. The dual process of the M / M /1/ H given in Figure 8.8 Figure 8.11. The dual of the uniformized chain shown in Figure 8.9, which is als...Figure 8.12. The smallest non-trivial irreducible Markov process with two states ...Figure 8.13. The M / M /1/ H model with catastrophes; parameters: arrival rate λ, se...Figure 8.14. The dual of the M / M /1/H model with catastrophes is depicted in Figu...Figure 8.15. The uniformization of the dual of the M / M /1/H model with catastroph...Figure 8.16. Auxiliary 2-dimensional process Y Figure 8.17. The uniformization of process Y depicted in Figure 8.16 with respec...Figure 8.18. A numerical example where λ = 0.95 and μ = 1 ; we plot
Figure 8.10. The dual process of the M / M /1/ H given in Figure 8.8 Figure 8.11. The dual of the uniformized chain shown in Figure 8.9, which is als...Figure 8.12. The smallest non-trivial irreducible Markov process with two states ...Figure 8.13. The M / M /1/ H model with catastrophes; parameters: arrival rate λ, se...Figure 8.14. The dual of the M / M /1/H model with catastrophes is depicted in Figu...Figure 8.15. The uniformization of the dual of the M / M /1/H model with catastroph...Figure 8.16. Auxiliary 2-dimensional process Y Figure 8.17. The uniformization of process Y depicted in Figure 8.16 with respec...Figure 8.18. A numerical example where λ = 0.95 and μ = 1 ; we plot 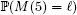 , for level ...
, for level ...










