We should consider that models with service interruptions occur in numerous applications including manufacturing processes, multiprocessor computer networks, telecommunicating networks and various types of service counters.
White and Christie (1958) were the first to study queueing systems with interruptions. Those authors investigated the M | M |1 model with preemptive resume priority discipline. Their results were later extended by (Avi-Itzhak and Naor 1963) and (Thiruvengadam 1963) who study queues with general service times. Gaver (1962) studied single-server queues with batch Poisson arrivals and generally distributed service times. So far there is extensive literature concerning queueing systems with interruptions. There are some review papers that cover most of the literature in this sphere. Some of the important papers on the single-server case are presented in Fiems and Bruneel (2013).
The most extensive literature survey on systems with interruptions both for single-server and multiserver cases is given by (Krishnamoorthy et al . 2012). This paper also covers some non-Markovian multichannel systems with homogeneous servers. There are some other articles with extensive literature survey as well (Pechinkin et al . 2009; Morozov et al . 2011). Nevertheless, to the best of our knowledge, there are no papers that study the stability problem for multichannel queueing systems with heterogeneous servers in non-Markovian case with general input flow and service times. Synchronization method combined with the regenerative theory is one of the powerful approaches to obtain stability conditions for such systems.
Let us also mention the fluid approximation approach as an alternative to the synchronization approach followed here. Such an approach has lent to significant progress in stability analysis of multiclass queueing networks (Dai 1995; Chen 1995; Chen and Yao 2001). See also Foss and Konstantopoulos (2004) for a survey of various approaches to stability of queueing systems with a focus on the fluid approach. Nevertheless, our analysis does not rely on a fluid approach because to the best of our knowledge, the synchronization method with regard to regenerative structure of the processes turns out to be suitable for obtaining complete and transparent proofs as well as natural stability conditions for the model at hand.
We also note that stability analysis is an essential and challenging stage of investigation of a stochastic model, however, stability conditions may be of independent interest. In particular, the stability criterion of the multiserver model can be used for the capacity planning of the model at the design stage to obtain the lower bound of the capacity that keeps system stable. As an example of applications of our results, we estimate the carrying capacity of the automobile road, intersected by a crosswalk. Under capacity we mean the upper bound of the intensity of the flow of cars when the queue of cars does not tend to infinity. This means that the analysis can be based on the results obtained in this chapter.
We begin from the definition of the regenerative flow (Afanasyeva and Bashtova 2014)). Assume a stochastic process { X ( t ), t ≥ 0} ( X (0) = 0) taking values 0, 1, 2... to be defined in a probability space 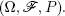 The process has non-decreasing and right-continuous sample paths. There exists filtration
The process has non-decreasing and right-continuous sample paths. There exists filtration 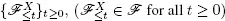 exists such that X is measurable with respect to
exists such that X is measurable with respect to 
DEFINITION 1.1.– The stochastic flow X is called regenerative if there is an increasing sequence of Markov moments with respect to such that the sequence
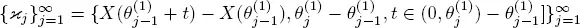
consists of independent identically distributed (iid) random elements on 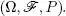
The random variable 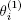 is said to be the i th regeneration point of X and
is said to be the i th regeneration point of X and 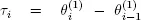 is the i th regeneration period
is the i th regeneration period 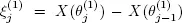 Let
Let 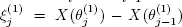 be the number of customers arrived during the j th regeneration period. Assume that
be the number of customers arrived during the j th regeneration period. Assume that 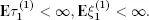 The limit
The limit 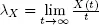 with probability 1 (w.p.1) is called the rate of X . It is easy to prove that
with probability 1 (w.p.1) is called the rate of X . It is easy to prove that  (Smith 1955; Thorisson 2000). The class of regenerative flows contains most of fundamental flows that are exploited in the queueing theory. First of all, the doubly stochastic Poisson process (Grandell 1976) with a regenerative process as a stochastic intensity is a regenerative flow. There are many other examples of regenerative flows, for instance, semi-Markovian, Markov-arrival, Markov- modulated and other processes (Afanasyeva and Tkachenko 2012).
(Smith 1955; Thorisson 2000). The class of regenerative flows contains most of fundamental flows that are exploited in the queueing theory. First of all, the doubly stochastic Poisson process (Grandell 1976) with a regenerative process as a stochastic intensity is a regenerative flow. There are many other examples of regenerative flows, for instance, semi-Markovian, Markov-arrival, Markov- modulated and other processes (Afanasyeva and Tkachenko 2012).
We consider discrete-time queueing systems as well as continuous-time queueing systems (Avi-Itzhak and Naor 1963). In the first case, time is divided into fixed length intervals or slots and all arrivals and departures are synchronized with respect to slot boundaries. Moreover, in the case of some events being synchronized at one slot these events are ordered as follows: arrival and departure. The system is observed at the end of the slot.
We consider a queueing system S with m servers, FCFS discipline and regenerative input flow X . We assume that a server may simultaneously serve only one customer so that at any time the number of customers on the servers is not more than m . A customer leaves a system only after completion the service. The system is defined by the sequence 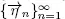 consisting of iid random vectors and multidimensional stochastic process
consisting of iid random vectors and multidimensional stochastic process 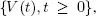 which are independent of the input flow X . The vector
which are independent of the input flow X . The vector 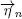 determines the characteristics of the n th customer, that is service times by various servers or necessary number of servers for service. The process V describes the states of the servers. For example, for the systems with unreliable servers this process defines the moments of breakdowns and restorations of the servers. The state of the system at time t is described by the stochastic process
determines the characteristics of the n th customer, that is service times by various servers or necessary number of servers for service. The process V describes the states of the servers. For example, for the systems with unreliable servers this process defines the moments of breakdowns and restorations of the servers. The state of the system at time t is described by the stochastic process 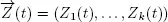 where one of the coordinates is the number of customers in the system. We assume that the relation
where one of the coordinates is the number of customers in the system. We assume that the relation
Читать дальше

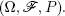 The process has non-decreasing and right-continuous sample paths. There exists filtration
The process has non-decreasing and right-continuous sample paths. There exists filtration 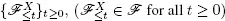 exists such that X is measurable with respect to
exists such that X is measurable with respect to 
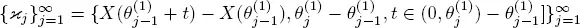
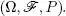
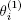 is said to be the i th regeneration point of X and
is said to be the i th regeneration point of X and 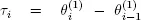 is the i th regeneration period
is the i th regeneration period 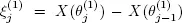 Let
Let 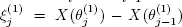 be the number of customers arrived during the j th regeneration period. Assume that
be the number of customers arrived during the j th regeneration period. Assume that 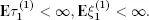 The limit
The limit 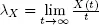 with probability 1 (w.p.1) is called the rate of X . It is easy to prove that
with probability 1 (w.p.1) is called the rate of X . It is easy to prove that  (Smith 1955; Thorisson 2000). The class of regenerative flows contains most of fundamental flows that are exploited in the queueing theory. First of all, the doubly stochastic Poisson process (Grandell 1976) with a regenerative process as a stochastic intensity is a regenerative flow. There are many other examples of regenerative flows, for instance, semi-Markovian, Markov-arrival, Markov- modulated and other processes (Afanasyeva and Tkachenko 2012).
(Smith 1955; Thorisson 2000). The class of regenerative flows contains most of fundamental flows that are exploited in the queueing theory. First of all, the doubly stochastic Poisson process (Grandell 1976) with a regenerative process as a stochastic intensity is a regenerative flow. There are many other examples of regenerative flows, for instance, semi-Markovian, Markov-arrival, Markov- modulated and other processes (Afanasyeva and Tkachenko 2012).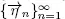 consisting of iid random vectors and multidimensional stochastic process
consisting of iid random vectors and multidimensional stochastic process 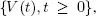 which are independent of the input flow X . The vector
which are independent of the input flow X . The vector 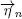 determines the characteristics of the n th customer, that is service times by various servers or necessary number of servers for service. The process V describes the states of the servers. For example, for the systems with unreliable servers this process defines the moments of breakdowns and restorations of the servers. The state of the system at time t is described by the stochastic process
determines the characteristics of the n th customer, that is service times by various servers or necessary number of servers for service. The process V describes the states of the servers. For example, for the systems with unreliable servers this process defines the moments of breakdowns and restorations of the servers. The state of the system at time t is described by the stochastic process 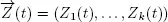 where one of the coordinates is the number of customers in the system. We assume that the relation
where one of the coordinates is the number of customers in the system. We assume that the relation










