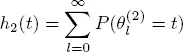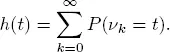[1.1] 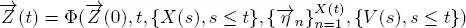
takes place for some function Φ( ∙ ) on the corresponding space. For example, for the system Reg| G |1| ∞ we consider the process 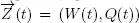 where W ( t ) is the virtual waiting time and Q ( t ) is the number of customers in the system at time t . Let
where W ( t ) is the virtual waiting time and Q ( t ) is the number of customers in the system at time t . Let 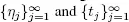 be the sequences of service and arrival times of customers, respectively, and
be the sequences of service and arrival times of customers, respectively, and 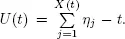 Assuming that Q (0) = 0, we have W ( t ) =
Assuming that Q (0) = 0, we have W ( t ) = 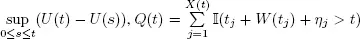 where
where 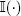 is an indicator function (Borovkov 1976).
is an indicator function (Borovkov 1976).
The main goal of this chapter is the determination of the conditions of the stochastic boundedness of the number of customers Q ( t ) in the system as t → ∞ . Our analysis is based on the construction of the auxiliary service process.
1.3. Auxiliary service process
For the system S , we define an auxiliary system S 0with input flow X 0such that when the number of customers in the system becomes less than m a new customer immediately arrives in the system. Therefore, there are always customers for service in S 0. Other characteristics such as the initial state, the sequence 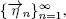 stochastic process
stochastic process 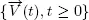 and a functional Φ are the same as for the system S . If in the system S the initial number of customers Q (0) < m , then the process X 0has the jump m – Q (0) at zero instant. We determine an auxiliary service process Y ( t ) as the number of customers served in S 0during (0 , t ). Since the flow Y is defined by the processes
and a functional Φ are the same as for the system S . If in the system S the initial number of customers Q (0) < m , then the process X 0has the jump m – Q (0) at zero instant. We determine an auxiliary service process Y ( t ) as the number of customers served in S 0during (0 , t ). Since the flow Y is defined by the processes 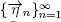 and V and these processes do not depend on the input flow X at the system S , we conclude that X and Y are independent flows.
and V and these processes do not depend on the input flow X at the system S , we conclude that X and Y are independent flows.
We also need additional assumptions.
CONDITION 1.1.– For the continuous-time case, Y is a strongly regenerative flow with the sequence 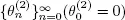 as points of regeneration.
as points of regeneration.
We call the regenerative flow Y strongly regenerative if the regeneration period 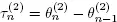 has the form
has the form
[1.2] 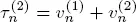
where 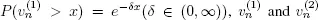 are independent random variables and
are independent random variables and 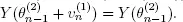
CONDITION 1.2.– For the discrete-time case, processes X and Y are regenerative aperiodic flows. As usually, aperiodicity means that the greatest common divisor (GCD)
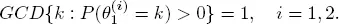
Then we may determine common points of regeneration 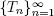 for both processes X and Y letting in the discrete-time case
for both processes X and Y letting in the discrete-time case
[1.3] 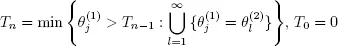
and in the continuous-time case
[1.4] 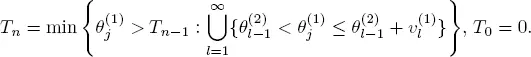
LEMMA 1.1.– Let for the continuous-time (discrete-time) condition 1.1 (condition 1.2) be fulfilled. Then the sequence 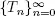 consists of common regeneration points for X and Y and
consists of common regeneration points for X and Y and
[1.5] 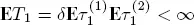
for the continuous-time case,
[1.6] 
for the discrete-time case.
PROOF.– Since the proof of [1.5]is almost the same as the proof of [1.6], we consider the discrete-time case only. Let
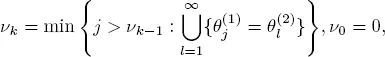
so that 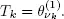 Then
Then 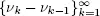 is a sequence of iid random variables and in accordance with Wald’s identity
is a sequence of iid random variables and in accordance with Wald’s identity 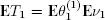 (Feller 1971). Therefore, we need to prove the finiteness of Eν1 . Denote by h 2( t ) ( h ( t )) the mean number of renewals at time t for the renewal process
(Feller 1971). Therefore, we need to prove the finiteness of Eν1 . Denote by h 2( t ) ( h ( t )) the mean number of renewals at time t for the renewal process 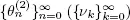 so that
so that
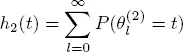
and
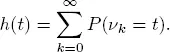
Taking into account condition 1.2, we derive from Blackwell’s theorem (Thorisson 2000)
Читать дальше

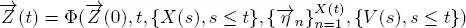
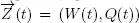 where W ( t ) is the virtual waiting time and Q ( t ) is the number of customers in the system at time t . Let
where W ( t ) is the virtual waiting time and Q ( t ) is the number of customers in the system at time t . Let 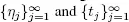 be the sequences of service and arrival times of customers, respectively, and
be the sequences of service and arrival times of customers, respectively, and 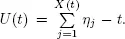 Assuming that Q (0) = 0, we have W ( t ) =
Assuming that Q (0) = 0, we have W ( t ) = 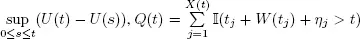 where
where 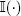 is an indicator function (Borovkov 1976).
is an indicator function (Borovkov 1976).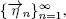 stochastic process
stochastic process 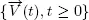 and a functional Φ are the same as for the system S . If in the system S the initial number of customers Q (0) < m , then the process X 0has the jump m – Q (0) at zero instant. We determine an auxiliary service process Y ( t ) as the number of customers served in S 0during (0 , t ). Since the flow Y is defined by the processes
and a functional Φ are the same as for the system S . If in the system S the initial number of customers Q (0) < m , then the process X 0has the jump m – Q (0) at zero instant. We determine an auxiliary service process Y ( t ) as the number of customers served in S 0during (0 , t ). Since the flow Y is defined by the processes 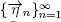 and V and these processes do not depend on the input flow X at the system S , we conclude that X and Y are independent flows.
and V and these processes do not depend on the input flow X at the system S , we conclude that X and Y are independent flows.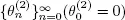 as points of regeneration.
as points of regeneration.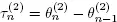 has the form
has the form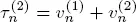
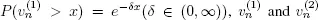 are independent random variables and
are independent random variables and 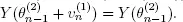
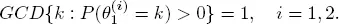
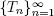 for both processes X and Y letting in the discrete-time case
for both processes X and Y letting in the discrete-time case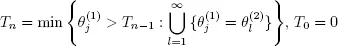
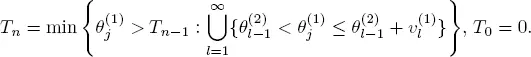
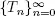 consists of common regeneration points for X and Y and
consists of common regeneration points for X and Y and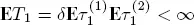

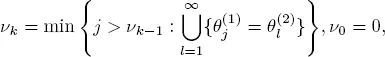
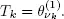 Then
Then 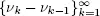 is a sequence of iid random variables and in accordance with Wald’s identity
is a sequence of iid random variables and in accordance with Wald’s identity 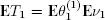 (Feller 1971). Therefore, we need to prove the finiteness of Eν1 . Denote by h 2( t ) ( h ( t )) the mean number of renewals at time t for the renewal process
(Feller 1971). Therefore, we need to prove the finiteness of Eν1 . Denote by h 2( t ) ( h ( t )) the mean number of renewals at time t for the renewal process 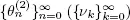 so that
so that