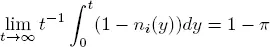
then 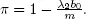 Therefore, the traffic rate for low priority customers has the form
Therefore, the traffic rate for low priority customers has the form
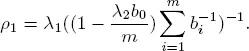
From corollary 1.1 we obtain corollary 1.3.
COROLLARY 1.3.– Assume that X 2is a strongly regenerative flow, B 0satisfies [1.14]and 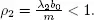 Then
Then 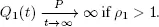 If additionally Bi satisfies [1.14]and ρ 1< 1, then Q 1( t ) is a stable process.
If additionally Bi satisfies [1.14]and ρ 1< 1, then Q 1( t ) is a stable process.
The first statement follows from corollary 1.1 since 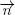 is a strongly regenerative process. To prove the second statement, we note that Q 2is a regenerative process and its stochastic boundedness means stability.
is a strongly regenerative process. To prove the second statement, we note that Q 2is a regenerative process and its stochastic boundedness means stability.
1.9. Queueing system with simultaneous service of a customer by a random number of servers
Here, we consider a system S assuming that the n th customer requires service from ζn server simultaneously 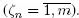 The customer arrived in an empty queue begins service immediately if the number of available servers is more or equal ζn . Otherwise the customer becomes the first in a queue and the service begins when the required number of servers becomes available. A customer who arrives in an nonempty queue takes the last place in the queue. When service begins, each server’s completion time is independent of all other servers and has an exponential distribution with rate μ . The sequence
The customer arrived in an empty queue begins service immediately if the number of available servers is more or equal ζn . Otherwise the customer becomes the first in a queue and the service begins when the required number of servers becomes available. A customer who arrives in an nonempty queue takes the last place in the queue. When service begins, each server’s completion time is independent of all other servers and has an exponential distribution with rate μ . The sequence 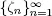 consists of iid random variables and
consists of iid random variables and 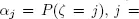
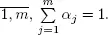 .
.
Queueing systems with simultaneous service have been studied in a number of works (Rumyantsev and Morozov 2017; and references therein). The stability conditions in an explicit form have been obtained for systems with a Poisson input flow and independent exponentially distributed service times by (Gillent and Latouche 1983). The main goal of this section is an extension of the stability condition to the model with a regenerative input flow X based on theorems 1.1 and 1.2. Thus, we consider the system S described in section 1.2with 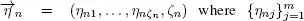 is a sequence of independent exponentially distributed random variables not depending on ζn . Let S 0be an auxiliary system defined in section 1.3. Instead of the process Y we consider the auxiliary flow Z that is the number of service completions by all m servers up to time t in the auxiliary system S 0. Denote by U ( t ) the number of occupied servers at time t in the system S 0. Then U is a Markov chain and Z is a doubly stochastic Poisson process (Grandell 1976) with a random intensity
is a sequence of independent exponentially distributed random variables not depending on ζn . Let S 0be an auxiliary system defined in section 1.3. Instead of the process Y we consider the auxiliary flow Z that is the number of service completions by all m servers up to time t in the auxiliary system S 0. Denote by U ( t ) the number of occupied servers at time t in the system S 0. Then U is a Markov chain and Z is a doubly stochastic Poisson process (Grandell 1976) with a random intensity 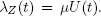 We note that the process U hits the state { m } from any state j = 1, 2 ,..., m with a positive probability. It means that all states attainable from the state { m } constitute the finite class K of communicating states. Therefore, there are limits
We note that the process U hits the state { m } from any state j = 1, 2 ,..., m with a positive probability. It means that all states attainable from the state { m } constitute the finite class K of communicating states. Therefore, there are limits
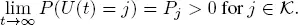
Let 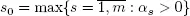 and
and 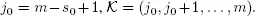
We have the system of equations for 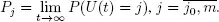
[1.18] 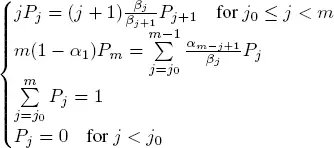
where  We may easily verify that the solution of [1.18]has the form
We may easily verify that the solution of [1.18]has the form
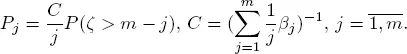
Since
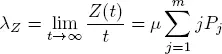
we get
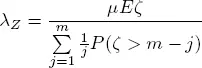
and the traffic rate for the system S
[1.19] 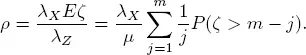
Let us note that this formula is the same as obtained by (Gillent and Latouche 1983) for queueing systems with a Poisson input flow. To employ theorems 1.1 and 1.2, we have to verify conditions 1.1, 1.3, 1.4 and 1.5. First of all we note that Z is a strongly regenerative flow. As points of regeneration, we may take the sequential hitting times 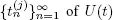 into the fixed state
into the fixed state 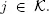 (We take
(We take 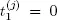 if
if 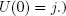 Then
Then 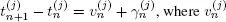 is the sojourn time in the state j and
is the sojourn time in the state j and 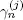 is the return time to this state after exit from it for U(t) . The random variables
is the return time to this state after exit from it for U(t) . The random variables 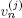 and
and 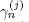 are independent and
are independent and 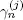 has an exponential distribution. Moreover,
has an exponential distribution. Moreover, 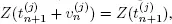 therefore, condition 1.1 holds. Let q ( t ) be the total number of servers that are already busy or will be busy by service of the Q ( t ) customers, which are present at the system S at time t . Then q ( t ) as well as Q ( t ) is a regenerative process with a sequence
therefore, condition 1.1 holds. Let q ( t ) be the total number of servers that are already busy or will be busy by service of the Q ( t ) customers, which are present at the system S at time t . Then q ( t ) as well as Q ( t ) is a regenerative process with a sequence 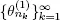 of points of regeneration that is a subsequence of
of points of regeneration that is a subsequence of 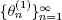 such that
such that 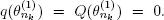 Let us recall that
Let us recall that 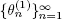 is a sequence of points of regeneration for X . Therefore, because of theorem 1 from (Afanasyeva and Tkachenko 2014), condition 1.4 is fulfilled. Now for any fix
is a sequence of points of regeneration for X . Therefore, because of theorem 1 from (Afanasyeva and Tkachenko 2014), condition 1.4 is fulfilled. Now for any fix 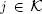 we define the common points of regeneration
we define the common points of regeneration 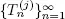 for the input flow X and auxiliary flow Z by the relation
for the input flow X and auxiliary flow Z by the relation
Читать дальше

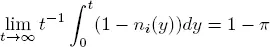
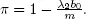 Therefore, the traffic rate for low priority customers has the form
Therefore, the traffic rate for low priority customers has the form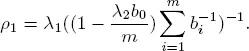
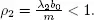 Then
Then 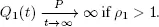 If additionally Bi satisfies [1.14]and ρ 1< 1, then Q 1( t ) is a stable process.
If additionally Bi satisfies [1.14]and ρ 1< 1, then Q 1( t ) is a stable process.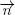 is a strongly regenerative process. To prove the second statement, we note that Q 2is a regenerative process and its stochastic boundedness means stability.
is a strongly regenerative process. To prove the second statement, we note that Q 2is a regenerative process and its stochastic boundedness means stability.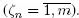 The customer arrived in an empty queue begins service immediately if the number of available servers is more or equal ζn . Otherwise the customer becomes the first in a queue and the service begins when the required number of servers becomes available. A customer who arrives in an nonempty queue takes the last place in the queue. When service begins, each server’s completion time is independent of all other servers and has an exponential distribution with rate μ . The sequence
The customer arrived in an empty queue begins service immediately if the number of available servers is more or equal ζn . Otherwise the customer becomes the first in a queue and the service begins when the required number of servers becomes available. A customer who arrives in an nonempty queue takes the last place in the queue. When service begins, each server’s completion time is independent of all other servers and has an exponential distribution with rate μ . The sequence 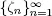 consists of iid random variables and
consists of iid random variables and 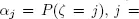
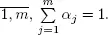 .
.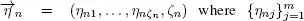 is a sequence of independent exponentially distributed random variables not depending on ζn . Let S 0be an auxiliary system defined in section 1.3. Instead of the process Y we consider the auxiliary flow Z that is the number of service completions by all m servers up to time t in the auxiliary system S 0. Denote by U ( t ) the number of occupied servers at time t in the system S 0. Then U is a Markov chain and Z is a doubly stochastic Poisson process (Grandell 1976) with a random intensity
is a sequence of independent exponentially distributed random variables not depending on ζn . Let S 0be an auxiliary system defined in section 1.3. Instead of the process Y we consider the auxiliary flow Z that is the number of service completions by all m servers up to time t in the auxiliary system S 0. Denote by U ( t ) the number of occupied servers at time t in the system S 0. Then U is a Markov chain and Z is a doubly stochastic Poisson process (Grandell 1976) with a random intensity 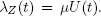 We note that the process U hits the state { m } from any state j = 1, 2 ,..., m with a positive probability. It means that all states attainable from the state { m } constitute the finite class K of communicating states. Therefore, there are limits
We note that the process U hits the state { m } from any state j = 1, 2 ,..., m with a positive probability. It means that all states attainable from the state { m } constitute the finite class K of communicating states. Therefore, there are limits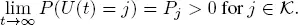
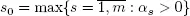 and
and 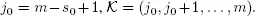
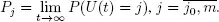
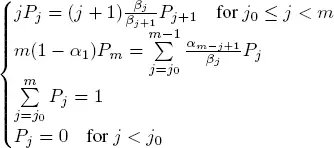
 We may easily verify that the solution of [1.18]has the form
We may easily verify that the solution of [1.18]has the form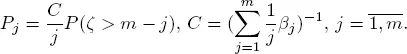
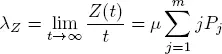
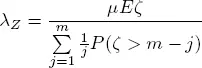
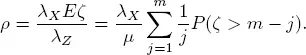
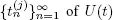 into the fixed state
into the fixed state 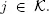 (We take
(We take 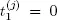 if
if 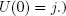 Then
Then 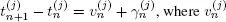 is the sojourn time in the state j and
is the sojourn time in the state j and 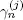 is the return time to this state after exit from it for U(t) . The random variables
is the return time to this state after exit from it for U(t) . The random variables 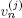 and
and 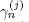 are independent and
are independent and 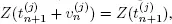 therefore, condition 1.1 holds. Let q ( t ) be the total number of servers that are already busy or will be busy by service of the Q ( t ) customers, which are present at the system S at time t . Then q ( t ) as well as Q ( t ) is a regenerative process with a sequence
therefore, condition 1.1 holds. Let q ( t ) be the total number of servers that are already busy or will be busy by service of the Q ( t ) customers, which are present at the system S at time t . Then q ( t ) as well as Q ( t ) is a regenerative process with a sequence 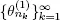 of points of regeneration that is a subsequence of
of points of regeneration that is a subsequence of 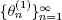 such that
such that 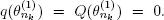 Let us recall that
Let us recall that 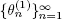 is a sequence of points of regeneration for X . Therefore, because of theorem 1 from (Afanasyeva and Tkachenko 2014), condition 1.4 is fulfilled. Now for any fix
is a sequence of points of regeneration for X . Therefore, because of theorem 1 from (Afanasyeva and Tkachenko 2014), condition 1.4 is fulfilled. Now for any fix 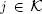 we define the common points of regeneration
we define the common points of regeneration 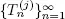 for the input flow X and auxiliary flow Z by the relation
for the input flow X and auxiliary flow Z by the relation










