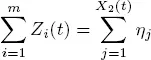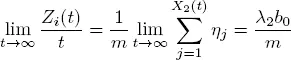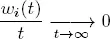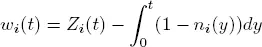For any aperiodic class 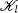 of states based on Foster’s criterion (Meyn and Tweedie 2009), we may easily prove that this class is ergodic (Afanasyeva and Tkachenko 2016, 2018). Therefore, the process Qn is stochastically bounded if
of states based on Foster’s criterion (Meyn and Tweedie 2009), we may easily prove that this class is ergodic (Afanasyeva and Tkachenko 2016, 2018). Therefore, the process Qn is stochastically bounded if 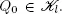 It is also true if
It is also true if 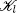 is a periodic class. Since the number of classes r < ∞, we obtain the stochastic boundedness of the process Qn and therefore Q(t) .
is a periodic class. Since the number of classes r < ∞, we obtain the stochastic boundedness of the process Qn and therefore Q(t) .
We may obtain the upper bound of the traffic rate ρ providing the stochastic boundedness of the process Q . It is known from (Borovkov 1976) that
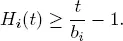
Therefore
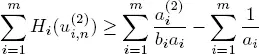
and sufficient condition of the stochastic boundedness of Q has the following form
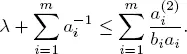
If bi = b , then we have the same condition as obtained in Morozov et al . (2011) ■
1.8. Queueing system with a preemptive priority discipline
In this section we study a continuous-time queueing system with two independent regenerative input flows X 1and X 2with intensities λ 1and λ 2and m servers. The customers of the second type (which belong to X 2) have an absolute priority with respect to customers of the first type. Service interruption for the low priority customer occurs when a high priority customer arrives during a low priority customer’s service time. If at an arrival time of the second type customer there are m 1free servers, m 2servers occupied by customers of the first type and m – m 1– m 2servers occupied by customers of the second type, then an arriving customer randomly chooses any server from m 1+ m 2servers, which are not busy by customers of the second type. Service times by the i th server for high(low) priority customers have distribution function B 0 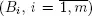 with mean
with mean 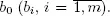 Therefore, for high priority customers we have a system Reg|G|m with homogeneous servers and for low priority customers a system with interruptions and preemptive resume service discipline considered in section 1.6.
Therefore, for high priority customers we have a system Reg|G|m with homogeneous servers and for low priority customers a system with interruptions and preemptive resume service discipline considered in section 1.6.
Denote by Qi ( t ) the number of customers of the i th type at the system including the customers on the servers at time 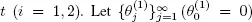 and
and 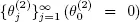 be the sequences of regeneration points for X 1and X 2, respectively. Under some additional conditions, for example, when the inequality [1.14]is valid for the function B 0(other sufficient assumptions are given in Afanasyeva and Tkachenko (2014)), the process Q 2is regenerative with points of regeneration
be the sequences of regeneration points for X 1and X 2, respectively. Under some additional conditions, for example, when the inequality [1.14]is valid for the function B 0(other sufficient assumptions are given in Afanasyeva and Tkachenko (2014)), the process Q 2is regenerative with points of regeneration
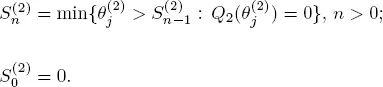
The stability condition for the process Q 2has the form (Afanasyeva and Tkachenko 2014)
[1.17] 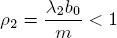
that is supposed to be fulfilled. We now want to get the stability condition for the process Q 1.
We start with the definition of the process of interruptions. Let ni ( t ) =0 if at instant t the i th server is occupied by a high priority customer and ni(t) = 1 otherwise, 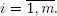 As regeneration points for
As regeneration points for 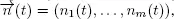 , we take subsequence
, we take subsequence 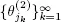 of the regeneration points sequence
of the regeneration points sequence 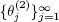 for the input flow X 2such that
for the input flow X 2such that 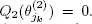 As before, we assume that [1.14]holds for B 0. Since X 2is a strongly regenerative flow, condition 1.6 is fulfilled.
As before, we assume that [1.14]holds for B 0. Since X 2is a strongly regenerative flow, condition 1.6 is fulfilled.
To obtain the traffic rate for low priority customers, we need to find 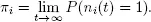 Because of the rule of the server choose by an arriving high priority customer, we have
Because of the rule of the server choose by an arriving high priority customer, we have 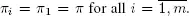 for all
for all 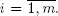 To calculate π , we define for high priority customers the following processes. Let wi ( t ) be the residual service time (virtual waiting time) on the i th server at instant t and Zi ( t ) the total service time of customers which arrived up to time t and have to be served on the i th server. Thus
To calculate π , we define for high priority customers the following processes. Let wi ( t ) be the residual service time (virtual waiting time) on the i th server at instant t and Zi ( t ) the total service time of customers which arrived up to time t and have to be served on the i th server. Thus
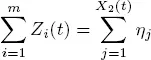
where ηj is the service time of the j th arrived customer. We note that w.p.1
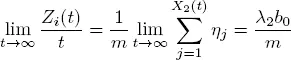
and
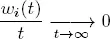
because of the stability condition [1.17].
Since
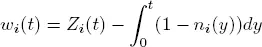
and w.p.1
Читать дальше

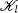 of states based on Foster’s criterion (Meyn and Tweedie 2009), we may easily prove that this class is ergodic (Afanasyeva and Tkachenko 2016, 2018). Therefore, the process Qn is stochastically bounded if
of states based on Foster’s criterion (Meyn and Tweedie 2009), we may easily prove that this class is ergodic (Afanasyeva and Tkachenko 2016, 2018). Therefore, the process Qn is stochastically bounded if 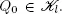 It is also true if
It is also true if 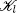 is a periodic class. Since the number of classes r < ∞, we obtain the stochastic boundedness of the process Qn and therefore Q(t) .
is a periodic class. Since the number of classes r < ∞, we obtain the stochastic boundedness of the process Qn and therefore Q(t) .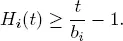
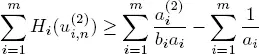
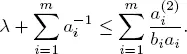
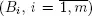 with mean
with mean 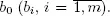 Therefore, for high priority customers we have a system Reg|G|m with homogeneous servers and for low priority customers a system with interruptions and preemptive resume service discipline considered in section 1.6.
Therefore, for high priority customers we have a system Reg|G|m with homogeneous servers and for low priority customers a system with interruptions and preemptive resume service discipline considered in section 1.6.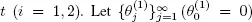 and
and 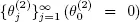 be the sequences of regeneration points for X 1and X 2, respectively. Under some additional conditions, for example, when the inequality [1.14]is valid for the function B 0(other sufficient assumptions are given in Afanasyeva and Tkachenko (2014)), the process Q 2is regenerative with points of regeneration
be the sequences of regeneration points for X 1and X 2, respectively. Under some additional conditions, for example, when the inequality [1.14]is valid for the function B 0(other sufficient assumptions are given in Afanasyeva and Tkachenko (2014)), the process Q 2is regenerative with points of regeneration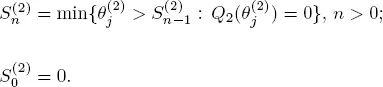
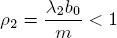
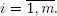 As regeneration points for
As regeneration points for 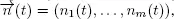 , we take subsequence
, we take subsequence 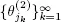 of the regeneration points sequence
of the regeneration points sequence 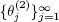 for the input flow X 2such that
for the input flow X 2such that 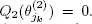 As before, we assume that [1.14]holds for B 0. Since X 2is a strongly regenerative flow, condition 1.6 is fulfilled.
As before, we assume that [1.14]holds for B 0. Since X 2is a strongly regenerative flow, condition 1.6 is fulfilled.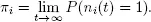 Because of the rule of the server choose by an arriving high priority customer, we have
Because of the rule of the server choose by an arriving high priority customer, we have 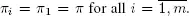 for all
for all 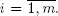 To calculate π , we define for high priority customers the following processes. Let wi ( t ) be the residual service time (virtual waiting time) on the i th server at instant t and Zi ( t ) the total service time of customers which arrived up to time t and have to be served on the i th server. Thus
To calculate π , we define for high priority customers the following processes. Let wi ( t ) be the residual service time (virtual waiting time) on the i th server at instant t and Zi ( t ) the total service time of customers which arrived up to time t and have to be served on the i th server. Thus