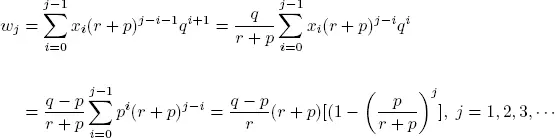It is known that for a stable system, there exists a matrix R , with spectral radius less than 1, which is the minimal non-negative solution of the matrix quadratic equation
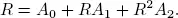
The R matrix has a counterpart stochastic matrix G for a stable system, a minimal non-negative solution to the matrix quadratic equation

and there is a simple relationship between the two as follows
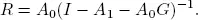
Given the matrix R , we can then use the matrix-geometric results of Neuts (1981) to obtain
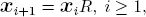
after solving for the boundary equations as
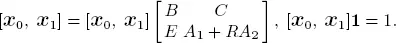
This is then normalized by 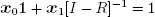 .
.
As one sees the matrix, R could be of huge dimension, so solving it using the well-known methods could still be time consuming. However, because of the structure presented by the matrix G , we could exploit it and then obtain R directly from G . Due to the structure of the matrix A 2, we see that the matrix G has only one column block of non-zero matrix, hence the computation of matrix G is more efficient. The matrix is of the form

In what follows, we present a case of a single-server queueing model in discrete time, with interdependent interarrival and service times based on bivariate geometric distribution.
1.5. Interdependent interarrival and service times
Chao (1995) discussed the case of bivariate exponential distributions for joint interarrival and service times queues and showed the waiting time is monotonically decreasing in the dependency in increasing convex ordering sense. sun and Basu (1995) introduced a class of bivariate geometric distribution originally presented by Hawkes (1972). Omey and Minkova (2013) presented a bivariate geometric distribution, which we extend to the general matrix structure. In what follows, we consider the case where the service and the interarrival times are interdependent and represented by a bivariate geometric distribution as in Omey and Minkova (2013).
Omey and Minkova (2013) consider a bivariate geometric distribution described by two random variables X (with two possible states S1 , S2 ) and F · S1 is success of type 1 and S 2is success of type 2, and F is a failure. Let
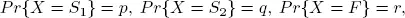
where 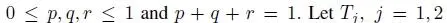 be defined as
be defined as 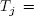
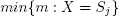 , then
, then
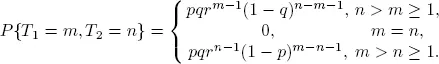
It is straightforward to see that if r is fixed, then as p increases q decreases and vice versa. Hence, there is negative correlation between type 1 and type 2 successes in that case. Equally, if we say p is fixed, then q can be allowed to increase or decrease at the expense of r . These types of effects of interarrival and service times have not received much attention in queueing theory; 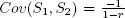 . This makes sense as an increase in S1 leads to a decrease in S2 and vice versa.
. This makes sense as an increase in S1 leads to a decrease in S2 and vice versa.
1.5.1. A discrete time queueing model with bivariate geometric distribution
If we study a single-server queue in discrete time, with success of type 1 signifying an arrival and type 2 a service completion if there is a customer in the system, and letting a failure represent no event. Then keeping in mind that the event of having both type 1 and type 2 successes at the same time is zero, then our DTMC is
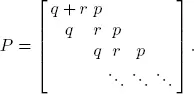
The system is stable if p < q . Letting the number in the system at steady state be X and defining 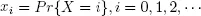 with
with  , then we have
, then we have
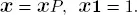
Letting 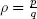 we end up with
we end up with

Letting  , we have
, we have

and
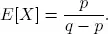
REMARK 1.4.– The bivariate geometric distribution is the discrete analogue of the bivariate exponential distribution. From the result of the mean number in the system, it is clear that by holding q constant and varying r, this mean is monotonically decreasing in the dependency in increasing convex ordering sense as expected. It is conjectured that this is also transferrable to the mean waiting time .
Let W be the waiting time in the system, i.e. the time spent waiting in the queue, plus the service time. If we define 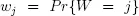 , then the waiting time distribution can be written as
, then the waiting time distribution can be written as
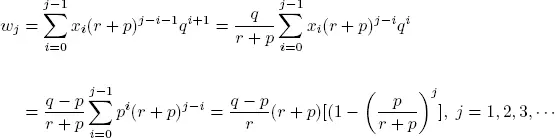
1.5.2. Matrix equivalent model
Читать дальше

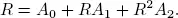

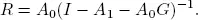
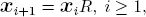
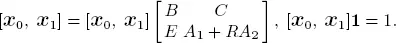
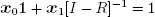 .
.
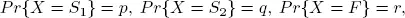
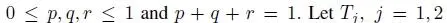 be defined as
be defined as 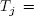
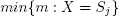 , then
, then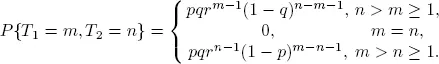
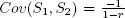 . This makes sense as an increase in S1 leads to a decrease in S2 and vice versa.
. This makes sense as an increase in S1 leads to a decrease in S2 and vice versa.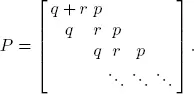
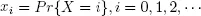 with
with  , then we have
, then we have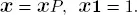
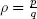 we end up with
we end up with
 , we have
, we have
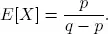
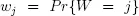 , then the waiting time distribution can be written as
, then the waiting time distribution can be written as