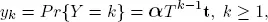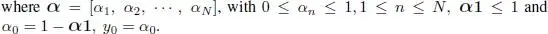1) if then E(X(b)) will be decreasing as b increases;
2) if then E(X(b)) will be increasing as b increases.
The first part of proposition 1.3 is straightforward in that an increase in the service rate reduces the arrival, thereby reducing the traffic intensity and decreasing the expected number in the system. However, an increase to the service rate could also lead to an increase in the mean number in the system as observed in the second part of the proposition, which can be explained by the rate at which the arrival probability increases compared to the service completion probability ( b ), especially if that rate is high.
CASE 1 : Consider the case where f ( b ) is a decreasing function of b , say for example a = f ( b ) = 1 – b 2, with the strict condition that f ( b ) = 1 – b 2 < b . For this, we have
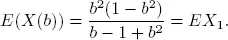
In this case, as b increases we see that E ( X ( b )) decreases as well. This is because the arrival probability decreases at a faster rate than service completion increases, i.e. f′ ( b ) = – 2 b .
REMARK 1.1.– For the case where a = f ( b ) = 1 – b 2, the arrival probability is a decreasing concave function of the service completion probability and the mean number in the system is decreasing in a convex form.
CASE 2 : Next consider the case where f ( b ) is an increasing function of b , say for example a = f ( b ) = b 2, with the strict condition that f ( b ) = b 2 < b . In this case, we have
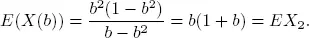
In this case, as b increases we see that E ( X ( b )) increases because the arrival probability increases faster than service completion increases, i.e. f′ ( b ) = 2 b .
REMARK 1.2.– For the case where a = f ( b ) = b 2, with arrival probability increasing in a convex form of the service completion probability, the mean number in the system increases in a convex form as well .
CASE 3 : Let us consider another case where f ( b ) is a linear decreasing function of b, say for example a = f ( b ) = 1 – b , with the strict condition that 1 – b < b . In this case, we have
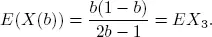
In this case, as b increases we see that decreases because the arrival probability is decreasing in the same rate as the service completion rate increases, i.e. 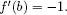
REMARK 1.3.– However, for the case where a= f(b) = 1-b, the arrival probability decreasing in a linear form of the service completion probability, the mean number in the system decreases in a strict convex form .
We summarize the results of the mean number in the system for the three cases in Table 1.1, with **** representing infeasible situations because the traffic intensity is greater than 1.
1.2.2. Service times dependent on interarrival times
The case of the Geo/Geo/1 system in which the service times depend on the interarrival times can be studied using the same idea and techniques as in section 1.2.1. If we define the arrival probability as a and the service time completion probability as b = g ( a ), it is straightforward to extend the ideas of that section directly. The queueing performance measures such as the mean number in the system, which we now define as E ( X ( a )) can be written as
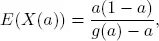
and the stability condition given as a < g ( a ). Since the procedures will be the same, they will not be discussed in this chapter.
Table 1.1. Mean number in system for the three cases
| b |
EX1 |
EX2 |
EX3 |
| 0.10 |
**** |
0.1100 |
**** |
| 0.20 |
**** |
0.2400 |
**** |
| 0.30 |
**** |
0.3900 |
**** |
| 0.40 |
**** |
0.5600 |
**** |
| 0.50 |
**** |
0.7500 |
**** |
| 0.60 |
**** |
0.9600 |
1.2000 |
| 0.70 |
1.3153 |
1.1900 |
0.5250 |
| 0.75 |
0.7875 |
1.3125 |
0.3750 |
| 0.80 |
0.5236 |
1.4400 |
0.2667 |
| 0.85 |
0.3502 |
1.5725 |
0.1821 |
| 0.90 |
0.2168 |
1.7100 |
0.1125 |
| 0.95 |
0.1032 |
1.8525 |
0.0528 |
In this section, the idea of Geo/Geo/1 system with interdependent interarrival and service times is generalized to the case of the PH/PH/1 system. However, first let us give a very brief review of the discrete PH distribution.
1.3.1. A review of discrete PH distribution
Consider a discrete time absorbing Markov chain with state space Xn , n = 0, 1, 2, ∙ ∙ ∙ , with Xn = 0, 1, 2, ∙ ∙ ∙ , N , where state 0 is an absorbing state. The transition matrix of this chain can be written as
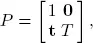
where 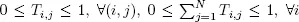 with
with 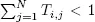 for at least one i. Also define t = 1 – T 1, where 1is a column of ones.
for at least one i. Also define t = 1 – T 1, where 1is a column of ones.
There is a discrete random variable Y , which is said to have a PH distribution ( α,T ) if one can write
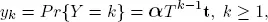
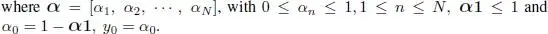
Several well-known discrete distributions can be represented as PH distributions. Examples include the geometric distribution, the negative binomial distribution, to name just a few. In addition, most discrete distributions can be reasonably approximated by discrete PH distribution (see Mészáros et al . 2014 and references therein).
Читать дальше

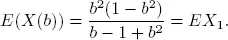
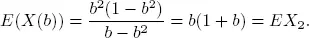
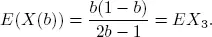
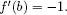
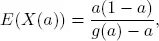
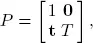
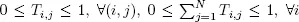 with
with 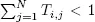 for at least one i. Also define t = 1 – T 1, where 1is a column of ones.
for at least one i. Also define t = 1 – T 1, where 1is a column of ones.