One of the most recent works on this subject is by Iyer and Manjunanth (2006) who also studied the interarrival and service times of queue by using mixtures of bivariates. Panda et al . (2017), in a work similar to the one by Iyer and Manunanth (2006), studied queues in which batch interarrival and service times are correlated by representing them with a bivariate mixture of rational ( R ) distributions.
Generally, most of the reported works focus on proportional relationships between interarrival times and service times. This is quite limiting. In this chapter, this aspect is relaxed, and the interdependence between the interarrival times and services is captured in a one-way dependence of interarrival time on service time and later in a two-way dependence. However, that dependence is allowed to be general. In the one-way case, we start by considering the Geo/Geo/1 system in which the arrival probability depends on service completion probability. Specifically in the general one-way case, we assume that there is a set of several, but finite, number of interarrival times. At the end of a service completion, the next interarrival time of a user is selected based on the service time. Even though the distributions of the interarrival times and service times will be general, we will be using the discrete phase type distribution to represent them based on the fact any discrete general distributions, with finite support, can be represented by a Markov chain (Alfa 2004).
Consider the simple Geo/Geo/1 system where the probability of arrival is a and of service completion is b . Let Xn ( a, b ), n = 0,1,2, ∙∙∙ be the number in the system at time n for a specified pair ( a, b ), with 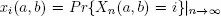 for the case of a stable system. Based on the results in Alfa (2016), the associated discrete time Markov chain (DTMC) has the transition matrix P written as
for the case of a stable system. Based on the results in Alfa (2016), the associated discrete time Markov chain (DTMC) has the transition matrix P written as
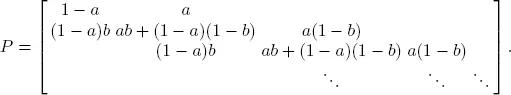
For a stable system with 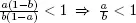 , we have
, we have
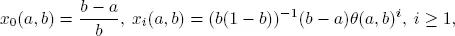
and
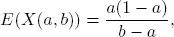
where 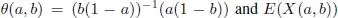 is the expected value of
is the expected value of 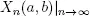 .
.
Next we consider the cases of a = f ( b ). We require that the following condition applies all the time in this section:
[1.1] 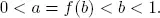
We consider two main cases: one when f (∙) is a decreasing function and the second one when it is an increasing function.
1.2.1. Arrival probability as a function of service completion probability
When we consider the case where a = f ( b ), we have
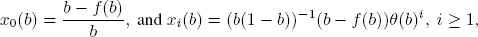
and
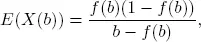
where 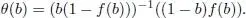
Next, we study the behavior of this system as a function of b .
1.2.1.1. Consider x 0( b )
By differentiating x 0( b ) with respect to b , we have
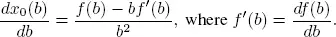
PROPOSITION 1.1.– By studying the derivative of x 0(b) w.r.t. b, we observe
1) if f’(b) is negative, then an increase in b leads to an increase in the probability that the system is empty;
2) if f’(b) is positive, then the probability that the system is empty could be increasing or decreasing, depending on whether respectively. Hence, an increase in the arrival rate as a function of the service rate does not necessarily mean a decrease in the emptiness probability.
We obtain additional information by considering the rate of increase in the probability of empty system as a rate of increase in the service completion probability, i.e.
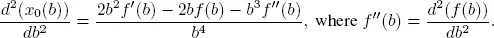
PROPOSITION 1.2.– If f ( b ) is convex and f ’( b ) < 0, then x 0( b ) is definitely concave. if f ( b ) is decreasing fast, then x 0(b) is increasing slowly, i.e. f ( b ) decreasing faster than increases. If, however, f ( b ) is convex and 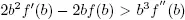 then x 0( b ) is convex.
then x 0( b ) is convex.
1.2.1.2. Consider E ( X ( b ))
Next let us consider E ( X ( b )). By differentiating E ( X ( b )) w.r.t. b , wehave
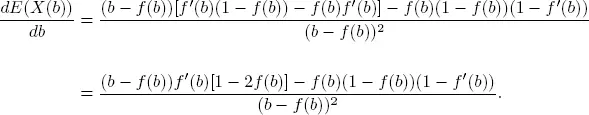
Define
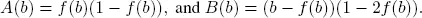
For a stable system, we know that b – f ( b ) and 1– f ( b ) are always positive, hence both A ( b ) and B ( b ) are always positive if 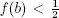 .
.
We thus have that the behavior of E ( X ( b )) depends entirely on f ’( b ), A ( b ) and B ( b ) and whether 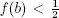 or not. E ( X ( b )) depends on the sign and values of the first three parameters, and the value of the fourth one.
or not. E ( X ( b )) depends on the sign and values of the first three parameters, and the value of the fourth one.
PROPOSITION 1.3.– For a stable system,
Читать дальше

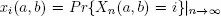 for the case of a stable system. Based on the results in Alfa (2016), the associated discrete time Markov chain (DTMC) has the transition matrix P written as
for the case of a stable system. Based on the results in Alfa (2016), the associated discrete time Markov chain (DTMC) has the transition matrix P written as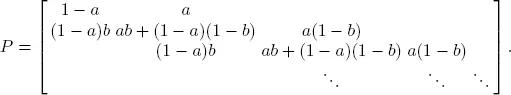
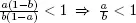 , we have
, we have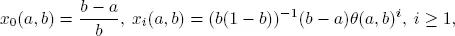
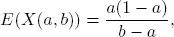
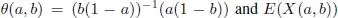 is the expected value of
is the expected value of 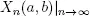 .
.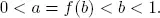
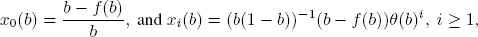
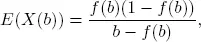
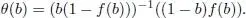
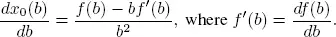
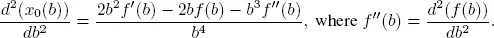
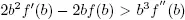 then x 0( b ) is convex.
then x 0( b ) is convex.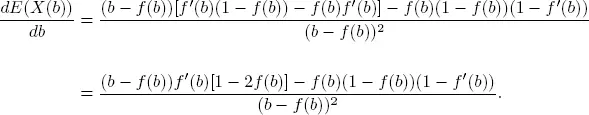
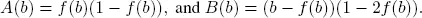
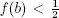 .
.










