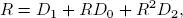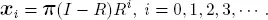Consider three square matrices D 0, D 1and D 2, with 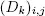 capturing the probability of transition from state i to state j , with k = 0, 1, 2 event occurring. The event 1 is type 1 success, event 2 is type 2 success and event 0 is no success of either type. We assume that the matrix D = D 0+ D 1+ D 2is a stochastic matrix, which is irreducible. Further, we define π = πD, π 1 = 1 . Keeping in mind that the event of having both type 1 and type 2 successes at the same time is zero, then our DTMC is
capturing the probability of transition from state i to state j , with k = 0, 1, 2 event occurring. The event 1 is type 1 success, event 2 is type 2 success and event 0 is no success of either type. We assume that the matrix D = D 0+ D 1+ D 2is a stochastic matrix, which is irreducible. Further, we define π = πD, π 1 = 1 . Keeping in mind that the event of having both type 1 and type 2 successes at the same time is zero, then our DTMC is
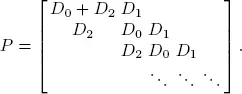
If the DTMC is positive recurrent, which we assume it is, then we have
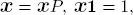
where 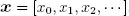 .
.
From the matrix-geometric theorem of Neuts (1981), we know that there is a matrix R , which is the minimal non-negative solution to the matrix quadratic equation
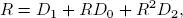
and because of the theorem and the special structure of the boundary of the DTMC we have
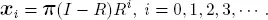
From this result, all the other performance measures such as the waiting time and busy period can be obtained.
In this chapter, we have introduced some queueing models that incorporate some form of interdependence between interarrival times and service times. We mainly considered the case where the interarrival times depend on the service times, before extending the idea to the interdependence of both. We show that the standard matrix-analytic methods can be used for analyzing such queues. Still there is a considerable amount of work to be done in the exact representations of the interdependencies when it comes to the phase type-based models. That will be the focus of future work on this subject.
The author thanks the reviewer for useful comments that have assisted in improving the presentation of the work. The author’s research is supported in part by the NRF (South Africa) SARChI ASN Chair programme.
Alfa, A.S. (2004). Markov chain representations of discrete time distributions applied to queueing models. Comp. Oper. Res ., 31, 2365–2385.
Alfa, A.S. (2016). Applied Discrete-Time Queues , 2nd edition. Springer, New York.
Benes, V.E. (1957). On queues with Poisson arrivals. Annal. Math. Statist ., 28(3), 670–677.
Benes, V.E. (1960). Combinatory methods and stochastic Kolmogorov Equations in the theory of queues. Trans. Amer. Math. Soc., 94(2), 282–294.
Chao, X. (1995). Monotone effect of dependency between interarrival and service times in a simple queueing system. Oper. Res. Lett ., 17, 47–51.
Cidon, I., Guerin, R., Khamisy, A., Sidi, M. (1993). Analysis of a correlated queue in a communication system. IEEE Trans. Inform. Theory , 39(2), 456–465.
Cidon, I., Guerin, R., Khamisy, A., Sidi, M. (1996). On queues with interarrival times proportional to service times. Probab. Eng. Inform. Sci ., 10, 87–107.
Graham, A. (1981). Kronecker Products and Matrix Calculus: With Applications . Dover Publications, New York.
Fendick, K.W., Saksena, V.R., Whitt, W. (1989). Dependence in packet queues. IEEE Trans. Commun ., 37(11), 1173–1183.
Hadidi, N. (1981a). Queues with partial correlation. SIAM J. Appl. Math ., 40, 467–475.
Hadidi, N. (1981b). Further result on queues with partial correlation. Oper. Res ., 33, 203–209.
Iyer, S.K., Manjunath, D. (2006). Queues with dependency between interarrival and service times using mixture of bivariates. Stoch. Model ., 22, 3–20.
John, F.L. (1963). Single server queues with dependent service and inter-arrival times. J. Soc. Indust. Appl. Math ., 11(3), 526–534.
Khatri, C.G., Rao, C.R. (1968). Solutions to some functional and their applications to characterization of probability distributions. Sankhya , 30, 167–180.
Mészáros, A., Papp, J., Telek, M. (2014). Fitting traffic traces with discrete canonical phase type distributions and Markov arrival processes. Int. J. Appl. Math. Comput. Sci ., 24(3), 453–470.
Muller, A. (2000). On the waiting times in queues with dependency between interarrival and service times. Oper. Res. Lett ., 26, 43–47.
Neuts, M.F. (1981). Matrix-geometric Solutions in Stochastic Models – An Algorithmic Approach . The Johns Hopkins University Press, Baltimore.
Omey, E., Minkova, L.D. (2013). Bivariate geometric distributions. HUB Research Papers 2013/02, Economics and Business Science . March.
Panda, G., Banik, A.D., Chaudhry, M.L. (2017). Stationary distributions of the R [X]/R/1 cross-correlated queue. Comm. Statistics – Theory and Methods , 46(17), 8666–8689.
Sun, K., Basu, A.P. (1995). A characterization of a bivariate geometric distribution. Stat. and Probabil. Lett ., 23, 307–311.
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.

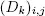 capturing the probability of transition from state i to state j , with k = 0, 1, 2 event occurring. The event 1 is type 1 success, event 2 is type 2 success and event 0 is no success of either type. We assume that the matrix D = D 0+ D 1+ D 2is a stochastic matrix, which is irreducible. Further, we define π = πD, π 1 = 1 . Keeping in mind that the event of having both type 1 and type 2 successes at the same time is zero, then our DTMC is
capturing the probability of transition from state i to state j , with k = 0, 1, 2 event occurring. The event 1 is type 1 success, event 2 is type 2 success and event 0 is no success of either type. We assume that the matrix D = D 0+ D 1+ D 2is a stochastic matrix, which is irreducible. Further, we define π = πD, π 1 = 1 . Keeping in mind that the event of having both type 1 and type 2 successes at the same time is zero, then our DTMC is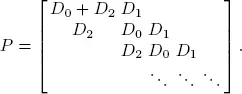
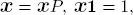
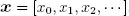 .
.