1 Cover
2 Title Page SCIENCES Mathematics , Field Director – Nikolaos Limnios Queuing Theory and Applications , Subject Head – Vladimir Anisimov
3 Copyright First published 2020 in Great Britain and the United States by ISTE Ltd and John Wiley & Sons, Inc. Apart from any fair dealing for the purposes of research or private study, or criticism or review, as permitted under the Copyright, Designs and Patents Act 1988, this publication may only be reproduced, stored or transmitted, in any form or by any means, with the prior permission in writing of the publishers, or in the case of reprographic reproduction in accordance with the terms and licenses issued by the CLA. Enquiries concerning reproduction outside these terms should be sent to the publishers at the undermentioned address: ISTE Ltd 27-37 St George’s Road London SW19 4EU UK www.iste.co.uk John Wiley & Sons, Inc. 111 River Street Hoboken, NJ 07030 USA www.wiley.com © ISTE Ltd 2020 The rights of Vladimir Anisimov and Nikolaos Limnios to be identified as the author of this work have been asserted by them in accordance with the Copyright, Designs and Patents Act 1988. Library of Congress Control Number: 2019955378 British Library Cataloguing-in-Publication Data A CIP record for this book is available from the British Library ISBN 978-1-78945-001-9 ERC code: PE1 Mathematics PE1_21 Application of mathematics in industry and society
4 Preface
5 1 Discrete Time Single-server Queues with Interdependent Interarrival and Service Times 1 Discrete Time Single-server Queues with Interdependent Interarrival and Service Times Attahiru Sule ALFA University of Manitoba, Canada and University of Pretoria, South Africa Discrete time single-server queues in which the interarrival and service times are interdependent are presented. First, we study the simple Geo/Geo/1 system, let the interarrival times depend on the service times and then consider special cases. The idea is then extended to the PH/PH/1 system. We then consider the case where the interarrival times are constructed from a combination of a set of interarrival times driven by the service times distribution. The initiating vector for the resulting combined PH distribution for the interarrival times is constructed as a function of the service times distribution, so that any changes in the service time distributions are reflected in this initiating vector. We capitalize on the structures of discrete phase type distributions in generalizing the resulting interarrival times. Finally, we introduce a general case where there is interdependence between service and interarrival times. We present a generalized matrix version of the bivariate geometric distribution, which can be used to capture some interdependence between the interarrival and service times.
1.1. Introduction 1.2. The Geo/Geo/1 case 1.3. The PH/PH/1 case 1.4. The model with multiple interarrival time distributions 1.5. Interdependent interarrival and service times 1.6. Conclusion 1.7. Acknowledgements 1.8. References
6 2 Busy Period, Congestion Analysis and Loss Probability in Fluid Queues 2.1. Introduction 2.2. Modeling a link under congestion and buffer fluctuations 2.3. Fluid queue with finite buffer 2.4. Conclusion 2.5. References
7 3 Diffusion Approximation of Queueing Systems and Networks 3.1. Introduction 3.2. Markov queueing processes 3.3. Average and diffusion approximation 3.4. Markov queueing systems 3.5. Markov queueing networks 3.6. Semi–Markov queueing systems 3.7. Acknowledgements 3.8. References
8 4 First-come First-served Retrial Queueing System by Laszlo Lakatos and its Modifications 4.1. Introduction 4.2. A contribution by Laszlo Lakatos and his disciples 4.3. A contribution by E.V. Koba 4.4. An Erlangian and hyper-Erlangian approximation for a Laszlo Lakatos-type queueing system 4.5. Two models with a combined queueing discipline 4.6. References
9 5 Parameter Mixing in Infinite-server Queues 5.1. Introduction 5.2. The M Λ/Cox n/∞ queue 5.3. Mixing in Markov-modulated infinite-server queues 5.4. Discussion and future work 5.5. References
10 6 Application of Fast Simulation Methods of Queueing Theory for Solving Some High-dimension Combinatorial Problems 6.1. Introduction 6.2. Upper and lower bounds for the number of some k -dimensional subspaces of a given weight over a finite field 6.3. Evaluation of the number of “good” permutations by fast simulation on the SCIT-4 multiprocessor computer complex 6.4. References
11 7 Diffusion and Gaussian Limits for Multichannel Queueing Networks 7.1. Introduction 7.2. Model description and notation 7.3. Local approach to prove limit theorems 7.4. Limit theorems for networks with controlled input flow 7.5. Gaussian approximation of networks with input flow of general structure 7.6. Limit processes for network with time-dependent input flow 7.7. Conclusion 7.8. Acknowledgements 7.9. References
12 8 Recent Results in Finite-source Retrial Queues with Collisions 8.1. Introduction 8.2. Model description and notations 8.3. Systems with a reliable server 8.4. Systems with an unreliable server 8.5. Conclusion 8.6. Acknowledgments 8.7. References
13 9 Strong Stability of Queueing Systems and Networks: a Survey and Perspectives 9.1. Introduction 9.2. Preliminary and notations 9.3. Strong stability of queueing systems 9.4. Conclusion and further directions 9.5. References
14 10 Time-varying Queues: a Two-time-scale Approach 10.1. Introduction 10.2. Time-varying queues 10.3. Main results 10.4. Concluding remarks 10.5. References
15 List of Authors
16 Index
17 End User License Agreement
1 Chapter 2 Figure 2.1. A classical busy period Figure 2.2.A period under level x Figure 2.3. A busy period with losses Figure 2.4. A period of level greater than z
2 Chapter 4 Figure 4.1.
3 Chapter 5 Figure 5.1.Cor(Λ( t ), X 1( t )) for μ 1= 1, γ = 2 and D Λ= 2. For a color version ... Figure 5.2. Estimated distribution of Xi for several phases i, with Λ ~ U (0, 6)... Figure 5.3. Histogram estimating the distribution of X, with Λ ~ U (0, 6) and γ =... Figure 5.4. Estimated distribution of X for different values of γ, with Λ ~ U (0,... Figure 5.5.Cor( X ,Λ) for DΛ = 1 and γ = 0.5. For a color version of this figure, s...
4 Chapter 6 Figure 6.1. A matrix determining the base vectors of some subspace
5 Chapter 8 Figure 8.1.Retrial queuing system of type M/GI/1//N with collisions of the cust... Figure 8.2.Density function of the gamma distribution. For a color version of t... Figure 8.3.Bimodal probability distribution of the number of customers in the s... Figure 8.4.Steady-state distributions. For a color version of this figure, see ... Figure 8.5. vs λ∕ N , 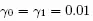 Figure 8.6. vs λ∕ N ,
Figure 8.6. vs λ∕ N , 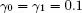 Figure 8.7.Reliable no conflict, reliable with conflict, and unreliable with co... Figure 8.8.Comparison of steady-state distributions. For a color version of thi...
Figure 8.7.Reliable no conflict, reliable with conflict, and unreliable with co... Figure 8.8.Comparison of steady-state distributions. For a color version of thi...
Читать дальше

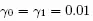 Figure 8.6. vs λ∕ N ,
Figure 8.6. vs λ∕ N , 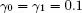 Figure 8.7.Reliable no conflict, reliable with conflict, and unreliable with co... Figure 8.8.Comparison of steady-state distributions. For a color version of thi...
Figure 8.7.Reliable no conflict, reliable with conflict, and unreliable with co... Figure 8.8.Comparison of steady-state distributions. For a color version of thi...










