Carlos Alberto Cardona - La pirámide visual - evolución de un instrumento conceptual

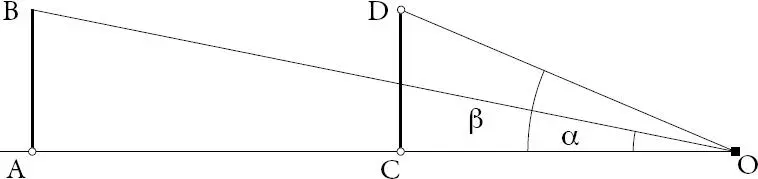
Figura 1.3. Teorema 3

Fuente : Elaboración del autor. La figura cuenta con modelación en el micrositio.

El comportamiento de la amplitud angular (trazo continuo) y de la tangente de dicha amplitud (trazo discontinuo) en relación con la distancia del objeto al observador puede apreciarse en la gráfica de la figura 1.4. 31La amplitud angular no es inversamente proporcional a la distancia (como sí lo es la tangente de dicha amplitud); salvo quizá, con cierto nivel de aproximación, para distancias grandes, para las cuales la amplitud angular es muy pequeña.

Erwin Panofsky ha llamado la atención acerca de la dificultad que introduce esta proposición en el marco de los esquemas conceptuales que orientan la perspectiva renacentista (1927/2003, pp. 19-20).

Teorema 4 (Proposiciones 10, 11, 13, 14) . Cuando el ojo se encuentra en un plano diferente a los objetos que divisa, ocurre que si el ojo está por encima, los objetos más alejados parecerán más elevados, y si está por debajo, dichos objetos parecerán más bajos.

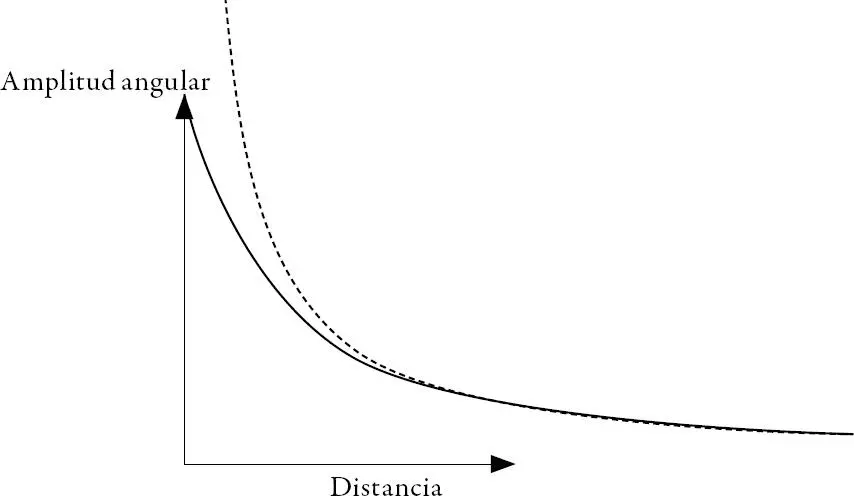
Figura 1.4. Comportamiento de la amplitud angular con la distancia

En trazo continuo se representa el comportamiento de la amplitud angular; en trazo discontinuo, el de la tangente de dicha amplitud.

Fuente : Elaboración del autor. La figura cuenta con modelación en el micrositio.

Supongamos que el observador O , desde un plano más elevado, contempla los puntos B , C , D sobre la misma recta, con D más alejado que B (véase figura 1.5). Al trazar los rayos visuales dirigidos a dichos puntos, el observador notará que cruzan la perpendicular a AD , trazada por Z , en el siguiente orden de abajo a arriba: B ′, C ′, D ′. En forma análoga, al contemplar E , F , G desde un punto más bajo, los objetos más alejados aparecerán más bajos.

El razonamiento es interesante, toda vez que la recta ZE ′ cumple el mismo papel que siglos más adelante desempeñará el velo de Alberti. 32También se puede advertir que el punto al que parece que convergen las paralelas AD y EG ha de encontrarse a la misma altura de O .

Teorema 5 (Proposiciones 22-27) . Cuando observamos una esfera, ella tiene la apariencia de un círculo en un plano perpendicular a la recta que une el ojo y el centro de la esfera. Además, el radio de tal círculo es menor que el radio aparente que le hubiese correspondido a la esfera completa.

Figura 1.5. Teorema 4

Fuente : Elaboración del autor. La figura cuenta con modelación en el micrositio.

Imaginemos el observador en el punto O y la esfera de centro A , cuyo corte con uno de los planos que contiene la recta AO produce la circunferencia de radio AB (véase figura 1.6). La circunferencia de diámetro AO en el plano mencionado corta a la esfera en los puntos B y D , que son precisamente los puntos en los que OB y OD son tangentes a la esfera en el plano que hemos acotado.

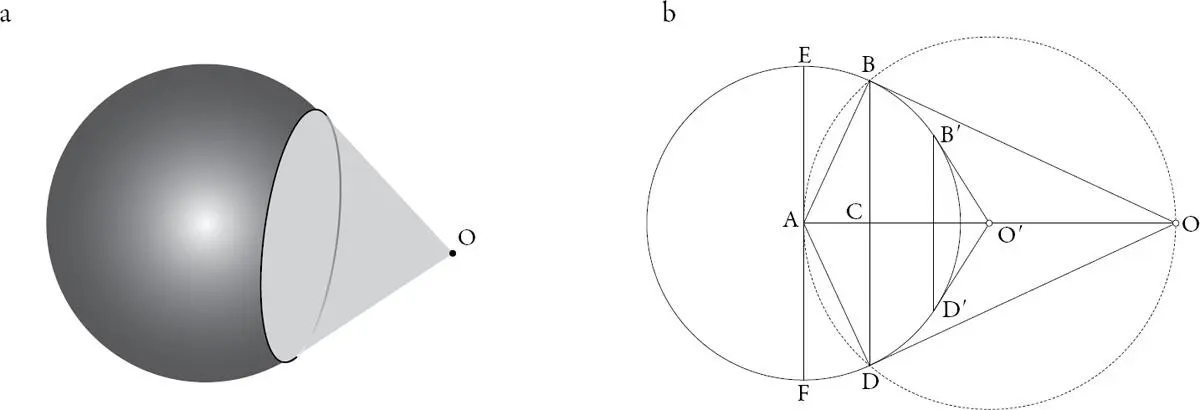
Figura 1.6. Teorema 5. a . Visión de una esfera; b . esfera reducida

Fuente : Elaboración del autor. Las figuras cuentan con modelación en el micrositio.

Si hacemos girar BC en torno al eje AO , surge un círculo en un plano perpendicular a AO . Este círculo determina la parte visible de la esfera para un observador en O . Ninguno de los puntos de la esfera entre B y E o D y F podrá ser visto, pues allí no incide ningún rayo que no sea oculto por el cono OBD (postulado 3).

Por otra parte, dado que BD es menor que EF , el diámetro del círculo aparente resulta menor que el diámetro de la esfera.

La proposición 22 sugiere que los puntos de la esfera entre B y D dan la apariencia de un segmento de recta en el plano perpendicular a AO . La argumentación es correcta si asumimos que la esfera está tan alejada que perdemos de vista la convexidad o no podemos apreciar matices singulares, como sombras o texturas en la superficie. Este teorema singular explica por qué el Sol y los planetas, pese a su esfericidad, se observan como discos circulares de diámetros menores que los que corresponderían a las semiesferas completas. 33

Si O se acerca a la esfera, la diferencia de tamaños entre BD y EF es más acentuada (proposición 24). Si O ′ es el nuevo punto de observación, la esfera se contemplará bajo el aspecto del círculo de diámetro B ′ D ′, es decir, una porción más reducida de la semiesfera que la marcada por BD . Sin embargo, tendremos la ilusión de estar contemplando más, toda vez que el ángulo D ′ O ′ B ′ es mayor que el ángulo BOD .

Teorema 6 (Proposiciones 34-36) . La apariencia que una circunferencia da a un observador que la mira desde otro plano, depende de la ubicación de este. Si él se encuentra en un punto sobre la recta que, a partir del centro, es perpendicular al plano de la circunferencia, contemplará todos los diámetros bajo la misma amplitud angular; en consecuencia, el rasgo de circularidad se conserva.

Si el observador, en un plano diferente al de la circunferencia, se halla a una distancia del centro igual al radio de la misma, desde allí también se apreciarán todos los diámetros bajo la misma apariencia y, en consecuencia, el rasgo de circularidad así mismo se conservará.

Si OA es perpendicular al plano BECD (véase figura 1.7), no hay dificultad en advertir que el ángulo BOC es igual al ángulo DOE , y así para cualquier otro diámetro diferente. Entonces, un observador en O divisará todos los diámetros bajo la misma amplitud angular y por ello parecerán iguales (postulado 4).

Si OA no es perpendicular al plano, pero su longitud es igual a la de AB , el ángulo BOC será recto, sin importar el diámetro al cual hagamos referencia. En las posiciones restantes, los diámetros tendrán apariencias disímiles.

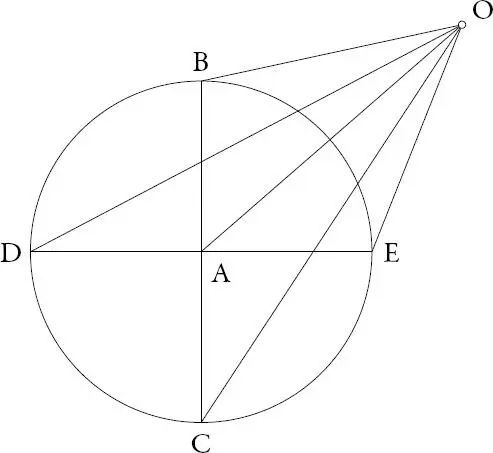
Figura 1.7. Teorema 6

Fuente : Elaboración del autor. La figura cuenta con modelación en el micrositio.

Hemos presentado un conjunto de ejemplos que muestran cómo se puede valorar la óptica de Euclides, como un canon que propone un lenguaje e instrumentos de control matemático para ofrecer explicaciones de fenómenos simples que estamos dispuestos a reunir bajo un inventario de situaciones familiares: 1) los objetos que se alejan disminuyen su apariencia en el campo visual; 2) cuando un observador se ubica entre segmentos paralelos de gran longitud, pero en un plano diferente, los observará como si tales segmentos se reunieran en un punto que se encuentra a la misma altura del observador; y 3) no es posible ver, en forma simultánea, todos los puntos de una esfera.