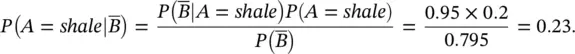In the Bayesian setting, the prior probability represents the prior knowledge about the event of interest and the likelihood function is the probabilistic formulation of the relation between the event of interest and the observable event (i.e. the data). The intuitive idea of Bayes' theorem is to reduce the uncertainty in the prior probability by integrating additional information from the data.
For example, in reservoir modeling applications, the event A might represent the occurrence of porous rocks with porosity higher than 0.30 and the event B might represent the measurements of seismic velocity. Typically, in geoscience studies, prior information about rock and fluid properties can be obtained from geological models, analogues, outcrops, or nearby fields, whereas the likelihood function can be calculated using geophysical models or estimated from available datasets. In the porosity–velocity example, the prior probability of the occurrence of high‐porosity rocks in a given reservoir can be estimated from core samples or data from nearby fields, whereas the likelihood function can be computed using a rock physics model that predicts the velocity response in porous rocks ( Chapter 2).
The calculation of the normalizing constant P ( B ) in Bayes' theorem ( Eq. 1.8) often requires additional probability tools. A useful result in probability theory is the theorem of total probability. We consider an event A and an ensemble of n events { E i} i=1,…,n, and we assume that the events { E i} are mutually exclusive ( E i∩ E j= ∅, for all i , j = 1, …, n with i ≠ j ) and collectively exhaustive ( 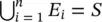 ). These assumptions mean that every possible outcome of the event A is an outcome of one and only one of the events { E i} i=1,…,n. Then, the probability P ( A ) of the event A is given by:
). These assumptions mean that every possible outcome of the event A is an outcome of one and only one of the events { E i} i=1,…,n. Then, the probability P ( A ) of the event A is given by:
(1.9) 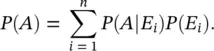
The theorem of total probability ( Eq. 1.9) expresses the probability of an outcome of an event that can be realized via several distinct events as the contribution of the conditional and marginal probabilities.
We illustrate the application of Bayes' theorem and the theorem of total probability with an example related to the classification of porous rocks. A team of reservoir geologists classifies a group of porous rocks in a reservoir in three categories: shale, silt, and sand. The geologists are interested in rock samples with porosity greater than 0.20. The team wants to answer the following questions: (i) What is the probability of a rock having porosity greater than 0.20? (ii) If a core sample has porosity greater than 0.20, what is the probability that the rock sample is a sand? (iii) If a core sample has porosity less than or equal to 0.20, what is the probability that the rock sample is a shale?
Based on a nearby field, it is estimated that 20% of the reservoir rocks are shale, 50% are silt, and 30% are sand. If the event A represents the rock type occurrence, the available information can be written in terms of the prior probability P ( A ) of the event A as:
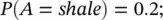
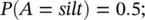
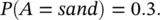
The literature data for the geological environment under study indicate that the probability of observing porosity greater than 0.20 in that specific region is 0.05 in shale, 0.15 in silt, and 0.4 in sand. This information represents the likelihood function. If the event B represents the occurrence of rock samples having porosity greater than 0.20, then the available information can be written in terms of the conditional probability P ( B ∣ A ):
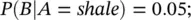
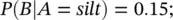
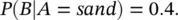
We first compute the probability P ( B ) of observing high porosity in a rock sample, using the theorem of total probability ( Eq. 1.9):
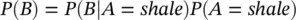
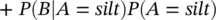
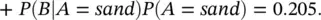
Then, we compute the posterior probability P ( A = sand ∣ B ) of a sample with porosity greater than 0.20 being a sand using Bayes' theorem ( Eq. 1.8):
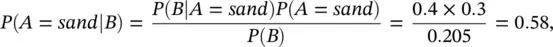
where the normalizing constant P ( B ) is computed using the theorem of total probability, as shown in question (i).
Finally, the probability 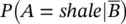 of a sample with porosity less than or equal to 0.20 (event
of a sample with porosity less than or equal to 0.20 (event 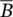 ) being a shale can be computed in two steps. First, we compute the marginal probability of the complementary event
) being a shale can be computed in two steps. First, we compute the marginal probability of the complementary event 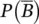 as:
as:
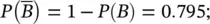
then we compute the conditional probability 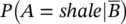 using Bayes' theorem ( Eq. 1.8):
using Bayes' theorem ( Eq. 1.8):
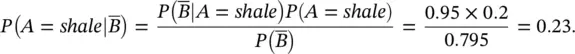
We now consider a variable X , whose value is uncertain. In statistics, such a variable is called a random variable, or a stochastic variable. A random variable is a variable whose value is subject to variations and cannot be deterministically assessed. In other words, the specific value cannot be predicted with certainty before an experiment. Random variables can take discrete or continuous values. In geophysics, a number of subsurface properties, such as facies types, porosity, or P‐wave velocity, are considered random variables, because they cannot be exactly measured. Direct measurements are also uncertain, and the measurements should be treated as random variables with a distribution that captures the measurement uncertainty.
Читать дальше

 ). These assumptions mean that every possible outcome of the event A is an outcome of one and only one of the events { E i} i=1,…,n. Then, the probability P ( A ) of the event A is given by:
). These assumptions mean that every possible outcome of the event A is an outcome of one and only one of the events { E i} i=1,…,n. Then, the probability P ( A ) of the event A is given by: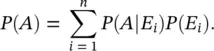
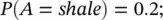
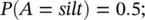
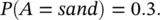
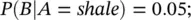
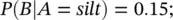
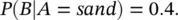
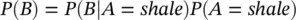
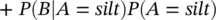
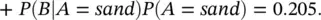
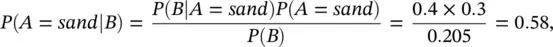
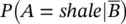 of a sample with porosity less than or equal to 0.20 (event
of a sample with porosity less than or equal to 0.20 (event 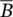 ) being a shale can be computed in two steps. First, we compute the marginal probability of the complementary event
) being a shale can be computed in two steps. First, we compute the marginal probability of the complementary event 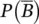 as:
as: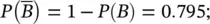
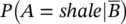 using Bayes' theorem ( Eq. 1.8):
using Bayes' theorem ( Eq. 1.8):