Luis Darío Salamone - Topología del amor

¿Qué nos muestra esta regla de Euler? Además de solucionar el problema de los puentes, que a los parroquianos entre una cerveza y otra se les complicaba resolver, nos permite plantearnos la existencia de propiedades fundamentales de las figuras geométricas que no dependen del tamaño o la forma. Si a cualquiera de estas figuras la deformamos no afectamos el estudio de esas propiedades.

Maurice Fréchet y Ky Fan en Introducción a la topología combinatoria ,(8) plantean ciertas distinciones realizadas por Henri Poncairé, que nos habla de tres clases de geometrías:

1. La geometría métrica: se encuentra fundada en la noción de distancia. Dos figuras resultarán equivalentes cuando son iguales, hay que entender esta igualdad en el sentido matemático del término.

2. La geometría proyectiva: está fundada en la noción de línea recta. Para que dos figuras sean equivalentes, no necesariamente tienen que ser iguales, basta con pasar de una a otra por medio de una transformación proyectiva. Es decir, que una sea la perspectiva de otra. Se la puede llamar Geometría Cualitativa. Si bien, en apariencia, la cantidad desempeña un papel menos importante, esto no es tan así. Se utilizan, por ejemplo, reglas, las cuales son instrumentos de medida.

3. La tercera geometría sería la que nos interesa: la topología , donde la cuestión de la cantidad está suprimida por completo, es decir, que se trata de una disciplina puramente cualitativa. Dos figuras serán equivalentes, siempre que pasemos de una a otra por medio de una “deformación continua”. No importa qué tipo de deformación sea, con tal de que sea respetada la continuidad. Un círculo, una elipse, una curva cerrada cualquiera, son equivalentes.

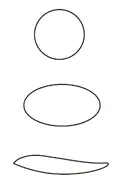
CÍRCULO, ELIPSE Y FIGURA CERRADA

Pero todas estas figuras no son equivalentes a un segmento de recta, ya que éste no es cerrado.

Tomemos un ejemplo que nos resulte claro. Imaginemos un modelo y la copia de ese modelo realizado por un dibujante para nada habilidoso, al cual le tiemblan las manos, altera todas las proporciones y el temblor se manifestará en curvas que en verdad no se encuentran en el modelo.

Desde la geometría métrica o desde la proyectiva no habrá equivalencia entre las figuras, sin embargo, serán equivalentes desde el punto de vista de la topología.

Hay que tener en cuenta que no importa si nuestro pésimo dibujante altera las proporciones, incluso groseramente, si en lugar de líneas rectas aparecen por ejemplo zig zags o cosas por el estilo, pero para que se conserven las propiedades topológicas no se puede dibujar una línea curva en lugar de una línea abierta, o líneas que se corten en un punto, una superficie con abertura en lugar de una que no la tiene, etc.

MODELO Y COPIA

Para Fréchet y Fan en la topología es dónde interesa verdaderamente la “intuición geométrica”. Le interesa el espacio y se distingue de las geometrías métricas de Euclides, de

Lobchensky, de Reimann, que tratan sobre magnitudes y ángulos. Se trata entonces directamente de una Geometría no cuantitativa .

En este campo no nos vamos a preguntar “¿qué longitud?”, “¿a qué distancia?”, “¿de qué magnitud?”, sino más bien que nos haremos preguntas tales como “¿dónde?”, “¿entre qué?”, “¿interior o exterior?”.

El término Analysis Situs se lo debemos a Leibniz (1679). Si bien el invento, como hemos visto, fue de Euler, el primer Estudio sobre topología que se conoce es de 1847 y pertenece a Johann Benedict Listing, que fue el primero en hablar de topología. Listing va a descubrir las propiedades de la Banda de Moebius incluso antes que el señor que finalmente se quedará con el nombre de la banda. En verdad la descubrieron cada uno de forma independiente en 1958.

Se define a la topología como “El estudio de las propiedades de los espacios, o sus configuraciones, invariantes bajo transformaciones continuas uno-a-uno”.

“Invariantes” es un término inventado por el inglés Sylvester, a quien se lo llamó el “Matemático Adán”, porque introdujo muchos nombres a las matemáticas.

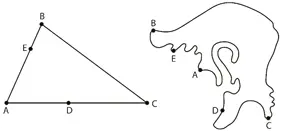
La topología estudia entonces la posición y la relación de las partes de una figura con respecto a otra, sin tener en cuenta la forma y el tamaño.

Vamos a dibujar un triángulo plano. Topológicamente sería equivalente a la figura de al lado, un poco surrealista, que como ven pueden localizar los mismos puntos. Cambiaron las líneas rectas por curvas, los ángulos se deformaron, tanto como las longitudes. Sin embargo, hay propiedades que no están afectadas: a estas se las llaman “invariantes”. El orden de los puntos no cambia, es invariante. La topología hace de estas invariantes un sistema matemático.

Si tomamos dos anillos de hierro unidos como aparecen en la figura que sigue, no podremos separarlos a menos que se rompa uno de ellos. Esto resulta evidente, pero sin la topología no podríamos demostrarlo matemáticamente. Porque la topología se ocupa de estudiar si las propiedades espaciales cambian o no.

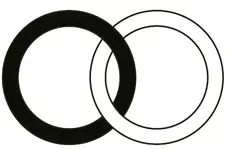
ANILLOS ENCADENADOS

Vamos a realizar una prueba que podríamos considerar topológicamente equivalente. Seguimos el libro de Kasner & Newman que conocí gracias a Jorge Luis Borges y he recomendado tantas veces; quizás se trate de un libro de difusión, pero les permitirá a quienes se han alejado de las matemáticas por considerarlas aburridas, interesarse de una forma insospechada. Mi amigo Oscar Lamorgia me recordó recientemente que se lo había recomendado hace como 30 años. Y le pasó exactamente eso.

Atemos las dos muñecas de alguien con una cuerda. Y hagamos lo propio con otra cuerda en las dos muñecas de otra persona. Pero cruzando las sogas para que queden enlazados como nos muestra la siguiente figura.

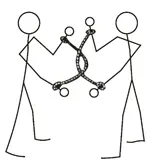
PAREJA ENCADENADA

Pueden probar con su pareja si les resulta posible separarse, sin romper la cuerda y sin sacarse las ataduras de las muñecas. Quizás no logren hacerlo, pero se van a divertir.

Aunque les anticipo que para mí esta es la demostración topológica de la inexistencia de la relación sexual. Esa inexistencia que suple el amor.

Van a poder comprobar la ilusión de estar atados al otro, creyendo que es para siempre. Pero eso de estar soldados, como le pasó al primitivo andrógino, tiene su límite. Por supuesto eso no implica que de vez en cuando podamos juntarnos para divertirnos un poco.

La pareja que parecía prisionera del amor, con algunos movimientos puede separarse, respetando las propiedades topológicas que traducimos en no soltar, no desatarse o no sacarse la soga de las muñecas. En la topología, como en el amor, las apariencias engañan.

1- Lacan, J., El Seminario, Libro 1, Los escritos técnicos de Freud , Paidós, Barcelona, 1986, p. 125.

2- Lacan, J., “El mito individual del neurótico”, en Intervenciones y textos 1 , Manantial, Buenos Aires, 1985.