Luis Darío Salamone - Topología del amor

Suele ocurrir que, sin que nos demos cuenta, nos manejemos en la vida de una manera topológica. Por ejemplo, alguien quiere dirigirse a un lugar, y supongamos que para eso necesita dirigirse a una estación de subterráneos; entonces me pregunta a qué distancia le queda dicha estación, puedo orientarlo diciéndole que camine mil metros, doble a la derecha en ángulo recto y camine otros trescientos metros.

Otra persona, desde una concepción topológica, no preguntaría por la distancia, sino que preguntaría directamente cómo puede llegar al lugar, y nosotros, estudiantes de la topología como somos, con determinados elementos, lo ayudaríamos a llegar a su destino sin hablarle en términos numéricos. Podríamos decirle, por ejemplo, que camine hasta el sauce llorón y luego doble a su derecha hasta un cartel grande que dice: “Quédate en casa”. Debajo del cartel puede encontrar la boca de subte. Tal vez esa persona ni imagine que, al ingresar al vagón y ver la línea con las estaciones que suelen estar arriba de la puerta, nuevamente se orientará topológicamente. Efectivamente, los planos de las líneas de subterráneos son un buen ejemplo de este tipo de representación donde no importan las medidas ni las formas. O sea que no interesan las cuestiones cuantitativas, sino cualitativas.

Como lo afirman Kasner & Newman: “Problemas aparentemente triviales han dado origen al desarrollo de varias teorías matemáticas”.(7) Así como la teoría de la probabilidad nació del cubilete de dados de los jóvenes nobles de Francia, la topología nació en las tabernas de Koenigsberg.

En el siglo XVIII, siete puentes atravesaban el río Pregel que fluía rodeando una pequeña ciudad universitaria llamada Koenigsberg y permitía la comunicación con una pequeña isla llamada Kneiphof. Se trata de una ciudad de Prusia Oriental, que luego sería parte de Alemania y más tarde se convertiría en Kaliningrado para formar parte de Rusia

A sus habitantes les gustaban, además de la cerveza, los paseos. Mientras tomaban en la taberna se preguntaban: ¿cómo puede alguien realizar un paseo el domingo a la tarde por esta zona, de tal modo que pase una sola vez por cada uno de los siete puentes, y regrese al punto de partida?

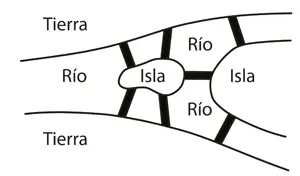
LOS PUENTES DEL RÍO PREGEL

Los habitantes del pueblo intentaron una y otra vez y llegaron a la conclusión de que no era posible realizarlo; pero esta convicción de imposibilidad necesitaba de una demostración matemática.

Los ecos de este problema le llegaron a Leonhard Euler, oriundo de aquellas tierras, que se encontraba en San

Petersburgo, desempeñándose como matemático en la Corte de Catalina la Grande. Con la nostalgia que sentía por su patria (como si a nosotros se nos hubiera ocurrido tararear un tango en Rusia) al matemático se le ocurrió resolver el problema. Presentó su resolución en la Academia Rusa de San Petersburgo en 1735. No solo eso, al demostrar que el viaje por los siete puentes sin volver a pasar por el mismo, era imposible; fundó la teoría de los grafos, y con ello nos acercó a la topología.

La operación de Euler consistió en simplificar, en realizar una abstracción del plano. Reemplazó la tierra por simples puntos y los puentes por líneas que los unían. De esta operación resultó un gráfico. La pregunta, a partir de entonces, consistió en saber si esta gráfica puede dibujarse con un trazo continuo sin levantar la punta del lápiz. Hacerlo sería equivalente a atravesar físicamente los puentes en una caminata.

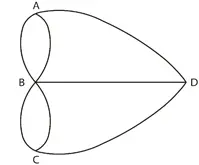
LA OPERACIÓN DE EULER

La topología nació con esta demostración matemática para la cual no se necesitan números. Alcanzaba para eso un gráfico. Se trata entonces de una geometría del lugar, de la posición, del espacio. Nos introduce en otra lógica que la euclidiana.

La pregunta, a partir de esto, consiste en saber si esta gráfica puede dibujarse con un trazo continuo, sin levantar la tiza del pizarrón o el lápiz de la hoja. Hacerlo sería equivalente a atravesar físicamente los puentes en una caminata.

Es decir que matemáticamente el problema se reduce a recorrer una gráfica. Tenemos un número finito de puntos llamados vértices y un número de arcos. Los extremos de los arcos son los vértices. Dos arcos no tienen un punto en común, a excepción de un vértice. De acuerdo a la cantidad de arcos que concurran en un vértice, este será par o impar.

Lo que Euler descubrió es que solo puede recorrerse una gráfica pasando por sus arcos una sola vez, comenzando y terminando por el mismo punto, si tenemos en la gráfica vértices pares.

Nuestra figura tiene cuatro vértices impares, por lo tanto, no alcanzará con un solo viaje para recorrerla, harán falta dos.

Ahora, si dibujamos un arco adicional entre A y C, y se retira el arco que va entre B y D, todos los vértices serán pares, por lo tanto, la gráfica podrá ser recorrida en un solo viaje.

Si no retiramos BD podemos cruzar todos los puentes una sola vez, pero sin terminar donde empezamos. El paseo deberá iniciarse desde un vértice impar.

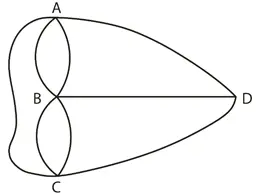
GRAFO CON PUENTE AGREGADO

Si la gráfica tiene como máximo dos vértices impares, puede ser igualmente recorrida, pero sin volver al punto de partida. Es más, generalmente si la gráfica contiene una determinada cantidad de impares, esa será la cantidad de viajes necesarios para recorrerla.

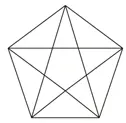
Este tipo de problemas datan de la más remota antigüedad. Kasner & Newman rescatan una figura que tiene su lugar en la historia de la magia y la superstición, conocida por los mahometanos y los hindúes, por pitagóricos y cabalistas. Era utilizada como talismán, se la grababa en la cuna de los niños para ahuyentar el mal, o en los establos. El cristianismo lo utilizó para representar las cinco llagas de Cristo. Es una estrella pentagonal que algunos hemos dibujado y podemos recorrer en un solo trazo. También llamada pentagrama, pentáculo o estrella pitagórica. También pentalfa, ya que se dibujan cinco letras A o alfa.

ESTRELLA PITAGÓRICA

Incluso, siguiendo la teoría de Euler, una figura en apariencia más complicada como la que dibujamos a continuación, puede ser recorrida en un solo trazo. Se trata de un pentagrama en el interior de un pentágono. Un nudo simple atado a una cinta de papel estirado y aplanado termina formando un pentágono perfecto. También podemos encontrar en estos diagramas la sección aurea, una de las tres proporciones simples que se encuentran en los primeros polígonos.

ESTRELLA EN PENTÁGONO

En cambio, esta otra figura, en apariencia más simple, no puede ser recorrida sin tener que levantar la tiza o el lápiz para dibujarla.

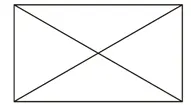
CRUZ EN RECTÁNGULO