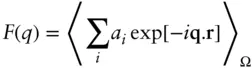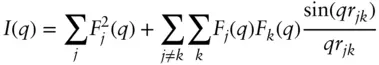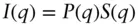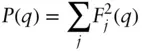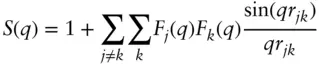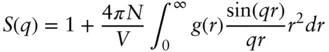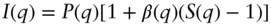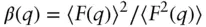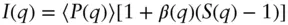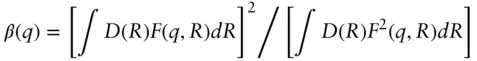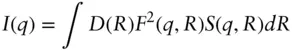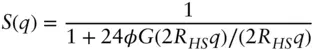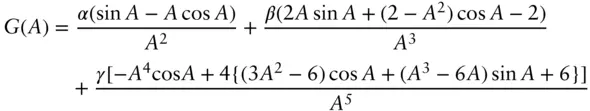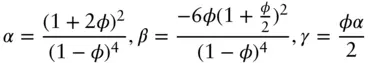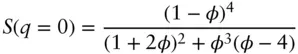Ian W. Hamley - Small-Angle Scattering

where F ( q ) is the amplitude of scattering from within a particle:

( 1.27)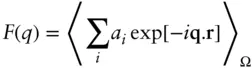

which is analogous to an isotropic average over Eq. (1.2).

Equation (1.25)can be separated into intra‐ and inter‐ particle components:

(1.28)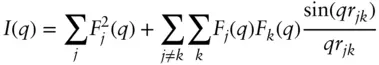

This can be written for the monodisperse ensemble of spherically symmetric particles as

(1.29)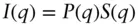

Here the form factor is

(1.30)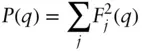

and the structure factor is

(1.31)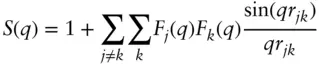

In a sufficiently dilute system only the form factor needs to be considered. Intermolecular interferences are manifested by the increasing contribution of the structure factor as concentration is increased. In many micellar, biomolecular, and surfactant systems in dilute aqueous solution, structure factor effects may not be observed (over the typical q range accessed in most SAXS measurements). At high concentration, the structure factor is characterized by a series of peaks (due to successive nearest neighbour correlations, next nearest neighbour correlations etc.) the intensity decaying as q increases, oscillating around the average value S ( q ) = 1. The structure factor is related by a Fourier transform to the radial distribution function g ( r ):

( 1.32)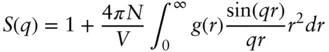

where V is the volume of the particle.

Figure 1.5shows the calculated total intensity within the monodisperse approximation (product of form and structure factors) for spheres of radius R = 30 Å (also hard sphere structure factor radius R H= 30 Å) at two volume fractions showing the increase in the contribution from the structure factor at low q including the development of a peak at q ≈ 0.1 Å −1.

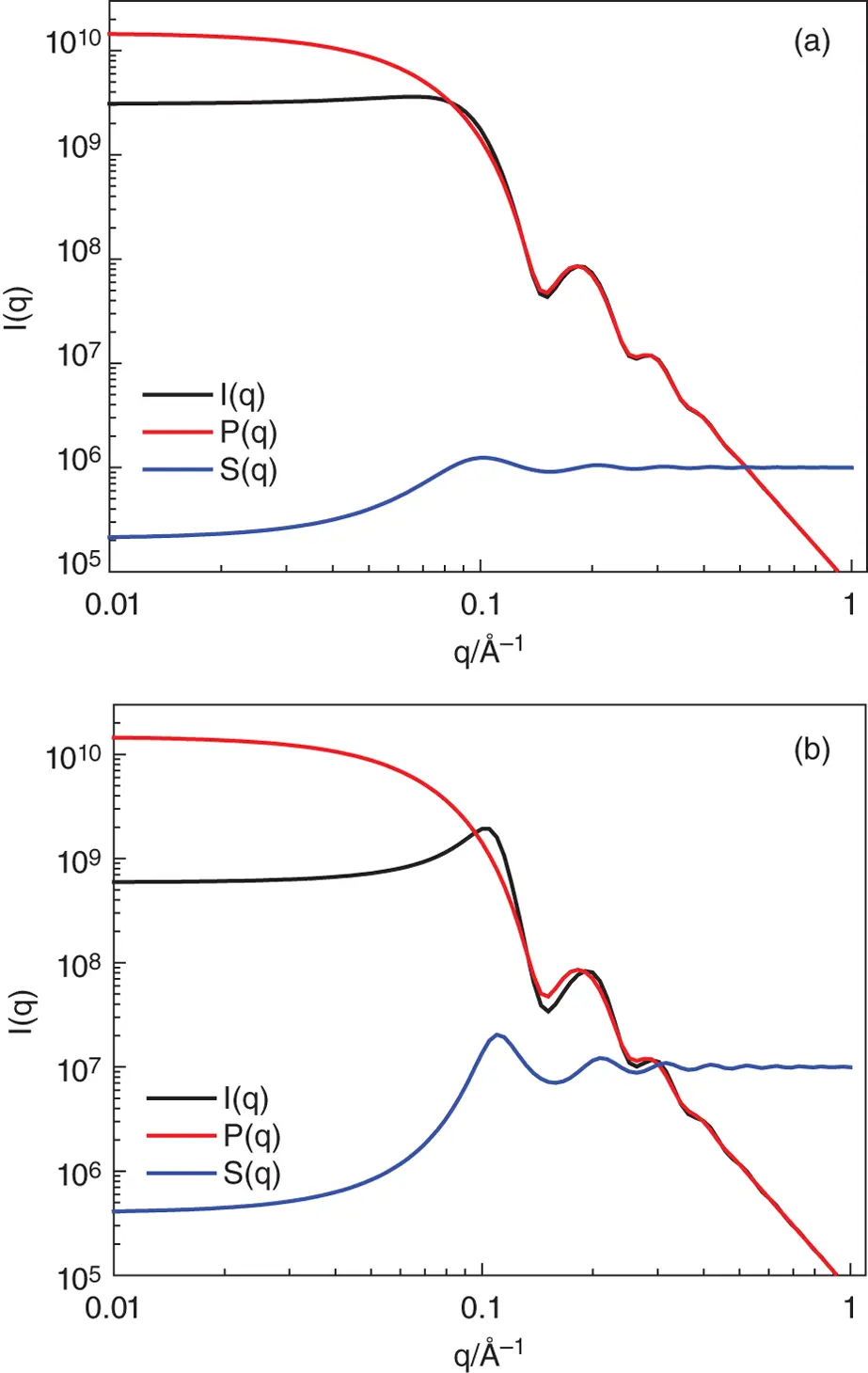
Figure 1.5 Calculated total intensity I ( q ) = P ( q ) S ( q ) in the monodisperse approximation for spheres with radius R = 30 Å (polydispersity σ = 3 Å, see Figure 1.19) and hard sphere structure factor with R HS= 30 Å and volume fraction (a) 0.2, (b) 0.4. The structure factor S ( q ) has been scaled by a factor of 10 5in (a) and 10 6in (b) for ease of visualisation.

The preceding derivation ( Eqs. (1.26)– (1.32)) applies for the case of monodisperse particles with spherical symmetry. Other expressions have been introduced for other cases. For particles that are slightly anisotropic, the ‘decoupling’ approximation [16] is often used. The intensity for monodisperse particles is written as

(1.33)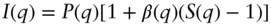

where

( 1.34)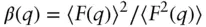

Here, F ( q ) is the ‘amplitude’ form factor, given by Eq. (1.27). Note that there is confusion in the literature, and the term structure factor can be used to refer to intensity or amplitude according to the context. Here, S ( q ) is used for intensity structure factor and F ( q ) for form amplitude factor. In Eq. (1.34), the structure factor is calculated for the average particle size defined as R av= [3 V /(4π)] 1/3[17].

For systems with small polydispersities, a decoupling approximation can also be used [17] according to the expression:

(1.35)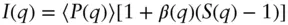

where

(1.36)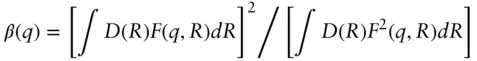

Here, D ( R ) is the dispersity distribution function ( Section 1.7.4), which may have a Gaussian or log‐normal function form, for example. The structure factor S ( q ) is evaluated for the average particle size.

An alternative approximation is the local monodisperse approximation, which treats the system as an ensemble of locally monodisperse components (i.e. a particle of a given size is surrounded by particles of the same size). The intensity is then [17]

(1.37)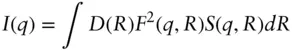

Other approximations for the factoring of form and structure factors have been proposed [17].

Analytical expressions for structure factors are available for a few simple systems including spherical and cylindrical particles [17, 18] and lamellar structures. For spheres, the hard sphere structure factor is the simplest model, as the name suggests this structure factor is derived based on purely steric interactions between solid packed spheres (volume fraction ϕ and hard sphere radius RHS ). It is written

( 1.38)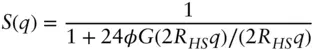

Here

(1.39)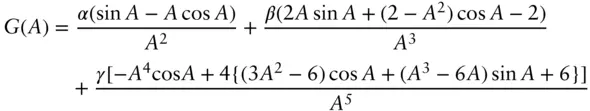

with

(1.40)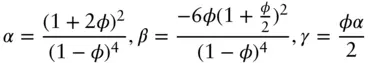

At q = 0, the Carnahan‐Starling closure to the hard sphere structure factor gives the expression [11, 19]

(1.41)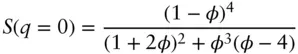

The sticky hard sphere potential allows for a simple attractive potential between spheres (the equation for the structure factor is presented elsewhere [17, 18]). For charged spherical particles, the screened Coulomb potential may be employed.

For cylinders, a random phase approximation (RPA, Section 1.8) equation may be used or the PRISM (polymer reference interaction site model, Section 5.8) structure factor. The RPA expression is