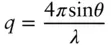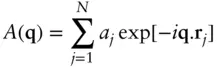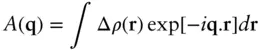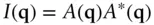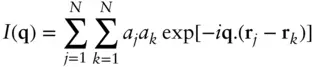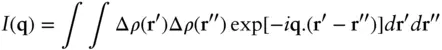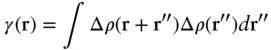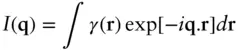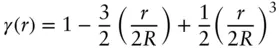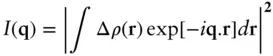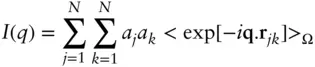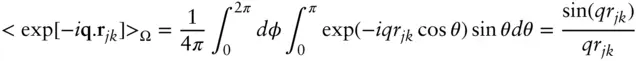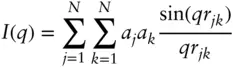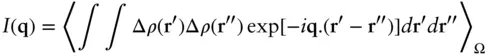1.2 WAVENUMBER AND SCATTERING AMPLITUDE
In a SAS experiment, the intensity of scattered radiation (x‐rays or neutrons) is measured as a function of angle and is presented in terms of wavenumber q . This removes the dependence on wavelength λ which would change the scale in a plot against angle, i.e. SAS data taken at different wavelengths will superpose when plotted against q , this is useful for example on beamlines where data is measured at different wavelengths (this is more common with neutron beamlines). The wavenumber quantity is sometimes denoted Q although in this book q is used consistently. The difference between incident and diffracted wavevectors q= k s− k iand since 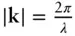 , and the scattering angle is defined as 2 θ ( Figure 1.1), the magnitude of the wavevector is given by
, and the scattering angle is defined as 2 θ ( Figure 1.1), the magnitude of the wavevector is given by
(1.1) 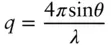
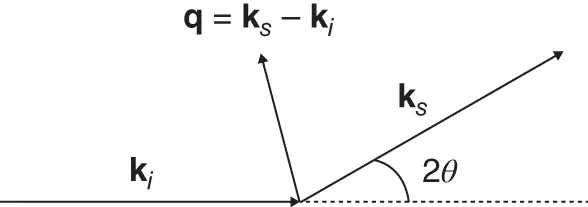
Figure 1.1 Definition of wavevector qand scattering angle 2 θ , related to the wavevectors of incident and scattered waves, k iand k f.
In some older texts, related quantities denoted s or S are used (these can correspond to q /2 or q /2π; the definition should be checked). The wavenumber q has SI units of nm −1, although Å −1is commonly employed.
The amplitude of a plane wave scattered by an ensemble of N particles is given by
( 1.2) 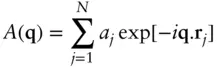
Here, the scattering factors aj are either the ( q ‐dependent) atomic scattering factors f j( q ) ( Section 4.4) for SAXS or the q ‐independent neutron scattering lengths bj for SANS ( Section 5.4).
For a continuous distribution of scattering density, Eq. (1.2)becomes
(1.3) 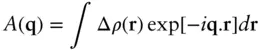
Here Δ ρ ( r) is the excess scattering density above that of the background (usually solvent) scattering, which is a relative electron density in the case of SAXS or a neutron scattering length density (Eq. (5.11)) in the case of SANS.
1.3 INTENSITY FOR ANISOTROPIC AND ISOTROPIC SYSTEMS AND RELATIONSHIPS TO PAIR DISTANCE DISTRIBUTION AND AUTOCORRELATION FUNCTIONS
1.3.1 General (Anisotropic) Scattering
In the following, notation to indicate that the intensity is ensemble or time‐averaged is not included for convenience (if the system is ergodic, which is often the case apart from certain gels and glasses etc., these two averages are equivalent).
The intensity is defined as
(1.4) 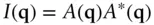
Thus, using Eq. (1.2), for an ensemble of discrete scattering centres
( 1.5) 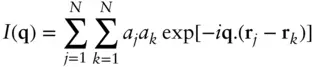
Whereas, for a continuous distribution of scattering density,
( 1.6) 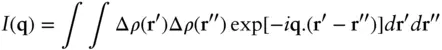
Equation (1.6)can also be rewritten in terms of an autocorrelation function (sometimes known as convolution square function) writing r′ − r″ = r
(1.7) 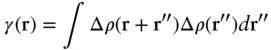
Then
( 1.8) 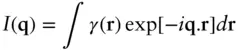
The autocorrelation function has the physical meaning of the overlap between a particle and its ‘ghost particle’ displaced by r( Figure 1.2). This function is the continuous version of the Patterson function familiar from crystallography.
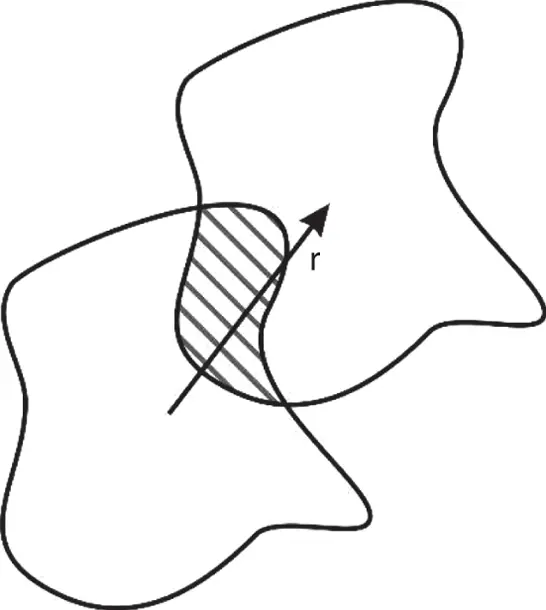
Figure 1.2 Ghost particle construction. The overlap volume (shaded) is the autocorrelation function.
The autocorrelation function for solid geometrical bodies can be calculated analytically. For a sphere of radius R the expression is isotropic and is given by [5–7]
(1.9) 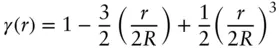
This is a smoothly decaying function of r . The expression for a cylinder is provided in Ref. [8] and can be calculated for other structures, asymptotic expressions for cylinders and discs are given in Eqs. (1.83)and (1.84).
Equation (1.6)can alternatively be written for uncorrelated scatterers as
( 1.10) 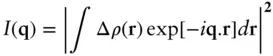
1.3.2 Isotropic Scattering Systems
For isotropic scattering the scattered intensity will only be a function of the wavenumber q and an orientational average (indicated by <..> Ω) is performed, i.e. Eq. (1.5)becomes
(1.11) 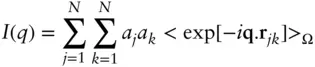
where r jk= r j− r k.
The average over all orientations of r jkcan be evaluated as follows
( 1.12) 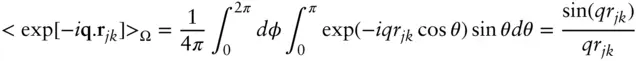
This leads to the Debye equation for scattering from an isotropically averaged ensemble:
(1.13) 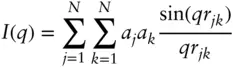
Considering a continuous distribution of scattering density, the orientational averaging of Eq. (1.12)has to be performed over Δ ρ ( r) since it is a function of r:
( 1.14) 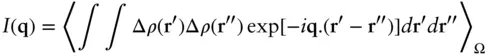
Читать дальше

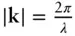 , and the scattering angle is defined as 2 θ ( Figure 1.1), the magnitude of the wavevector is given by
, and the scattering angle is defined as 2 θ ( Figure 1.1), the magnitude of the wavevector is given by