Chapter 5presents the theory of linear piezoelectricity, starting with some one dimensional examples in Section 5.1. Section 5.2 gives the detailed account of how the equations of linear piezoelectricity are derived from Maxwell's equations, and Section 5.2.2 summarizes the initial‐boundary value problem of linear piezoelectricity. Section 5.3 surveys the role of thermodynamics in the construction of various equivalent constitutive laws and their associated thermodynamic invariants. The structure of the constitutive laws generated by crystalline materials having different symmetry operations is described in Section 5.4.
Chapter 6focuses on the use of Newton's method to derive the governing equations for linearly piezoelectric composite structures. The axial actuator model, which is a prototype for the linear actuators of the type depicted in Figure 1.8, is treated in Sections 6.1 and 6.2. Section 6.3 presents an analysis of the beam actuator as shown in the introduction in Figure 1.9. Section 6.4 uses Newton's method to derive the governing equations for a simplified model of piezoelectric composite plate bending.
Chapter 7introduces powerful variational methods for deriving the governing equations of piezoelectric structures. The chapter begins with a review of variational calculus in Chapter 7.1. Hamilton's principle for mechanical systems is introduced in Section 7.2, and its generalization for linear piezoelectricity is presented in Section 7.3. The strength of these variational techniques is illustrated in Section 7.4, which shows how variational methods for electromechanical systems that consist of piezoelectric structures and attached ideal circuits can be modeled. Various authors have discussed variational methods for electromechanical systems over the years, and Section 7.5 discusses the relationships among some alternative forms of these principles. Section 7.6 illustrates how the electromechanical variational principle can be applied using Lagrangian densities 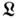 instead of Lagrangian functions
instead of Lagrangian functions 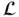 .
.
Chapter 8, the final chapter of this book gives a detailed description of approximation methods for linearly piezoelectric composite structures. The chapter begins in Section 8.1 with a discussion of the differences between classical, strong, and weak forms of the governing equations. As discussed in Section 8.1, the approximation strategies in the text are derived from the weak form of the governing equations. Section 8.2 gives a quick overview of modeling damping and dissipation, with the primary emphasis on viscous damping that is so popular in engineering vibrations texts. Galerkin approximations are introduced in Section 8.3, and example applications for the linear and bending actuators are summarized. Two classes of bases are described for use in the Galerkin approximations. Modal or eigenfunction bases are used in Section 8.3.1, and finite element functions are employed in Section 8.3.2. The chapter finishes with a collection of examples that summarize how transient and steady state solutions are obtained from the Galerkin approximations. Particular emphasis is placed on the derivation of complex frequency response equations and FRFs for the piezoelectric composite structures.
The Appendix contains three sections that provide supplementary material for the discussions throughout the text. Section S.1 gives a streamlined summary of the basic background for vibrations theory for single degree of freedom (SDOF) systems, distributed parameter systems (DPS), and multi‐DOF (MDOF) systems. A supplementary account of tensor analysis is given in Section S.2. For those students seeking to understand the simplified version of tensor analysis covered in Chapter 2, this section shows how the simplified account fits in the general theory. Finally, Section S.3 discusses details regarding distributional and weak derivatives beyond the brief account in Chapter 8. A rigorous definition of a weak derivative is given, and the Sobolev spaces 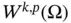 of all functions whose weak derivatives of order less than or equal to
of all functions whose weak derivatives of order less than or equal to 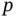 are elements of the Lebesgue space
are elements of the Lebesgue space 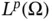 is defined.
is defined.
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.

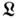 instead of Lagrangian functions
instead of Lagrangian functions 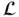 .
.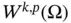 of all functions whose weak derivatives of order less than or equal to
of all functions whose weak derivatives of order less than or equal to 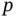 are elements of the Lebesgue space
are elements of the Lebesgue space 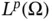 is defined.
is defined.










