Among all the various categories of applications of piezoelectric devices and systems, it is perhaps the piezoelectric sensors that have had the most profound impact on measurement technology infrastructure. As noted above, there are a wide and growing collection of piezoelectric transducers that serve as sensors. These include pressure transducers, load cells or force transducers, torque transducers, acoustic microphones, accelerometers, and vibration sensors. The underlying physical basis of nearly all these sensors is the same: the forces applied on opposite sides of a piezoelectric specimen generate a source of charge that is highly sensitive to the applied force, and the measurement of the charge or current provides an estimate of such forces over extremely high frequencies. Often the bandwidth of such sensors extends to the hundreds of kilohertz range. The diversity of piezoelectrically‐based, commercial microphones available from PCB® is illustrated in Figure 1.7. This figure illustrates that the operating range of these sensors is as high as O(100) kHz, and their sensitivity varies from O(1) mV/Pa to O(10) mV/Pa. The physics underlying a wide range of piezoelectric sensors is studied in Chapters 3, 4, 5, 6, 7, and 8.
1.2.3 Actuators or Motors
Piezoelectric actuators or motors are available commercially at companies such as PCB® or PI Ceramics®, and they have been the topic of research in academia and national laboratories for decades. The most popular commercially available actuators are the linear or stack actuators and the bender actuators. Stack actuators developed by PI Ceramic® are depicted in Figure 1.8. Commercially available stack actuators usually have a small stroke, on the order O(10) to O(100) 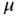 m. These prototypical piezoelectric composites are studied in Chapters 5, 6, 7, and 8. Figure 1.9depicts bender actuators available from PI Ceramics®. The bending actuators are intended for applications that require a larger stroke and operate at a lower frequency than the linear actuators. The stroke of the benders depicted in Figure 1.9varies approximately from O(100) to O(1000)
m. These prototypical piezoelectric composites are studied in Chapters 5, 6, 7, and 8. Figure 1.9depicts bender actuators available from PI Ceramics®. The bending actuators are intended for applications that require a larger stroke and operate at a lower frequency than the linear actuators. The stroke of the benders depicted in Figure 1.9varies approximately from O(100) to O(1000) 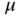 m. Composite bending actuators are studied in Chapters 5, 6, 7, and 8.
m. Composite bending actuators are studied in Chapters 5, 6, 7, and 8.
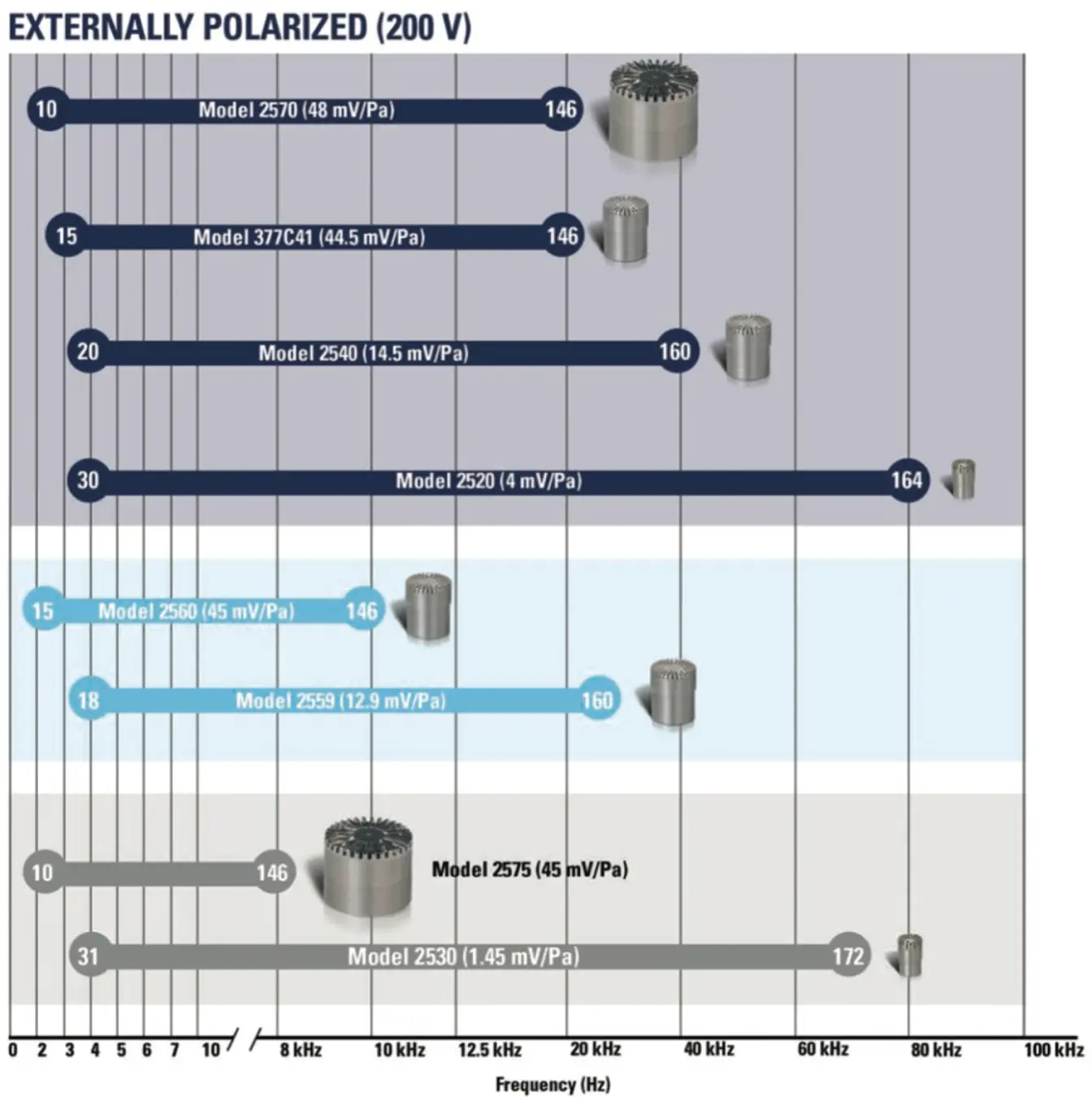
Figure 1.7 Piezoelectrically based microphones from PCB®,
Source: HOW TO SELECT THE BEST TEST & MEASUREMENT PRECISION MICROPHONE, PCB Piezotronics, Inc. Retrieved from: http://www.pcb.com/Microphones Preamplifiers Acoustic Accessories/select.

Figure 1.8 Piezoelectric stack actuators available from PI ceramic®, Source: GmbH & Co. KG owner.

Figure 1.9 Piezoelectric bender actuators available from PI ceramic®, Source: GmbH & Co. KG owner.
The linear and bending actuators shown in Figure 1.8and 1.9are considered in examples throughout this text: they are perhaps the most simple macroscale actuators that are commercially available. In fact, they can also be used to understand the basic physics of piezoelectric sensors too. They illustrate the operating principles of and modeling techniques for piezoelectric composites that are evident in much more complex designs.
Unfortunately, the theoretical underpinnings of piezoelectric mechanics embraces a wide collection of fields of study that must be synthesized. We begin in Chapter 2. Section 2.1reviews the fundamentals of vectors, bases, and frames of reference. This section is vital in developing an understanding of how physical vectors such as velocity, acceleration, stress vectors, electric field vectors, and electric displacement vectors are represented. The section culminates in a presentation of rotation matrices and their essential role in constructing change of bases for different representations of vectors. Section 2.2then extends these results by introducing multilinear operators, or tensors, that act between vector spaces. Since vectors are first order tensors, they are a special case of the tensors presented in Section 2.2. In addition, another collection of physical variables critical to linear piezoelectricity are understood as tensors. These include the stress tensor, linear strain tensor, permittivity tensor, piezoelectric coupling tensor, stiffness tensor, and compliance tensor. The section concludes with a discussion of the role of rotation matrices in the representation and change of basis formula for 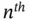 order tensors. Section 2.3discusses symmetry properties and geometric properties of tensors and crystals. The discussion begins with an overview of the geometry of crystals in Section 2.3.1. The 14 Bravais lattices and seven crystal systems are defined, as are the 32 crystallographic point groups. This section concludes with examples of symmetry transformations for typical crystal classes, and a discussion of tensor invariance associated with symmetry operations.
order tensors. Section 2.3discusses symmetry properties and geometric properties of tensors and crystals. The discussion begins with an overview of the geometry of crystals in Section 2.3.1. The 14 Bravais lattices and seven crystal systems are defined, as are the 32 crystallographic point groups. This section concludes with examples of symmetry transformations for typical crystal classes, and a discussion of tensor invariance associated with symmetry operations.
Chapter 3reviews the basics of continuum mechanics that are needed to build a coherent framework for linear piezoelectricity. The definition of the stress tensor in three dimensions is presented in Section 3.1.1, Cauchy's formula is presented in Section 3.1.2, and the equations of equilibrium are discussed in Section 3.1.3. Section 3.2 is dedicated to the study of the linear strain tensor, the mechanical field variable that is complementary to the stress tensor. The general definition of the linear strain tensor in three dimensions is presented, as well as the kinematic relationships for common structures such as the axial rod, Bernoulli–Euler beam, and Kirchoff plate. Strain energy is discussed in Section 3.3. The strain energy density function is introduced, and its role in determining additional symmetry properties of the material stiffness tensor is given. A review of the constitutive laws for linearly elastic materials is summarized in Section 3.4, and the structure of the constitutive relationships for triclinic, orthotropic, and transversely isotropic materials are summarized. The chapter ends with an introduction of the initial‐boundary value problem of linear elasticity in Section 3.5.
We turn to a discussion of continuum electrodynamics in Chapter 4. Charge and current are introduced in Section 4.1, and the static electric and magnetic fields are discussed in Section 4.2. Maxwell's equations are introduced in Equation 4.10 in SI units. Section 4.3.1 relates the polarization and electric displacement vectors, and relates them to bound and mobile charge, respectively. Magnetization and magnetic field intensity are defined in Section 4.3.2, as are the free, bound, and polarization current densities, respectively. Section 4.3.3 discusses the form of Maxwell's equations in Gaussian units, which prove to be convenient for the derivation of the equations of piezoelectricity.
Читать дальше

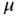 m. These prototypical piezoelectric composites are studied in Chapters 5, 6, 7, and 8. Figure 1.9depicts bender actuators available from PI Ceramics®. The bending actuators are intended for applications that require a larger stroke and operate at a lower frequency than the linear actuators. The stroke of the benders depicted in Figure 1.9varies approximately from O(100) to O(1000)
m. These prototypical piezoelectric composites are studied in Chapters 5, 6, 7, and 8. Figure 1.9depicts bender actuators available from PI Ceramics®. The bending actuators are intended for applications that require a larger stroke and operate at a lower frequency than the linear actuators. The stroke of the benders depicted in Figure 1.9varies approximately from O(100) to O(1000) 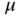 m. Composite bending actuators are studied in Chapters 5, 6, 7, and 8.
m. Composite bending actuators are studied in Chapters 5, 6, 7, and 8.


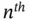 order tensors. Section 2.3discusses symmetry properties and geometric properties of tensors and crystals. The discussion begins with an overview of the geometry of crystals in Section 2.3.1. The 14 Bravais lattices and seven crystal systems are defined, as are the 32 crystallographic point groups. This section concludes with examples of symmetry transformations for typical crystal classes, and a discussion of tensor invariance associated with symmetry operations.
order tensors. Section 2.3discusses symmetry properties and geometric properties of tensors and crystals. The discussion begins with an overview of the geometry of crystals in Section 2.3.1. The 14 Bravais lattices and seven crystal systems are defined, as are the 32 crystallographic point groups. This section concludes with examples of symmetry transformations for typical crystal classes, and a discussion of tensor invariance associated with symmetry operations.










