We also would like to specifically thank Dr. Vijaya V. N. Sriram Malladi and Dr. Sai Tej Paruchuri for their tireless efforts in editing and correcting the draft manuscript. Their meticulous attention to detail, suggestions and tireless effort has made this book a better version from its original draft. Additionally, we would like to thank our students Dr. Sheyda Davaria, Dr. Mohammad Albakri, Manu Krishnan, Mostafa Motaharibidgoli who have worked through the manuscript in order to improve its clarity. We would also like to also thank Sourabh Sangle, Murat Ambarkutuk, Lucas Tarazaga and Vanessa Tarazaga for their help in proofreading the last draft of the document. Finally, we would like to acknowledge anyone else not mentioned that contributed to the manuscript, including the students in our classes who provided valuable input throughout the years.
And, of course, we thank our families for their continued support and encouragement in efforts just like this one over the years.
Andrew J. Kurdila
Pablo A. Tarazaga
Blacksburg, VA
February, 2021
1 Introduction
1.1 The Piezoelectric Effect
In the most general terms, a material is piezoelectric if it transforms electrical into mechanical energy, and vice versa, in a reversible or lossless process. This transformation is evident at a macroscopic scale in what are commonly known as the direct and converse piezoelectric effects. The direct piezoelectric effect refers to the ability of a material to transform mechanical deformations into electrical charge. Equivalently, application of mechanical stress to a piezoelectric specimen induces flow of electricity in the direct piezoelectric effect. The converse piezoelectric effect describes the process by which the application of an electrical potential difference across a specimen results in its deformation. The converse effect can also be viewed as how the application of an external electric field induces mechanical stress in the specimen.
While the brothers Pierre and Jacques Curie discovered piezoelectricity in 1880, much the early impetus motivating its study can be attributed to the demands for submarine countermeasures that evolved during World War I. An excellent and concise history, before, during, and after World War I, can be found in [43]. With the increasing military interest in detecting submarines by their acoustic signatures during World War I, early research often studied naval applications, and specifically sonar. Paul Langevin and Walter Cady had pivotal roles during these early years. Langevin constructed ultrasonic transducers with quartz and steel composites. Shortly thereafter, the use of piezoelectric quartz oscillators became prevalent in ultrasound applications and broadcasting. The research by W.G. Cady was crucial in determining how to employ quartz resonators to stabilize high frequency electrical circuits.
A number of naturally occurring crystalline materials including Rochelle salt, quartz, topaz, tourmaline, and cane sugar exhibit piezoelectric effects. These materials were studied methodically in the early investigations of piezoelectricity. Following World War II, with its high demand for quartz plates, research and development of techniques to synthesize piezoelectric crystalline materials flourished. These efforts have resulted in a wide variety of synthetic piezoelectrics, and materials science research into specialized piezoelectrics continues to this day.
1.1.1 Ferroelectric Piezoelectrics
Perhaps one of the most important classes of piezoelectric materials that have become popular over the past few decades are the ferroelectric dielectrics. A ferroelectric can have coupling between the mechanical and electrical response that is several times a large as that in natural piezoelectrics. Ferroelectrics include materials such as barium titanate and lead zirconate titanate, and their unit cells are depicted in Figure 1.1. When the centers of positive and negative charge in a unit cell of a crystalline material do not coincide, the material is said to be polar or dielectric. An electric dipole moment 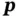 is a vector that points from the center of negative charge to the center of positive charge, and its magnitude is equal to
is a vector that points from the center of negative charge to the center of positive charge, and its magnitude is equal to 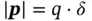 where
where 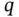 is the magnitude of the charge at the centers and
is the magnitude of the charge at the centers and 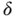 is the separation between the centers. The limiting volumetric density of dipole moments is the polarization vector
is the separation between the centers. The limiting volumetric density of dipole moments is the polarization vector 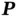 . Intuitively we think of the polarization vector
. Intuitively we think of the polarization vector 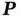 as measuring the asymmetry of the internal electric field of the piezoelectric crystal lattice. Ferroelectrics exhibit spontaneous electric polarization that can be reversed by the application of an external electric field. In other words, the polarization of the material is evident during a spontaneous process, one that evolves to a state that is thermodynamically more stable. Understanding this process requires a discussion of the micromechanics of a ferroelectric.
as measuring the asymmetry of the internal electric field of the piezoelectric crystal lattice. Ferroelectrics exhibit spontaneous electric polarization that can be reversed by the application of an external electric field. In other words, the polarization of the material is evident during a spontaneous process, one that evolves to a state that is thermodynamically more stable. Understanding this process requires a discussion of the micromechanics of a ferroelectric.
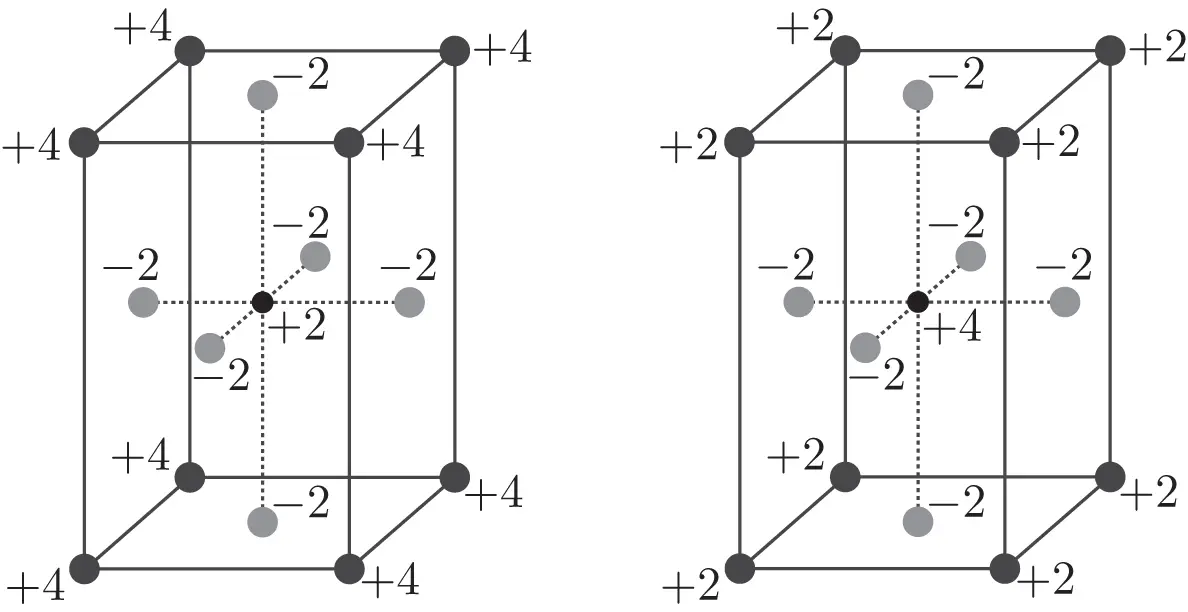
Figure 1.1 Barium titanate and lead zirconate titanate. (Left) Barium titanate  with
with 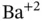 cation at the center,
cation at the center, 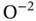 anions on the faces, and
anions on the faces, and 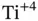 cations at the corners of the unit cell. (Right) Lead zircanate titanate
cations at the corners of the unit cell. (Right) Lead zircanate titanate 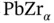
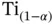
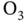 with
with 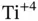 or
or 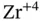 cation at the center,
cation at the center, 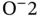 anions on the faces, and
anions on the faces, and 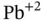 cations at the corners of the unit cell.
cations at the corners of the unit cell.
The micromechanics of ferroelectric dielectrics is subtle and interesting. Above a critical temperature 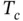 , the Curie temperature, the crystal structure of a ferroelectric is usually symmetric, and a plot of the polarization versus applied electric charge is generally nonlinear and single‐valued as shown in Figure 1.2.
, the Curie temperature, the crystal structure of a ferroelectric is usually symmetric, and a plot of the polarization versus applied electric charge is generally nonlinear and single‐valued as shown in Figure 1.2.
Читать дальше

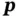 is a vector that points from the center of negative charge to the center of positive charge, and its magnitude is equal to
is a vector that points from the center of negative charge to the center of positive charge, and its magnitude is equal to 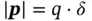 where
where 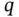 is the magnitude of the charge at the centers and
is the magnitude of the charge at the centers and 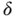 is the separation between the centers. The limiting volumetric density of dipole moments is the polarization vector
is the separation between the centers. The limiting volumetric density of dipole moments is the polarization vector 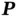 . Intuitively we think of the polarization vector
. Intuitively we think of the polarization vector 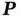 as measuring the asymmetry of the internal electric field of the piezoelectric crystal lattice. Ferroelectrics exhibit spontaneous electric polarization that can be reversed by the application of an external electric field. In other words, the polarization of the material is evident during a spontaneous process, one that evolves to a state that is thermodynamically more stable. Understanding this process requires a discussion of the micromechanics of a ferroelectric.
as measuring the asymmetry of the internal electric field of the piezoelectric crystal lattice. Ferroelectrics exhibit spontaneous electric polarization that can be reversed by the application of an external electric field. In other words, the polarization of the material is evident during a spontaneous process, one that evolves to a state that is thermodynamically more stable. Understanding this process requires a discussion of the micromechanics of a ferroelectric.
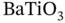 with
with 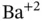 cation at the center,
cation at the center, 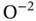 anions on the faces, and
anions on the faces, and 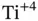 cations at the corners of the unit cell. (Right) Lead zircanate titanate
cations at the corners of the unit cell. (Right) Lead zircanate titanate 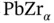
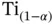
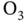 with
with 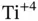 or
or 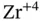 cation at the center,
cation at the center, 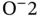 anions on the faces, and
anions on the faces, and 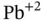 cations at the corners of the unit cell.
cations at the corners of the unit cell.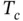 , the Curie temperature, the crystal structure of a ferroelectric is usually symmetric, and a plot of the polarization versus applied electric charge is generally nonlinear and single‐valued as shown in Figure 1.2.
, the Curie temperature, the crystal structure of a ferroelectric is usually symmetric, and a plot of the polarization versus applied electric charge is generally nonlinear and single‐valued as shown in Figure 1.2.










