The phasor form of the E‐field vector of the circularly polarized waves, meeting the above conditions, could be written from equation (4.6.1a)as follows:
(4.6.4) 
The e jωttime‐harmonic factor is suppressed in the above equations. The time‐domain forms of the circularly polarized waves, using the instantaneous 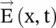 ‐field components, at any location in the positive x‐direction and also at the x = 0, i.e. in the (y‐z)‐plane, are expressed as follows:
‐field components, at any location in the positive x‐direction and also at the x = 0, i.e. in the (y‐z)‐plane, are expressed as follows:
(4.6.5) 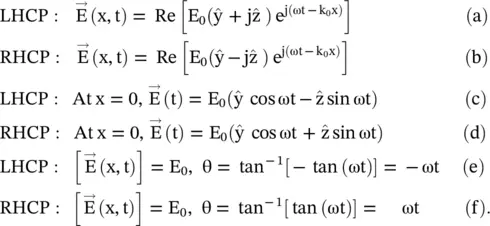
The handedness , i.e. the sense of rotation of the 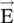 ‐vector of the circularly polarized wave is determined by the direction of rotation of the
‐vector of the circularly polarized wave is determined by the direction of rotation of the 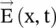 ‐vector in the transverse (y‐z)‐plane with respect to time, whereas the EM‐wave propagates in the x‐direction. Therefore, using equation (4.6.5f), Fig. (4.10b)shows the anti‐clock rotation of the E‐field vector tracing a circle of radius E 0in the (y‐z)‐plane. The sense of rotation is considered with respect to cos(ωt), taking t = 0. It shows the wave propagating in the positive x‐direction, i.e. the wave coming toward an observer standing on the positive x‐axis is the right‐hand circularly polarized wave (RHCP) . Its field vector is given by equation (4.6.4b). Similarly, equation (4.6.5e)shows the clockwise rotation , i.e. the left‐hand circularly polarized wave (LHCP ) propagating in the positive x‐direction. The magnetic fields of the RHCP and LHCP wave are obtained using equation (4.6.4)with equation (4.5.34a):
‐vector in the transverse (y‐z)‐plane with respect to time, whereas the EM‐wave propagates in the x‐direction. Therefore, using equation (4.6.5f), Fig. (4.10b)shows the anti‐clock rotation of the E‐field vector tracing a circle of radius E 0in the (y‐z)‐plane. The sense of rotation is considered with respect to cos(ωt), taking t = 0. It shows the wave propagating in the positive x‐direction, i.e. the wave coming toward an observer standing on the positive x‐axis is the right‐hand circularly polarized wave (RHCP) . Its field vector is given by equation (4.6.4b). Similarly, equation (4.6.5e)shows the clockwise rotation , i.e. the left‐hand circularly polarized wave (LHCP ) propagating in the positive x‐direction. The magnetic fields of the RHCP and LHCP wave are obtained using equation (4.6.4)with equation (4.5.34a):
(4.6.6) 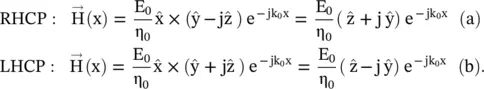
In the case of the wave propagation in the negative x‐direction, i.e. the wave moves away from the observer standing on the positive x‐axis, the role of RHCP and LHCP gets interchanged. Further, the handedness of circular polarization can be reversed by applying 180° phase‐shift to either the y or z component of the 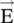 ‐field vector. The circular polarization could be further considered as a linear combination of two linearly polarized waves . Alternatively, the linear polarization can also be considered as a linear combination of the left‐hand and right‐hand circularly polarized waves [B.9].
‐field vector. The circular polarization could be further considered as a linear combination of two linearly polarized waves . Alternatively, the linear polarization can also be considered as a linear combination of the left‐hand and right‐hand circularly polarized waves [B.9].
4.6.3 Elliptical Polarization
Two orthogonal field components, in the space quadrature, of unequal magnitude and arbitrary phase angle (φ) between them, generate the elliptical polarization, i.e. the resultant E‐field vector rotates in the plane of polarization such that its tip traces an elliptical path as shown in Fig. (4.10c). The instantaneous orthogonal E‐field components in the x = 0 plane are given below:
(4.6.7) 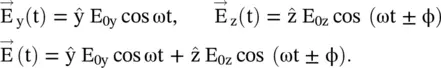
Using the above equation and identity 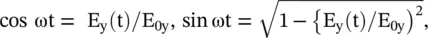 the following equation of the ellipse is obtained:
the following equation of the ellipse is obtained:
(4.6.8) 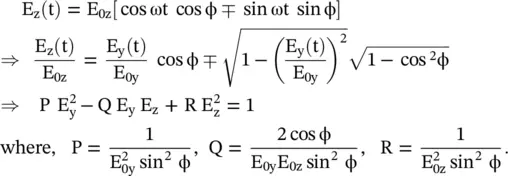
The semi‐major axis OA, the semi‐minor axis OB of the ellipse shown in Fig. (4.10c), and the axial ratio (AR) of the polarization ellipse are given below [B.9, B.29]:
(4.6.9) 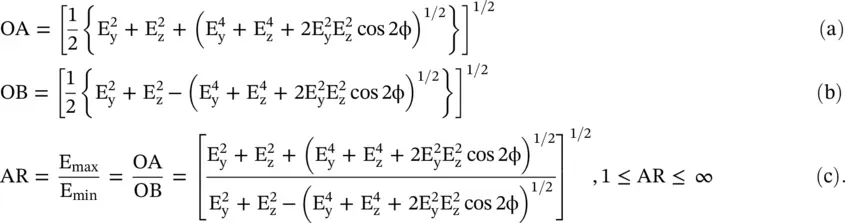
The tilt angle θ of the polarization ellipse, i.e. inclination of the major axis OA with y‐axis is [B.9, B.29]:
(4.6.10) 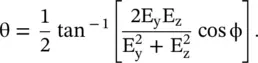
For φ ≠ π/2, the polarization ellipse is inclined with respect to the y‐axis. The linear and circular polarizations are obtained as special cases from the elliptical polarization. For instance, for E z(t) = 0 the wave is horizontally polarized in the y‐direction. For E 0y= E 0z= E 0and φ = ± π/2, the LHCP/RHCP wave is obtained as equation (4.6.9)is reduced to an equation of a circle with OA = OB. For the linear polarization, AR is infinity. However, for the circular polarization, AR is unity. In the case E 0y= E 0z= E 0and φ ≠ π/2, the wave is not circularly polarized and its AR is cotφ/2. For a practical circularly polarized antenna, the axial ratio is frequency‐dependent and its axial ratio bandwidth is defined as the frequency band over which AR ≤ 3dB.
4.6.4 Jones Matrix Description of Polarization States
The polarizing devices change the state of polarization. For instance, the polarizing devices could change the rotation of the linear polarization or convert the linear polarization into circular polarization. The Jones matrix method describes and manipulates the polarization states of the EM‐wave using a 2 × 1 column vector, known as the Jones vector and transfer matrix of the polarizing device, known as the Jones matrix [B.30, B.31]. The Jones matrix is used in chapter‐22 with metasurfaces.
The polarization state of the EM‐wave propagation in the x‐direction is given by equation (4.6.1). The orthogonal E‐field components can be expressed in the form of the following column vector, known as the Jones vector :
(4.6.11) 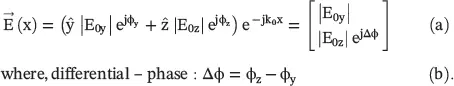
In the above expression, the common phase angle has been absorbed in the propagation factor 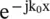 . The Jones vector describes polarization states of any plane wave field. Some common polarization states are summarized below with respect to Fig. (4.10):
. The Jones vector describes polarization states of any plane wave field. Some common polarization states are summarized below with respect to Fig. (4.10):
(4.6.12) 
In the above expressions, the normalized magnitude of the E‐field components are |E oy| = |E oz| = 1.
Читать дальше


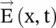 ‐field components, at any location in the positive x‐direction and also at the x = 0, i.e. in the (y‐z)‐plane, are expressed as follows:
‐field components, at any location in the positive x‐direction and also at the x = 0, i.e. in the (y‐z)‐plane, are expressed as follows: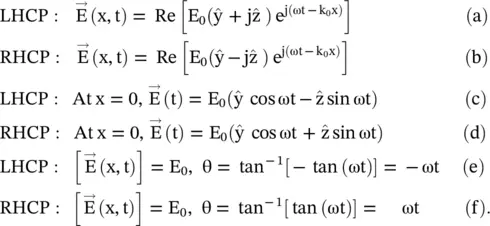
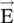 ‐vector of the circularly polarized wave is determined by the direction of rotation of the
‐vector of the circularly polarized wave is determined by the direction of rotation of the 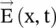 ‐vector in the transverse (y‐z)‐plane with respect to time, whereas the EM‐wave propagates in the x‐direction. Therefore, using equation (4.6.5f), Fig. (4.10b)shows the anti‐clock rotation of the E‐field vector tracing a circle of radius E 0in the (y‐z)‐plane. The sense of rotation is considered with respect to cos(ωt), taking t = 0. It shows the wave propagating in the positive x‐direction, i.e. the wave coming toward an observer standing on the positive x‐axis is the right‐hand circularly polarized wave (RHCP) . Its field vector is given by equation (4.6.4b). Similarly, equation (4.6.5e)shows the clockwise rotation , i.e. the left‐hand circularly polarized wave (LHCP ) propagating in the positive x‐direction. The magnetic fields of the RHCP and LHCP wave are obtained using equation (4.6.4)with equation (4.5.34a):
‐vector in the transverse (y‐z)‐plane with respect to time, whereas the EM‐wave propagates in the x‐direction. Therefore, using equation (4.6.5f), Fig. (4.10b)shows the anti‐clock rotation of the E‐field vector tracing a circle of radius E 0in the (y‐z)‐plane. The sense of rotation is considered with respect to cos(ωt), taking t = 0. It shows the wave propagating in the positive x‐direction, i.e. the wave coming toward an observer standing on the positive x‐axis is the right‐hand circularly polarized wave (RHCP) . Its field vector is given by equation (4.6.4b). Similarly, equation (4.6.5e)shows the clockwise rotation , i.e. the left‐hand circularly polarized wave (LHCP ) propagating in the positive x‐direction. The magnetic fields of the RHCP and LHCP wave are obtained using equation (4.6.4)with equation (4.5.34a):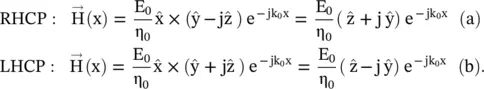
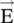 ‐field vector. The circular polarization could be further considered as a linear combination of two linearly polarized waves . Alternatively, the linear polarization can also be considered as a linear combination of the left‐hand and right‐hand circularly polarized waves [B.9].
‐field vector. The circular polarization could be further considered as a linear combination of two linearly polarized waves . Alternatively, the linear polarization can also be considered as a linear combination of the left‐hand and right‐hand circularly polarized waves [B.9].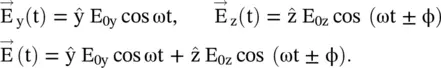
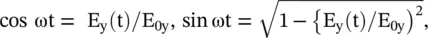 the following equation of the ellipse is obtained:
the following equation of the ellipse is obtained: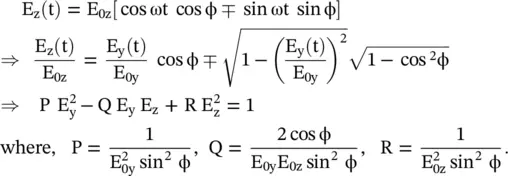
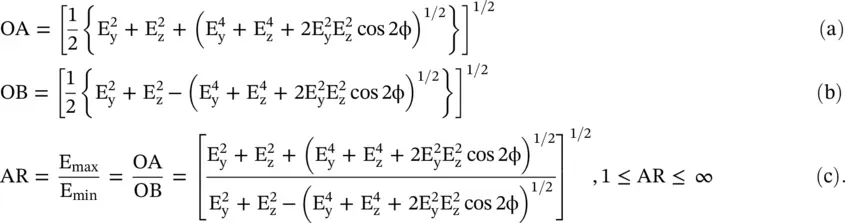
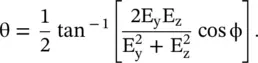
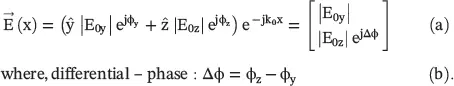
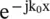 . The Jones vector describes polarization states of any plane wave field. Some common polarization states are summarized below with respect to Fig. (4.10):
. The Jones vector describes polarization states of any plane wave field. Some common polarization states are summarized below with respect to Fig. (4.10):











