Anand K. Verma - Introduction To Modern Planar Transmission Lines

The wave equations (4.5.13a)and (4.5.13b), for the E yand H zfield components, are solved to get the total solution as a superposition of two waves traveling in opposite directions:

(4.5.28)

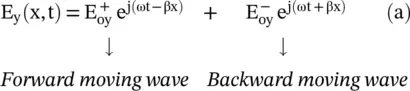
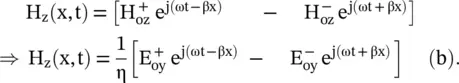
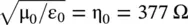In the above expression, is the intrinsic or characteristic impedance, of the uniform plane in free space. The power movement is obtained from the Poynting vector 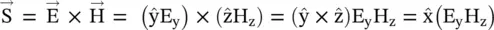. The power of the forward wave travels in the positive x‐direction. The direction of the power movement is the direction of the group velocity . In the x‐direction, the direction of the phase velocity is associated with the direction of the propagation vector , i.e. the wavenumber .

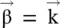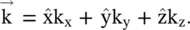Figure (4.9d)shows the propagating EM‐wave in an arbitrary direction of the wavevector The wavevector 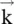is normal to the equiphase surface. The position vector of a point P at the equiphase surface is 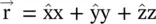. The following expressions describe the propagating wave as a solution to the wave equations (4.5.12a)and (4.5.12c):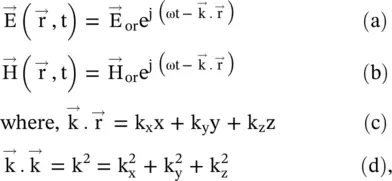

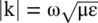(4.5.29)

where . Equation (4.5.29d)is the dispersion equation . In the above equations, field quantities show time dependence, i.e. temporal dependence , through factor e jωtand space dependence, i.e. spatial dependence , through factor 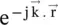. It also shows the lagging phase of the propagating wave in the positive direction. This is the convention adopted by engineers. On several occasions, physicist prefers an alternative sign convention, i.e. e −jωtand 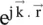. It leads to a leading phase for propagating waves in a positive direction. A reader must be careful while reading literature from several sources. For y‐polarized wave propagating in the x‐direction with k y= k z= 0 and k x= β x− jα, the solution of the wave equation could be written as follows: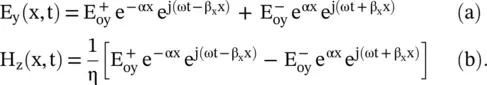

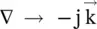(4.5.30)

The second terms of the above equations show wave propagation in the negative x‐direction. The wave equations show the decaying propagating waves. For the case α = 0, the above equations are the same as that of equations (4.5.28).

Maxwell’s equations in the unbounded medium could be also written in the vector algebraic form . The del operator can be replaced as follows: . Using equation (4.4.9), for the charge‐free lossless medium ρ = σ = 0, two sets of Maxwell equations, for the isotropic and anisotropic media, are written in the following algebraic forms: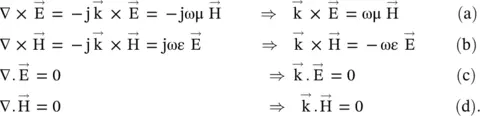

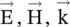Set #I for the isotropic medium :

Set #II for the anisotropic medium :

(4.5.31)

Equations (4.5.31a)and (4.5.31b)show that for the positive values of μ and ε , the triplet follows the right‐handed orthogonal coordinate system . Equations (4.5.31c)and (4.5.31d)show that in an isotropic medium, the field vectors 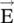and 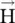are orthogonal to the wavevector 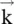. Equations (4.5.31c)and (4.5.31d)directly follow from the first two Maxwell equations by taking their dot product with the wavevector 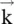. Equation (4.5.31a)further shows that 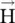is normal to both 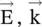vectors, and equation (4.5.31b)shows that is normal to both vectors. In brief, the vectors 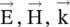are orthogonal to each other, and there is no field component along the wavevector 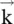,i.e. the wave is a transverse electromagnetic (TEM) type . Also, in an isotropic medium, 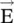is parallel to vector 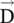and 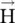is parallel to vector . This statement does not hold for the anisotropic medium . Maxwell equations (4.5.31e)– (4.5.31h)apply to an anisotropic medium. In an anisotropic medium, equations (4.5.31e)and (4.5.31f)show that 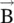is normal to vectors 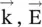and 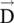is normal to vectors 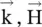. However, 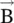is not parallel to 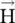. Also, 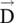is not parallel to 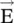. It is discussed in subsection (4.2.3).