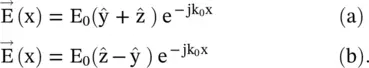The field decreases by a factor e −αx ,whereas the wave travels through a lossy medium. If the wave travels a distance x = δ = 1/α, known as the skin depth, the field is decreased by 1/e of its initial strength, i.e. approximately 37% of its initial field strength. However, the power decreases at a faster rate, i.e. by the factor e −2αx. If the initial power density is S 0, the power density at distance x is
(4.5.44) 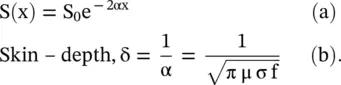
The attenuation constant α in the above equation is used from equation (4.5.35b). The power loss of wave traveling a distance x is computed after computing the power loss at unit distance x = 1m:
(4.5.45) 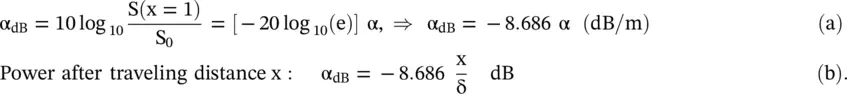
In the above equation, the value of e is 2.71828. The power loss is about 9 dB per skin‐depth. The attenuation constant α of a lossy medium is defined by equation (4.5.44a)as follows:
(4.5.46) 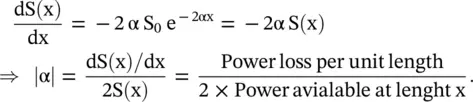
4.6 Polarization of EM‐waves
The uniform plane wave in the unbounded medium is the TEM‐type wave. The monochromatic EM‐wave is characterized by amplitude , phase , and polarization states . The microwave to optical wave devices can appropriately manipulate these characteristics to steer the EM‐waves in the desired direction with shaped wavefront. The modern metasurfaces, discussed in sections (22.5) and (22.6) of chapter 22, can achieve such controls on the reflected and transmitted waves.
In general, both 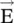 and
and 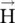 fields have two orthogonal field components in a plane normal to the direction of propagation, the x‐direction, as shown in Fig. (4.9a and b). The field components are in the (y‐z)‐plane. For the TEM mode, it is possible to get either (E y, H z) or (E z, H y) pair of fields. Both pairs of field components can also exist. The orientation of the electric field component and the movement of the tip of the resultant E‐field determine the polarization of the EM‐wave. Thus, the (E y, H z) pair of the EM‐wave is called a y ‐polarized wave, as only the E ycomponent of wave exists. The (E z, H y) pair of the EM‐wave is called the z‐polarized wave . The (y‐z)‐plane is known as the plane of polarization . It is normal to the direction of propagation, i.e. the x‐axis. Both these polarizations are linear polarization .
fields have two orthogonal field components in a plane normal to the direction of propagation, the x‐direction, as shown in Fig. (4.9a and b). The field components are in the (y‐z)‐plane. For the TEM mode, it is possible to get either (E y, H z) or (E z, H y) pair of fields. Both pairs of field components can also exist. The orientation of the electric field component and the movement of the tip of the resultant E‐field determine the polarization of the EM‐wave. Thus, the (E y, H z) pair of the EM‐wave is called a y ‐polarized wave, as only the E ycomponent of wave exists. The (E z, H y) pair of the EM‐wave is called the z‐polarized wave . The (y‐z)‐plane is known as the plane of polarization . It is normal to the direction of propagation, i.e. the x‐axis. Both these polarizations are linear polarization .
Figure (4.9a and c)show that for the EM‐wave propagating in the x‐direction, the tip of the E yfield component moves along the y‐axis from +E 0to 0 to −E 0. The movement and rotation of the tip of the 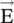 ‐vector could be seen using the instantaneous
‐vector could be seen using the instantaneous 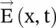 ‐vector of the wave propagating in the x‐direction. In Fig. (4.9c), the path of the tip of the E y‐field vector, in the plane of polarization, traces a line with respect to time. The linear trace demonstrates the vertical linear polarization . However, if both E yand E zfield components are present, any of the three kinds of wave polarizations can be obtained: (i) linear polarization, (ii) circular polarization, and (iii) elliptical polarization . These polarizations are shown in Fig. (4.10a–c). The type of wave polarization depends upon the magnitude and the relative phase of the orthogonal E yand E zfield components. The polarization states are briefly discussed below. Finally, the Jones vector and Jones matrix descriptions are summarized to describe elegantly the polarization states and their control by the polarizing devices.
‐vector of the wave propagating in the x‐direction. In Fig. (4.9c), the path of the tip of the E y‐field vector, in the plane of polarization, traces a line with respect to time. The linear trace demonstrates the vertical linear polarization . However, if both E yand E zfield components are present, any of the three kinds of wave polarizations can be obtained: (i) linear polarization, (ii) circular polarization, and (iii) elliptical polarization . These polarizations are shown in Fig. (4.10a–c). The type of wave polarization depends upon the magnitude and the relative phase of the orthogonal E yand E zfield components. The polarization states are briefly discussed below. Finally, the Jones vector and Jones matrix descriptions are summarized to describe elegantly the polarization states and their control by the polarizing devices.
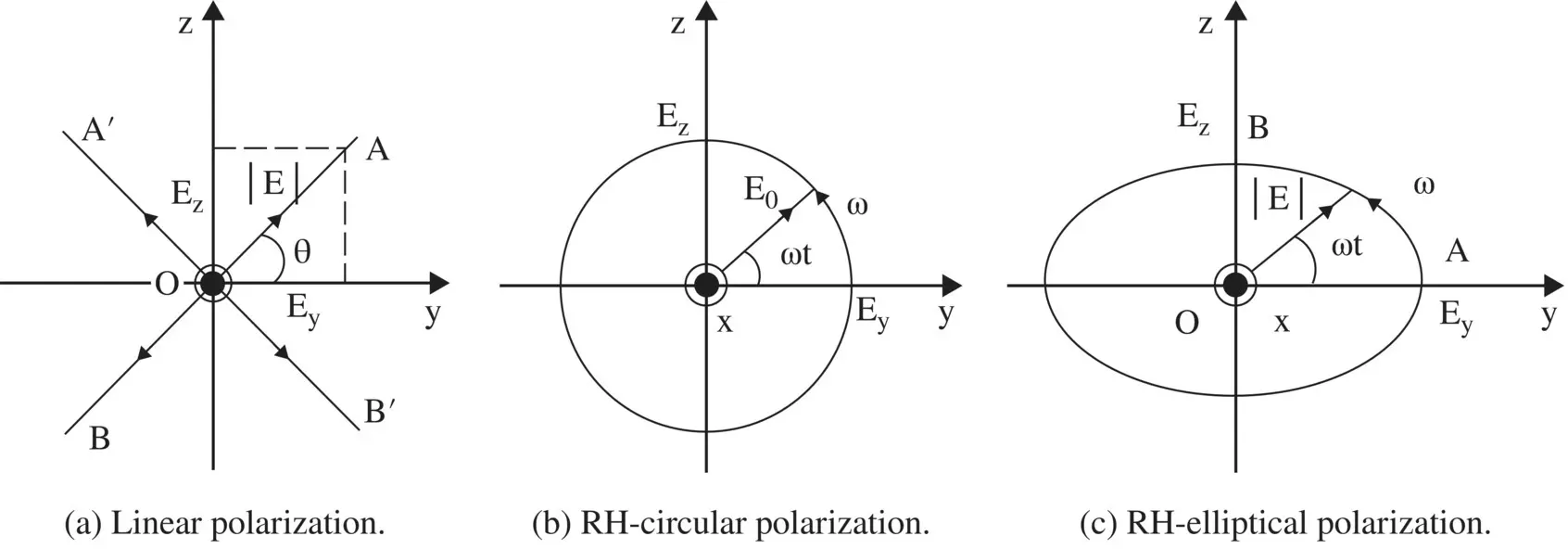
Figure 4.10 Type of polarizations.
4.6.1 Linear Polarization
Figure (4.10a)shows E yand E zfield components of the EM‐wave propagating in the x‐direction. The E‐electric field vector in the (y‐z)‐plane could be written in the phasor form as follows:
(4.6.1) 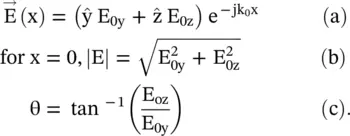
The e jωttime‐harmonic factor is suppressed in the above equation (4.6.1a). Equation (4.6.1b)shows the magnitude of the E‐field, and equation (4.6.1c)computes its inclination with respect to the y‐axis. For y‐polarized wave, E 0z= 0, and for the z‐polarized wave, E 0y= 0. In general, the field components E 0yand E 0zare complex quantities. For the in‐phase field components, these are expressed as E 0y=|E 0y| e jφand E 0z=|E 0z| e jφ. The instantaneous field components are considered to trace the movement of the tip of the 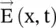 ‐vector:
‐vector:
(4.6.2) 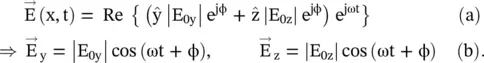
In the above equations, both field components have an identical phase (ωt + φ). Figure (4.10a)shows the slant or inclined linearly polarized wave with the in‐phase E yand E zcomponents. The tip of the electric vector ( 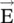 ) moves along line A‐O‐B with respect to time. However, the slant angle θ does not change with time. If both the E‐field components are either in‐phase (A − O − B) or out of phase (A /− O − B /) and have the same magnitude, i.e. E 0y= E 0z= E 0, the corresponding inclination angle of the linear polarization trace, with respect to the y‐axis, is θ = 45° and 135°, respectively. For the linear polarization, the total E‐field given by equation (4.6.1a)could also be written as follows:
) moves along line A‐O‐B with respect to time. However, the slant angle θ does not change with time. If both the E‐field components are either in‐phase (A − O − B) or out of phase (A /− O − B /) and have the same magnitude, i.e. E 0y= E 0z= E 0, the corresponding inclination angle of the linear polarization trace, with respect to the y‐axis, is θ = 45° and 135°, respectively. For the linear polarization, the total E‐field given by equation (4.6.1a)could also be written as follows:
(4.6.3) 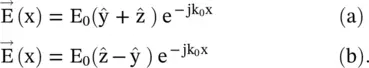
4.6.2 Circular Polarization
The circular polarization, shown in Fig. (4.10b), is obtained for two orthogonal field components of equal magnitude, and phase in quadrature. So, to get the circular polarization, two electric field components oscillate at the same frequency and meet the following conditions:
Equal amplitude: The magnitudes of Ey and Ez are equal, i.e. |E0y| = |E0z| = E0.
Space quadrature: The Ey and Ez field components are normal to each other.
Time (phase) quadrature: The phase difference between the Ey and Ez field components are (φ = ± 90°), i.e. E0y = E0, and E0z = E0e±π/2 = ± j E0.
Читать дальше

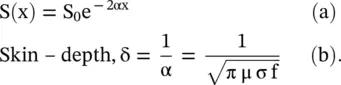
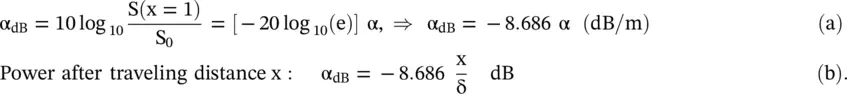
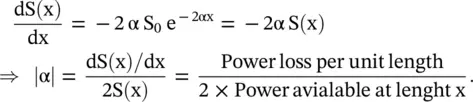
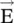 and
and 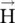 fields have two orthogonal field components in a plane normal to the direction of propagation, the x‐direction, as shown in Fig. (4.9a and b). The field components are in the (y‐z)‐plane. For the TEM mode, it is possible to get either (E y, H z) or (E z, H y) pair of fields. Both pairs of field components can also exist. The orientation of the electric field component and the movement of the tip of the resultant E‐field determine the polarization of the EM‐wave. Thus, the (E y, H z) pair of the EM‐wave is called a y ‐polarized wave, as only the E ycomponent of wave exists. The (E z, H y) pair of the EM‐wave is called the z‐polarized wave . The (y‐z)‐plane is known as the plane of polarization . It is normal to the direction of propagation, i.e. the x‐axis. Both these polarizations are linear polarization .
fields have two orthogonal field components in a plane normal to the direction of propagation, the x‐direction, as shown in Fig. (4.9a and b). The field components are in the (y‐z)‐plane. For the TEM mode, it is possible to get either (E y, H z) or (E z, H y) pair of fields. Both pairs of field components can also exist. The orientation of the electric field component and the movement of the tip of the resultant E‐field determine the polarization of the EM‐wave. Thus, the (E y, H z) pair of the EM‐wave is called a y ‐polarized wave, as only the E ycomponent of wave exists. The (E z, H y) pair of the EM‐wave is called the z‐polarized wave . The (y‐z)‐plane is known as the plane of polarization . It is normal to the direction of propagation, i.e. the x‐axis. Both these polarizations are linear polarization . ‐vector could be seen using the instantaneous
‐vector could be seen using the instantaneous 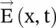 ‐vector of the wave propagating in the x‐direction. In Fig. (4.9c), the path of the tip of the E y‐field vector, in the plane of polarization, traces a line with respect to time. The linear trace demonstrates the vertical linear polarization . However, if both E yand E zfield components are present, any of the three kinds of wave polarizations can be obtained: (i) linear polarization, (ii) circular polarization, and (iii) elliptical polarization . These polarizations are shown in Fig. (4.10a–c). The type of wave polarization depends upon the magnitude and the relative phase of the orthogonal E yand E zfield components. The polarization states are briefly discussed below. Finally, the Jones vector and Jones matrix descriptions are summarized to describe elegantly the polarization states and their control by the polarizing devices.
‐vector of the wave propagating in the x‐direction. In Fig. (4.9c), the path of the tip of the E y‐field vector, in the plane of polarization, traces a line with respect to time. The linear trace demonstrates the vertical linear polarization . However, if both E yand E zfield components are present, any of the three kinds of wave polarizations can be obtained: (i) linear polarization, (ii) circular polarization, and (iii) elliptical polarization . These polarizations are shown in Fig. (4.10a–c). The type of wave polarization depends upon the magnitude and the relative phase of the orthogonal E yand E zfield components. The polarization states are briefly discussed below. Finally, the Jones vector and Jones matrix descriptions are summarized to describe elegantly the polarization states and their control by the polarizing devices.
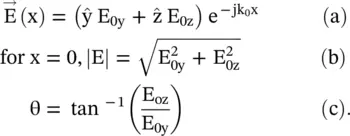
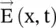 ‐vector:
‐vector: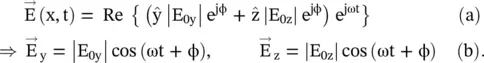
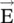 ) moves along line A‐O‐B with respect to time. However, the slant angle θ does not change with time. If both the E‐field components are either in‐phase (A − O − B) or out of phase (A /− O − B /) and have the same magnitude, i.e. E 0y= E 0z= E 0, the corresponding inclination angle of the linear polarization trace, with respect to the y‐axis, is θ = 45° and 135°, respectively. For the linear polarization, the total E‐field given by equation (4.6.1a)could also be written as follows:
) moves along line A‐O‐B with respect to time. However, the slant angle θ does not change with time. If both the E‐field components are either in‐phase (A − O − B) or out of phase (A /− O − B /) and have the same magnitude, i.e. E 0y= E 0z= E 0, the corresponding inclination angle of the linear polarization trace, with respect to the y‐axis, is θ = 45° and 135°, respectively. For the linear polarization, the total E‐field given by equation (4.6.1a)could also be written as follows: