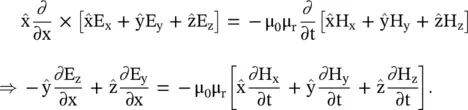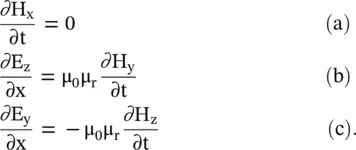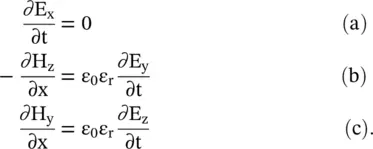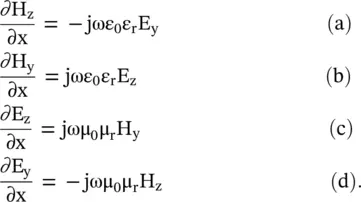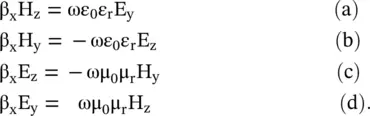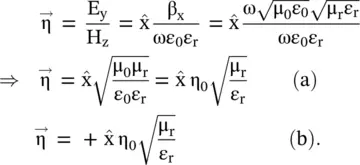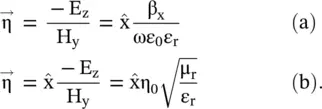(4.5.19) 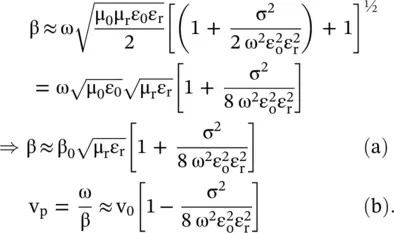
In the above equation, 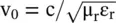 is the velocity of the EM‐wave in the lossless dielectric medium. The presence of the loss has decreased the phase velocity, i.e. a lossy medium supports the dispersive slow‐wave propagation. The use of α and β from equations (4.5.11a) and (4.5.11b)provide more accurate results. The dispersion in a medium is always associated with loss. This fundamental property is further discussed in chapter 6.
is the velocity of the EM‐wave in the lossless dielectric medium. The presence of the loss has decreased the phase velocity, i.e. a lossy medium supports the dispersive slow‐wave propagation. The use of α and β from equations (4.5.11a) and (4.5.11b)provide more accurate results. The dispersion in a medium is always associated with loss. This fundamental property is further discussed in chapter 6.
4.5.3 Uniform Plane Waves in Linear Lossless Homogeneous Isotropic Medium
Figure (4.9a)shows the propagation of the TEM wave in the x‐direction of an unbounded medium. Figure (4.9b)further shows that for the TEM wave, electric and magnetic field components, i.e. the pairs (E y, H z), or (E z, H y), are transverse to the direction of propagation, i.e. ± x ‐ direction. For the field pair (E y, H z), the wave is y‐polarized; and for the field pair(E z, H y), it is the z‐polarized. The polarization of an EM‐wave is determined by the direction of the 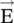 vector. The propagating wave is called the uniform plane wave , as amplitudes of electric and magnetic fields are constant over the equiphase surfaces. Figure (4.9c)shows that the phases of the E yfield at any instant of time, over the equiphase surfaces, are either 0° or 180°. The (y‐z)‐plane is the equiphase surface.
vector. The propagating wave is called the uniform plane wave , as amplitudes of electric and magnetic fields are constant over the equiphase surfaces. Figure (4.9c)shows that the phases of the E yfield at any instant of time, over the equiphase surfaces, are either 0° or 180°. The (y‐z)‐plane is the equiphase surface.
The field components of a uniform plane wave do not change with y and z coordinates, i.e. ∂ /∂y(field E or H) = ∂ /∂z(field E or H) = 0. The field components are a function of x only. So, the field components of the EM‐wave propagating in the x‐direction can be written as follows:
(4.5.20) 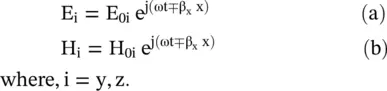
In the above expressions, the (−) sign shows the wave propagation in the positive x‐direction, whereas the (+) sign is for the wave propagation in the negative x‐direction. The wave propagation in the positive x‐direction is discussed below.

Figure 4.9 TEM mode wave in an unbounded medium.
The above expressions related to a uniform plane wave, in an external source‐free 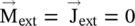 lossless
lossless 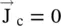 medium, can be applied to the Maxwell equations (4.4.1). In the present case, the del operator is replaced by a derivative with respect to x, i.e.
medium, can be applied to the Maxwell equations (4.4.1). In the present case, the del operator is replaced by a derivative with respect to x, i.e. 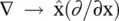 as a derivative with respect to y and z are zero. Maxwell first curl equation is reduced to a simpler form:
as a derivative with respect to y and z are zero. Maxwell first curl equation is reduced to a simpler form:
(4.5.21) 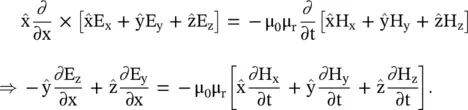
On separating each component of the fields, the following expressions are obtained:
(4.5.22) 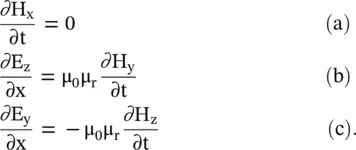
Likewise, the following expressions are obtained from Maxwell's second curl expression (4.4.1b):
(4.5.23) 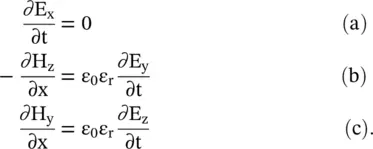
It is seen from the above equations that the E xand H xcomponents, in the direction of propagation, are time‐independent, i.e. constant. They do not play any role in the wave propagation and can be assumed to be zero, without affecting the wave propagation [B.3]. Only transverse field components play a role in wave propagation. The time‐varying H ycomponent generates the E z, whereas the time‐varying E ycomponent generates the H z. It is also true for another time‐varying pair (H z, E z). Maxwell divergence relations also show ∂ E x/∂x = ∂ H x/∂x = 0. Again, E xand H xcomponents do not show any variation along the direction of propagation that is essential for wave propagation. So, in the TEM mode propagation, the longitudinal field components are zero, i.e. E x= H x= 0.
By using equation (4.5.20)with the above equations, the time‐harmonic fields are rewritten as follows:
(4.5.24) 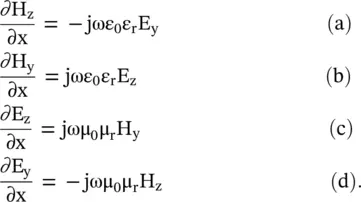
On using equation (4.5.20)with the above equations, the following algebraic expressions are obtained for the EM‐wave propagating in the positive x‐direction:
(4.5.25) 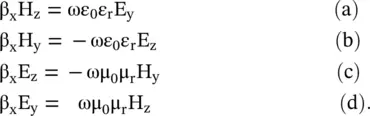
The wave impedance in free space, or in homogeneous unbounded medium, is defined in a plane normal to the direction of propagation [B.2]. For instance, Fig. (4.9a)shows the direction of propagation is along the x‐axis, and wave impedance is defined in the (y‐z) plane. It is also called the intrinsic impedance η 0of free space and intrinsic impedance η of material filled homogeneous space. The following expression is obtained for the wave impedance η, for y‐polarized waves, from equation (4.5.25a):
(4.5.26) 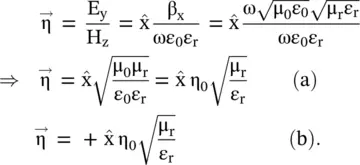
Equation (4.5.25b)provides the following wave impedance for the z‐polarized waves:
(4.5.27) 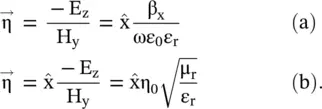
The positive wave impedance of the (E y, H z) or (−E z, H y) fields corresponds to a wave traveling in the +x direction. However, for the (E z, H y) fields, the wave impedance is negative showing the wave propagation in the negative x‐direction. Under certain conditions, a medium can have an imaginary value of propagation constant, i.e. β x= − jp. In this case, the wave impedance becomes reactive, and there is no wave propagation. Again, the wave equation (4.5.20)is reduced to E i= E 0ie −pxe jωtand H i= H 0ie −pxe jωtfor the wave propagation in the positive x‐direction. These are decaying nonpropagating evanescent mode waves. These are only decaying oscillations.
Читать дальше


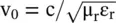 is the velocity of the EM‐wave in the lossless dielectric medium. The presence of the loss has decreased the phase velocity, i.e. a lossy medium supports the dispersive slow‐wave propagation. The use of α and β from equations (4.5.11a) and (4.5.11b)provide more accurate results. The dispersion in a medium is always associated with loss. This fundamental property is further discussed in chapter 6.
is the velocity of the EM‐wave in the lossless dielectric medium. The presence of the loss has decreased the phase velocity, i.e. a lossy medium supports the dispersive slow‐wave propagation. The use of α and β from equations (4.5.11a) and (4.5.11b)provide more accurate results. The dispersion in a medium is always associated with loss. This fundamental property is further discussed in chapter 6.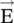 vector. The propagating wave is called the uniform plane wave , as amplitudes of electric and magnetic fields are constant over the equiphase surfaces. Figure (4.9c)shows that the phases of the E yfield at any instant of time, over the equiphase surfaces, are either 0° or 180°. The (y‐z)‐plane is the equiphase surface.
vector. The propagating wave is called the uniform plane wave , as amplitudes of electric and magnetic fields are constant over the equiphase surfaces. Figure (4.9c)shows that the phases of the E yfield at any instant of time, over the equiphase surfaces, are either 0° or 180°. The (y‐z)‐plane is the equiphase surface.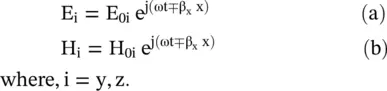

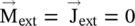 lossless
lossless 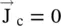 medium, can be applied to the Maxwell equations (4.4.1). In the present case, the del operator is replaced by a derivative with respect to x, i.e.
medium, can be applied to the Maxwell equations (4.4.1). In the present case, the del operator is replaced by a derivative with respect to x, i.e. 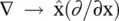 as a derivative with respect to y and z are zero. Maxwell first curl equation is reduced to a simpler form:
as a derivative with respect to y and z are zero. Maxwell first curl equation is reduced to a simpler form: