Anand K. Verma - Introduction To Modern Planar Transmission Lines
Здесь есть возможность читать онлайн «Anand K. Verma - Introduction To Modern Planar Transmission Lines» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Introduction To Modern Planar Transmission Lines
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:4 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Introduction To Modern Planar Transmission Lines: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Introduction To Modern Planar Transmission Lines»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
rovides a comprehensive discussion of planar transmission lines and their applications, focusing on physical understanding, analytical approach, and circuit models
Planar transmission lines form the core of the modern high-frequency communication, computer, and other related technology. This advanced text gives a complete overview of the technology and acts as a comprehensive tool for radio frequency (RF) engineers that reflects a linear discussion of the subject from fundamentals to more complex arguments.
Introduction to Modern Planar Transmission Lines: Physical, Analytical, and Circuit Models Approach Emphasizes modeling using physical concepts, circuit-models, closed-form expressions, and full derivation of a large number of expressions Explains advanced mathematical treatment, such as the variation method, conformal mapping method, and SDA Connects each section of the text with forward and backward cross-referencing to aid in personalized self-study
is an ideal book for senior undergraduate and graduate students of the subject. It will also appeal to new researchers with the inter-disciplinary background, as well as to engineers and professionals in industries utilizing RF/microwave technologies.

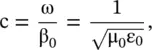
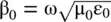 is the propagation constant, i.e. the wavenumber (k 0) in free space. A lossless material medium is electrically characterized by (ε r, μ r). However, it is also characterized by the refractive index
is the propagation constant, i.e. the wavenumber (k 0) in free space. A lossless material medium is electrically characterized by (ε r, μ r). However, it is also characterized by the refractive index 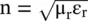 . In the case of a dielectric medium, it is
. In the case of a dielectric medium, it is 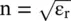 . The velocity of the EM‐wave propagation in a medium is
. The velocity of the EM‐wave propagation in a medium is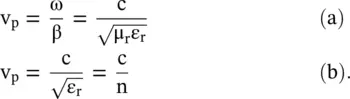
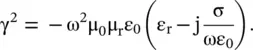
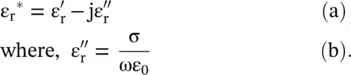
 in a lossy dielectric medium, with the following expressions for the loss‐tangent and propagation constant:
in a lossy dielectric medium, with the following expressions for the loss‐tangent and propagation constant: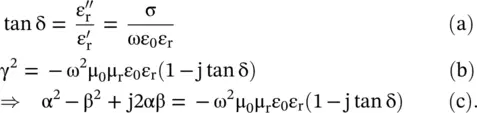
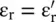 .
.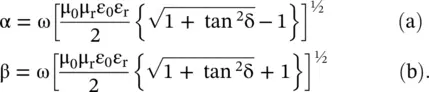
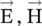 ) fields in a lossy and lossless (α = 0) media are rewritten below:
) fields in a lossy and lossless (α = 0) media are rewritten below: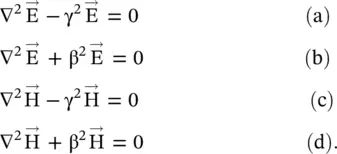
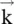 . Sometimes in place of the complex propagation constant γ, the complex wavevector k is used as a complex propagation constant, i.e. k *= β − jα. On using the complex k, the field is written as E 0e −jkx= E 0e −j(β − jα)x= (E 0e −αx) e −jβx.
. Sometimes in place of the complex propagation constant γ, the complex wavevector k is used as a complex propagation constant, i.e. k *= β − jα. On using the complex k, the field is written as E 0e −jkx= E 0e −j(β − jα)x= (E 0e −αx) e −jβx.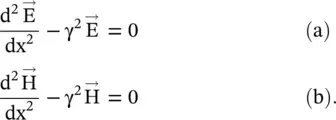
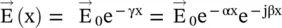 . The time‐harmonic wave propagating in the x‐direction is
. The time‐harmonic wave propagating in the x‐direction is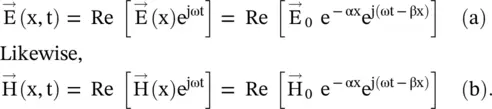
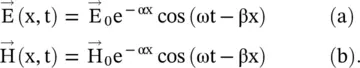
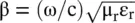 . In the case of low conductivity, i.e. the low‐loss medium, the approximation tan δ ≪ 1, or (σ/ωε 0ε r) ≪ 1, can be used. In such a medium σ ≪ ωε 0ε r ,the contribution of the conduction current is small as compared to that of the displacement current. Such a medium is a dielectric medium with a small loss. On approximating,
. In the case of low conductivity, i.e. the low‐loss medium, the approximation tan δ ≪ 1, or (σ/ωε 0ε r) ≪ 1, can be used. In such a medium σ ≪ ωε 0ε r ,the contribution of the conduction current is small as compared to that of the displacement current. Such a medium is a dielectric medium with a small loss. On approximating, 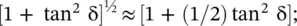 the following expression is obtained from equation (4.5.11a):
the following expression is obtained from equation (4.5.11a):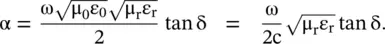
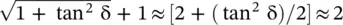 is used to get an approximate value of β for such medium from equation (4.5.11b):
is used to get an approximate value of β for such medium from equation (4.5.11b):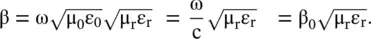
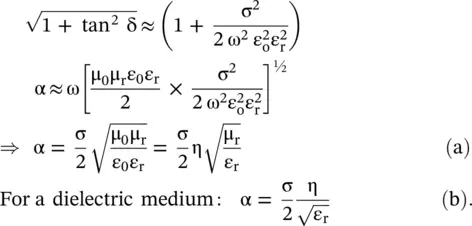
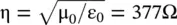 is the characteristic ( intrinsic ) impedance of free space. A low‐loss medium is a mildly dispersive medium, with the frequency‐dependent phase velocity:
is the characteristic ( intrinsic ) impedance of free space. A low‐loss medium is a mildly dispersive medium, with the frequency‐dependent phase velocity:










