(4.7.5) 
Equation (4.7.5a)is a 1D wave equation of the y‐polarized electric field E y≠ 0 and E z= 0. The magnetic field component H zis along the z‐axis. The E yfield component causes polarization in the dielectric medium creating relative permittivity ε r‖along the y‐axis. Further, the electric field E yis transverse to the (x‐z)‐plane containing the direction of propagation x. Such waves are called the transverse electric (TE) waves . The z‐polarized electric field with E z≠ 0 and E y= 0 follows the wave equation (4.7.5b). The E zcomponent generates another polarization in the dielectric medium creating relative permittivity ε r⊥along the z‐axis. In this case, H y‐component is transverse to the (x‐z)‐plane. These waves are called the transverse magnetic (TM) waves . In the present case, also in the case of the oblique incident of the plane waves, the waves are still TEM only. However, the TE and TM terminology is normally used for the non‐TEM mode waves supported by the waveguides. It is discussed in chapter 7. A reader should be careful in the dual use of terminology TE/TM to show the mode of propagation , and also the polarization of propagation . For the guided waves, TE/TM is modes of propagation; and in the open medium, it indicates the polarization of the propagating waves. The second use in the context of obliquely incident EM‐waves at the interface of two medias is further discussed in section (5.2)of chapter 5.
On solving the above wave equations, the time‐harmonic wave propagating in the positive x‐direction is obtained as,
(4.7.6) 
In the above equations, k 0and c are wavenumber and velocity of EM‐waves in free space. Also, k eand k oare wavenumbers of the extraordinary waves and ordinary waves, respectively, traveling in the x‐direction with phase velocities v peand v po. The extraordinary waves are y‐polarized, i.e. TE‐polarized wave viewing the permittivity component ε r‖. The ordinary waves are z‐polarized, i.e. TM‐polarized wave viewing the permittivity component ε r⊥. Thus, an obliquely incident linearly polarized EM‐waves, with E yand E zcomponents, entering the slab of the anisotropic medium is split into two distinct normal mode waves and travel with two different phase velocities. They come out from the slab with a phase difference. This phenomenon is known as double refraction or birefringence . The dispersion relation for both normal waves is discussed in sub section (4.7.5).
The wave impedances η eand η oof the extraordinary waves and ordinary waves propagating in the x‐direction are obtained by substituting the field solutions of equation (4.7.6)in equations (4.7.3)and (4.7.4):
(4.7.7) 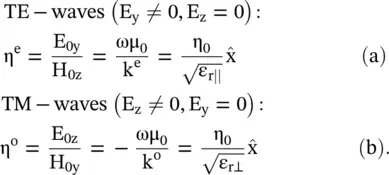
The plasma medium could be taken as an example. It is a uniaxial anisotropic medium with ε r⊥= 1 and ε r‖= ε r. In this case, y‐polarized extraordinary waves travel with a slower phase velocity v peas compared to a phase velocity v poof the z‐polarized ordinary waves. So, the extraordinary waves are also known as the slow‐waves with ε r‖> ε r⊥. The ordinary waves are called fast‐waves . The optic axis of the uniaxial medium is called the slow‐wave axis and ordinary axis as the fast‐wave axis .
Waveplates and Phase Shifters
The incident linearly polarized wave on a slab at 45° has two in‐phase E‐field components. After traveling a distance d, the field components develop a phase difference Δφ. So, for the case E oy= E oz= E 0and a phase difference Δφ = 90° at the output of the slab of thickness x = d, the uniaxial anisotropic dielectric slab converts linearly polarized incident waves into the circularly polarized waves. It is shown below:
(4.7.8) 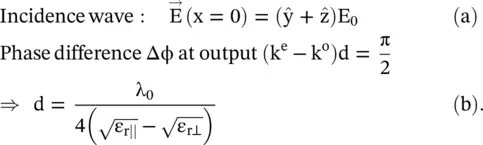
The electric components of the extraordinary and ordinary waves and also the total E‐field at the output of the slab are
(4.7.9) 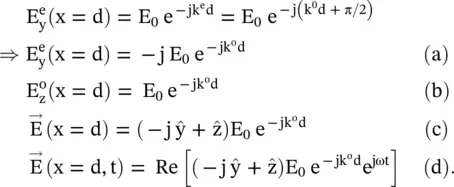
The wave at the output of the slab is a left‐hand circularly polarized wave. Such a slab converting the incoming linearly polarized wave to the circularly polarized waves is called the quarter‐waveplate . A waveplate with 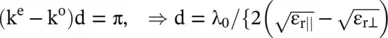 , i.e. the half‐waveplate rotates the 45° linearly polarized waves by 90° and output electric field component is
, i.e. the half‐waveplate rotates the 45° linearly polarized waves by 90° and output electric field component is 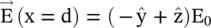 . The phase of the outgoing waves could be controlled by changing the thickness of a slab. The waveplate acts as a phase shifter . In the case of uniaxial anisotropic plasma medium, the permittivity components are ε r‖= ε rand ε r⊥= 1.
. The phase of the outgoing waves could be controlled by changing the thickness of a slab. The waveplate acts as a phase shifter . In the case of uniaxial anisotropic plasma medium, the permittivity components are ε r‖= ε rand ε r⊥= 1.
The above characteristics of a slab are also realized by thin metasurfaces discussed in subsections (22.5) and (22.6) of chapter 22.
4.7.2 Wave Propagation in Uniaxial Gyroelectric Medium
Figure (4.13b)shows uniform TEM‐waves propagation in the z‐direction in an unbounded uniaxial gyroelectric medium created by the magnetized plasma on the application of the DC magnetic field H 0in the z‐direction. The permittivity tensor [ε r] of the medium is given equation (4.2.11). Due to the presence of off‐diagonal matrix elements ±jκ in the permittivity matrix of the gyroelectric medium, the E xcomponent of the linearly polarized incident wave also generates the E ycomponent with a time quadrature. It is due to the presence of factor “j.” Similarly, the E ycomponent of an incident wave generates E xcomponent also with a time quadrature. The presence of two orthogonal E‐field components with a time quadrature in a gyroelectric medium creates the left‐hand circularly polarized (LHCP) and right‐hand circularly polarized (RHCP) waves as the normal modes in the uniaxial gyroelectric medium. Both circularly polarized waves travel with two different phase velocities. Thus, the gyro medium with the cross‐coupling gyrotropic factor ±jκ has the ability of polarization conversion.
Maxwell equation (4.7.2a)is expanded in the usual way to get the transverse field components E x, E yand H x, H y:
(4.7.10) 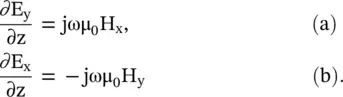
However, the Maxwell equation (4.7.2b)in the present case is expanded differently:
(4.7.11) 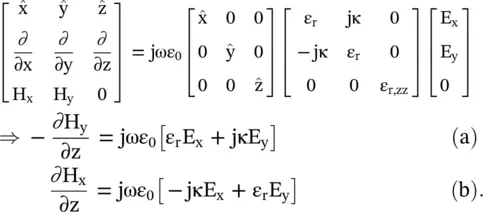
Читать дальше

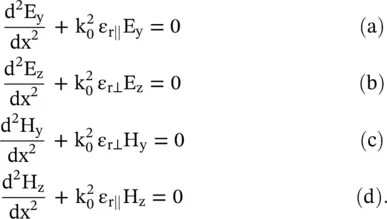
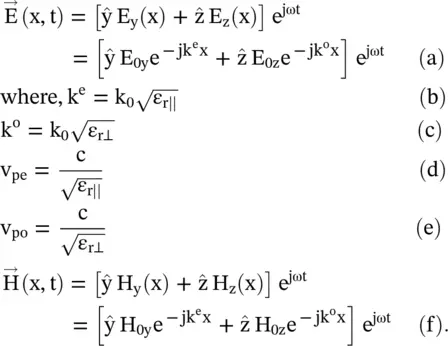
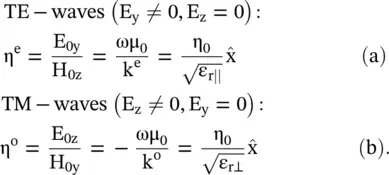
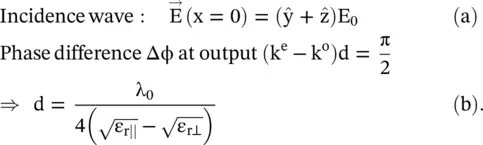
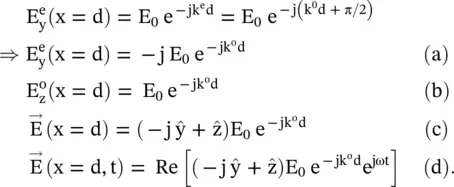
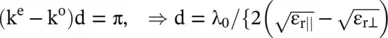 , i.e. the half‐waveplate rotates the 45° linearly polarized waves by 90° and output electric field component is
, i.e. the half‐waveplate rotates the 45° linearly polarized waves by 90° and output electric field component is 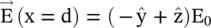 . The phase of the outgoing waves could be controlled by changing the thickness of a slab. The waveplate acts as a phase shifter . In the case of uniaxial anisotropic plasma medium, the permittivity components are ε r‖= ε rand ε r⊥= 1.
. The phase of the outgoing waves could be controlled by changing the thickness of a slab. The waveplate acts as a phase shifter . In the case of uniaxial anisotropic plasma medium, the permittivity components are ε r‖= ε rand ε r⊥= 1.