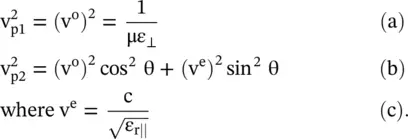The 2D dispersion diagram of both the ordinary and extraordinary waves is considered in the (y‐z)‐plane with the help of equations (4.7.26c)and (4.7.26d). Equation (4.7.26c)is the equation of an isofrequency dispersion circle, shown in Fig. (4.15a)in the (k y‐k z) plane. It is the dispersion relation of the ordinary waves in the isotropic (y‐z)‐ plane. The wavenumber 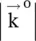 of the ordinary wave is independent of permittivity ε ‖along the z‐axis.
of the ordinary wave is independent of permittivity ε ‖along the z‐axis.
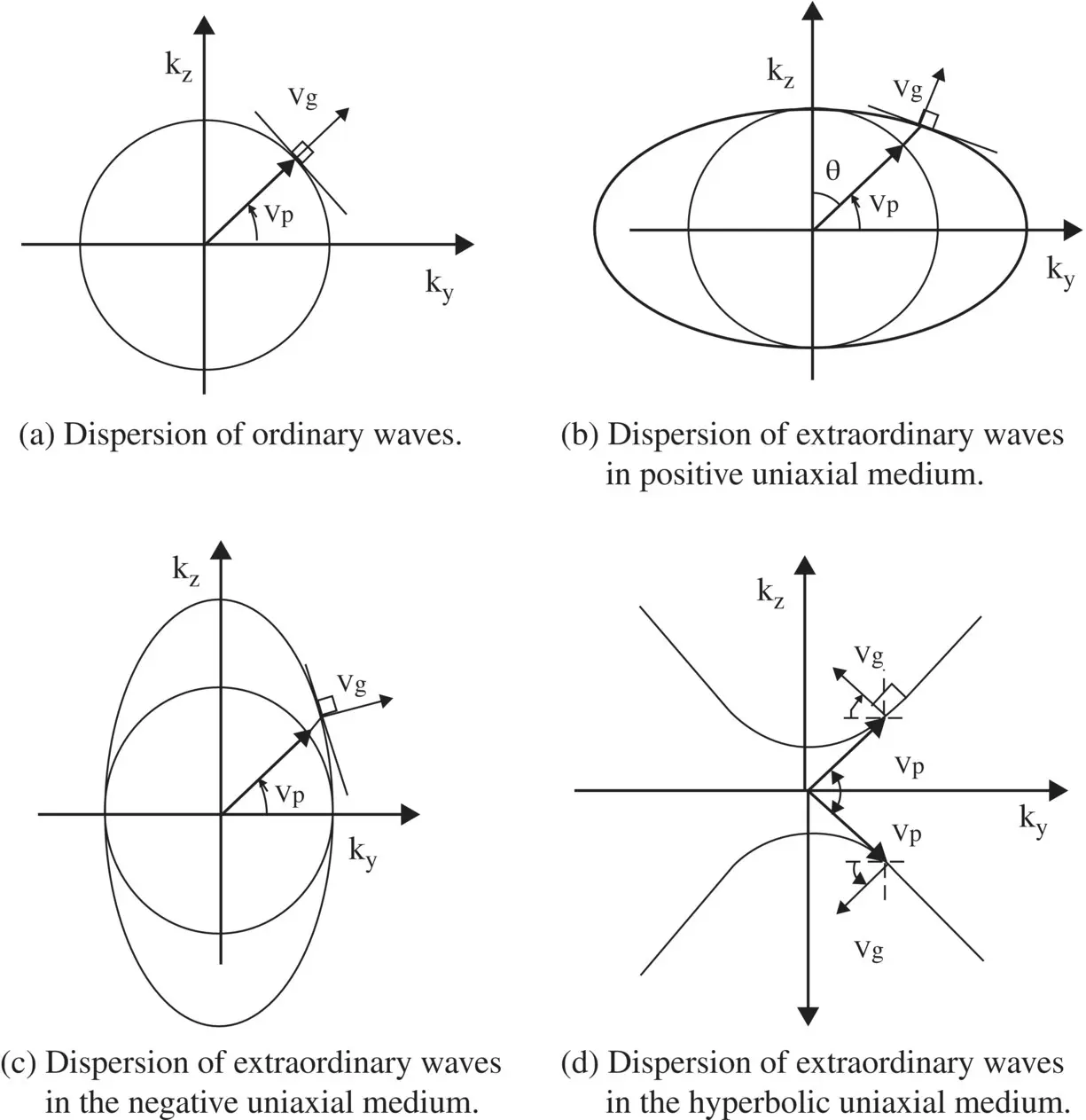
Figure 4.15 Dispersion diagrams in the uniaxial anisotropic medium.
Likewise, equation (4.7.26d)is the dispersion relation of the extraordinary waves, giving the isofrequency ellipse in the (k y‐k z)‐plane, as shown in Fig. (4.15b). In this case, the wavenumber is direction‐dependent because the relative permittivity for this case is direction‐dependent, 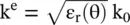 . The wavevector k esubtends an angle θ with respect to the z‐optic axis. In this case, wavevectors components are
. The wavevector k esubtends an angle θ with respect to the z‐optic axis. In this case, wavevectors components are 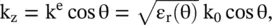 and
and 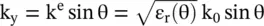 . Using, these relations with equation (4.7.26d), the following equation of ellipse of permittivity, supporting the extraordinary wave, is obtained:
. Using, these relations with equation (4.7.26d), the following equation of ellipse of permittivity, supporting the extraordinary wave, is obtained:
(4.7.27) 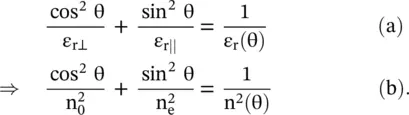
The dispersion relation (4.7.27b)is in the term of refractive indices. The refractive index n(θ) is the direction‐dependent, and n 0and n eare refractive indices for the ordinary and extraordinary waves. The wave analysis using the refractive index, in place of permittivity and permeability, is commonly used for the optical wave propagation in the uniaxial medium [B.18–B.20].
Figure (4.15a)shows that the ordinary waves have both the phase and group velocities, on the isofrequency contour, in the same direction. Figure (4.15b)shows the elliptical dispersion diagram for the extraordinary waves. In this case, there is a deviation of the direction of the group velocity from the direction of the phase velocity. The inner circle of Fig. (4.15b)shows the dispersion diagram of the ordinary waves with relative permittivity 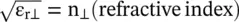 . Along the k y,the extraordinary waves have relative permittivity
. Along the k y,the extraordinary waves have relative permittivity 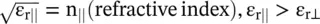 . Only along the z‐optic axis, i.e. along the k z‐axis, the identical relative permittivity for both kinds of waves is obtained. In all other directions, the ordinary wave is a fast‐wave as compared to the extraordinary wave. The medium is known as the positive uniaxial medium . Figure (4.15c)shows the case of the negative uniaxial medium . In this case, ε r‖< ε r⊥and the ordinary wave is a slow‐wave as compared to the extraordinary wave in all directions except along the y‐axis.
. Only along the z‐optic axis, i.e. along the k z‐axis, the identical relative permittivity for both kinds of waves is obtained. In all other directions, the ordinary wave is a fast‐wave as compared to the extraordinary wave. The medium is known as the positive uniaxial medium . Figure (4.15c)shows the case of the negative uniaxial medium . In this case, ε r‖< ε r⊥and the ordinary wave is a slow‐wave as compared to the extraordinary wave in all directions except along the y‐axis.
The phase velocities v p1and v p2of the ordinary and extraordinary waves using equations (4.7.26a)and (4.7.27a)are expressed through the following relations [B.3]:
(4.7.28) 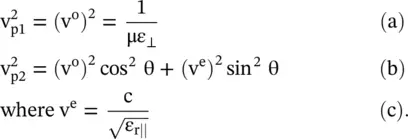
The phase velocity v p1of the ordinary wave is independent of the angle θ. However, the phase velocity v p2of the extraordinary wave is dependent on the angle θ. In Figure (4.15b), both velocities are identical only for the wave propagation along the z‐optic axis.
Finally, it is possible to artificially realize a uniaxial anisotropic material with one of the permittivity components as a negative quantity, say ε r⊥= − |ε r⊥|. In this case, equation (4.7.26d)shows the hyperbolic dispersion relation. This medium is known as the hypermedium . It supports the wave propagation with a larger value of wavenumbers and can convert an incident evanescent wave to the propagating waves. Such engineered materials are needed by the hyperlens [J.1, J.7]. Figure (4.15d)shows the dispersion relation of the hypermedium with phase and group velocities. In this case, y‐components of v pand v gare opposite to each other. So, the hypermedium supports the backward wave propagation, and it is a metamaterial medium. The hyperlens is discussed in the subsection ( 5.5.6) of chapter 5.
1 B.1 Baden‐Fuller, A.J.: Microwaves, 3rd Edition, Pergamon Press, New York, 1990.
2 B.2 Jordan, E.C.; Balmain Keith, G.E.: Electromagnetic Wave and Radiating System, Prentice‐Hall India, New Delhi, 1989.
3 B.3 Ramo, S.; Whinnery, J.R.; Van Duzer, T.: Fields, and Waves in Communication Electronics, 3rd Edition, John Wiley & Sons, Singapore, 1994.
4 B.4 Collin, R.E.: Foundations for Microwave Engineering, 2nd Edition, McGraw‐Hill, Inc., New York, 1992.
5 B.5 Rao, N.N.: Elements of Engineering Electromagnetics, 3rd Edition, Prentice‐Hall, Englewood Cliff, NJ, 1991.
6 B.6 Sadiku, M.N.O.: Elements of Electromagnetics, 3rd Edition, Oxford University Press, New York, 2001.
7 B.7 Cheng, D.K.: Fields and Wave Electromagnetics, 2nd Edition, Pearson Education, Singapore, 1989.
8 B.8 Weeks, W.L.: Electromagnetic Theory for Engineering Applications, John Wiley & Sons, New York, 1964.
9 B.9 Balanis, C.A.: Advanced Engineering Electromagnetics, John Wiley & Sons, New York, 1989.
10 B.10 Hipple, A. Von: Dielectrics, and Waves, Artech House, Norwood, MA, 1995.
11 B.11 Plonsey, R.; Collin, R.E.: Principle and Applications of Electromagnetic Fields, TMH, New Delhi, 1973.
12 B.12 Polivanov, K.: The Theory of Electromagnetic Fields, Mir Publisher, Moscow, 1975.
13 B.13 Orfanidis, S.J.: Electromagnetic Waves and Antenna, Free Book on the Web.
14 B.14 Staelin, D.H.; Morgenthaler, A.W.; Kong, J.A.: Electromagnetic Waves, Prentice‐Hall, Englewood Cliffs, NJ, 1994.
15 B.15 Landau, L.D.; Lifshitz, E.M.; Pitaevskii, L.P.: Electrodynamics of Continuous Media, Pergamon Press, New York, 1984.
16 B.16 Engheta, N.; Ziolkowski, R.W. (Editors): Metamaterials: Physics and Engineering Explorations, Wiley‐Interscience, John Wiley & Sons, Inc., Hoboken, NJ, 2006.
17 B.17 Lakhtakia, A.; Varadan, V.K.; Varadan, V.V.: Time‐Harmonic Electromagnetic Fields in Chiral Media, Springer‐Verlag, Berlin, Heidelberg, 1989.
18 B.18 Born, M.; Wolf, E.: Principles of Optics, 6th Edition, Pergamon Press, New York, 1980.
19 B.19 Haus, H.A.: Waves and Fields in Optoelectronics, Prentice‐Hall, Englewood Cliffs, NJ, 1984.
Читать дальше

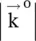 of the ordinary wave is independent of permittivity ε ‖along the z‐axis.
of the ordinary wave is independent of permittivity ε ‖along the z‐axis.
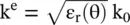 . The wavevector k esubtends an angle θ with respect to the z‐optic axis. In this case, wavevectors components are
. The wavevector k esubtends an angle θ with respect to the z‐optic axis. In this case, wavevectors components are 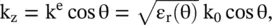 and
and 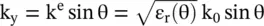 . Using, these relations with equation (4.7.26d), the following equation of ellipse of permittivity, supporting the extraordinary wave, is obtained:
. Using, these relations with equation (4.7.26d), the following equation of ellipse of permittivity, supporting the extraordinary wave, is obtained: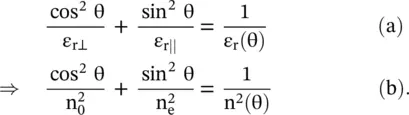
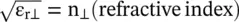 . Along the k y,the extraordinary waves have relative permittivity
. Along the k y,the extraordinary waves have relative permittivity 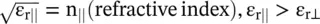 . Only along the z‐optic axis, i.e. along the k z‐axis, the identical relative permittivity for both kinds of waves is obtained. In all other directions, the ordinary wave is a fast‐wave as compared to the extraordinary wave. The medium is known as the positive uniaxial medium . Figure (4.15c)shows the case of the negative uniaxial medium . In this case, ε r‖< ε r⊥and the ordinary wave is a slow‐wave as compared to the extraordinary wave in all directions except along the y‐axis.
. Only along the z‐optic axis, i.e. along the k z‐axis, the identical relative permittivity for both kinds of waves is obtained. In all other directions, the ordinary wave is a fast‐wave as compared to the extraordinary wave. The medium is known as the positive uniaxial medium . Figure (4.15c)shows the case of the negative uniaxial medium . In this case, ε r‖< ε r⊥and the ordinary wave is a slow‐wave as compared to the extraordinary wave in all directions except along the y‐axis.