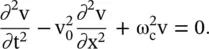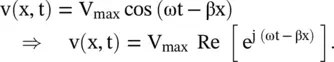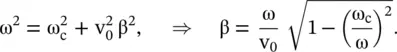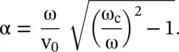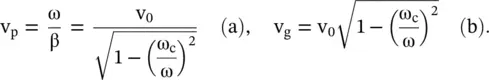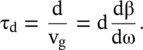(3.4.1) 
For the limiting case, Δx → 0, Δt → 0, the following expressions are obtained:
(3.4.2) 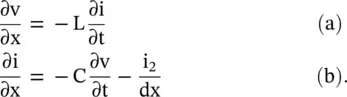
The voltage v across the shunt inductor is
(3.4.3) 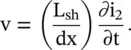
From equation (3.4.2a,b), the following voltage wave equation is obtained:
(3.4.4) 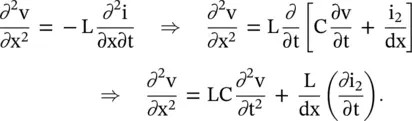
On substituting ∂ i 2/∂t from equation (3.4.3)in the above equation, the above wave equation is reduced to
(3.4.5) 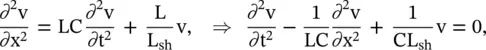
where 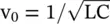 is the phase velocity of the standard nondispersive line without shunt loaded inductance, i.e. for the case L sh→ ∞. For a line in the air medium, the phase velocity is the velocity of the EM‐wave in a vacuum, i.e. v 0= c. The cut‐off frequency is defined as
is the phase velocity of the standard nondispersive line without shunt loaded inductance, i.e. for the case L sh→ ∞. For a line in the air medium, the phase velocity is the velocity of the EM‐wave in a vacuum, i.e. v 0= c. The cut‐off frequency is defined as 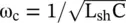 . Finally, the above voltage wave equation of the dispersive transmission line is rewritten as
. Finally, the above voltage wave equation of the dispersive transmission line is rewritten as
(3.4.6) 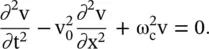
Equation (3.4.6)is known as the Klein–Gordon equation [B.20]. For a line without cut‐off frequency, i.e. for ω c= 0, the above equation is reduced to the standard dispersionless transmission line equation (2.1.24)of chapter 2. On assuming the harmonic solution for the forward‐moving voltage, the voltage on the loaded line is
(3.4.7) 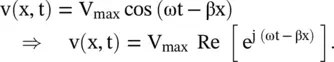
On substituting equation (3.4.7)in equation (3.4.6), the following dispersion relation is obtained:
(3.4.8) 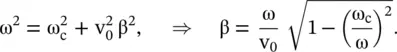
Equation (3.4.8)is identical to equation (3.3.8a)for the plasma medium. The cut‐off frequency ω cof the loaded line corresponds to the plasma frequency ω p. Thus, a plasma medium can be modeled by the shunt inductor loaded transmission line . Further, Fig (3.27a)shows that below the cut‐off frequency, i.e. for ω < ω cthe circuit is reduced to the L‐L circuit presenting inductors in both the series and shunt arm. Such a medium is called the epsilon negative (ENG) medium , discussed in section (5.5)of chapter 5.
For frequency ω < ω c, the propagation constant β is the imaginary quantity and the voltage wave cannot propagate on the shunt inductor loaded line. The voltage wave propagates only for ω > ω c. Thus, the shunt inductor loaded line behaves like a high‐pass filter (HPF). It is like a metallic waveguide discussed in subsection (7.4.1) of chapter 7. For ω < ω c, the loaded line supports the nonpropagating attenuated wave, called the evanescent wave . Its attenuation constant α is obtained by the following expression:
(3.4.9) 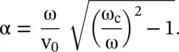
The phase and group velocities of the wave on the loaded dispersive line are
(3.4.10) 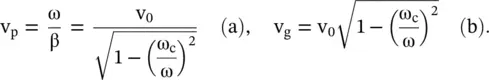
Figure (3.27b)shows the dispersion behavior, i.e. the function ω = f(β), on the (ω − β) diagram for the shunt inductor loaded line. It shows the frequency‐dependent behavior of the propagation constant β and attenuation constant α. The dashed line is the light line . Its slope ψ at the origin is the phase velocity of the EM‐wave in free space, i.e. v p= v 0= c. The propagation constant β exists above the light line only for ω > ω cand wave attenuation occurs for ω < ω c. At location P, the local slope ϕ provides the group velocity v g, whereas the slope ψ of the point P at the origin O provides the phase velocity v pof the propagating EM‐wave on the loaded transmission line.
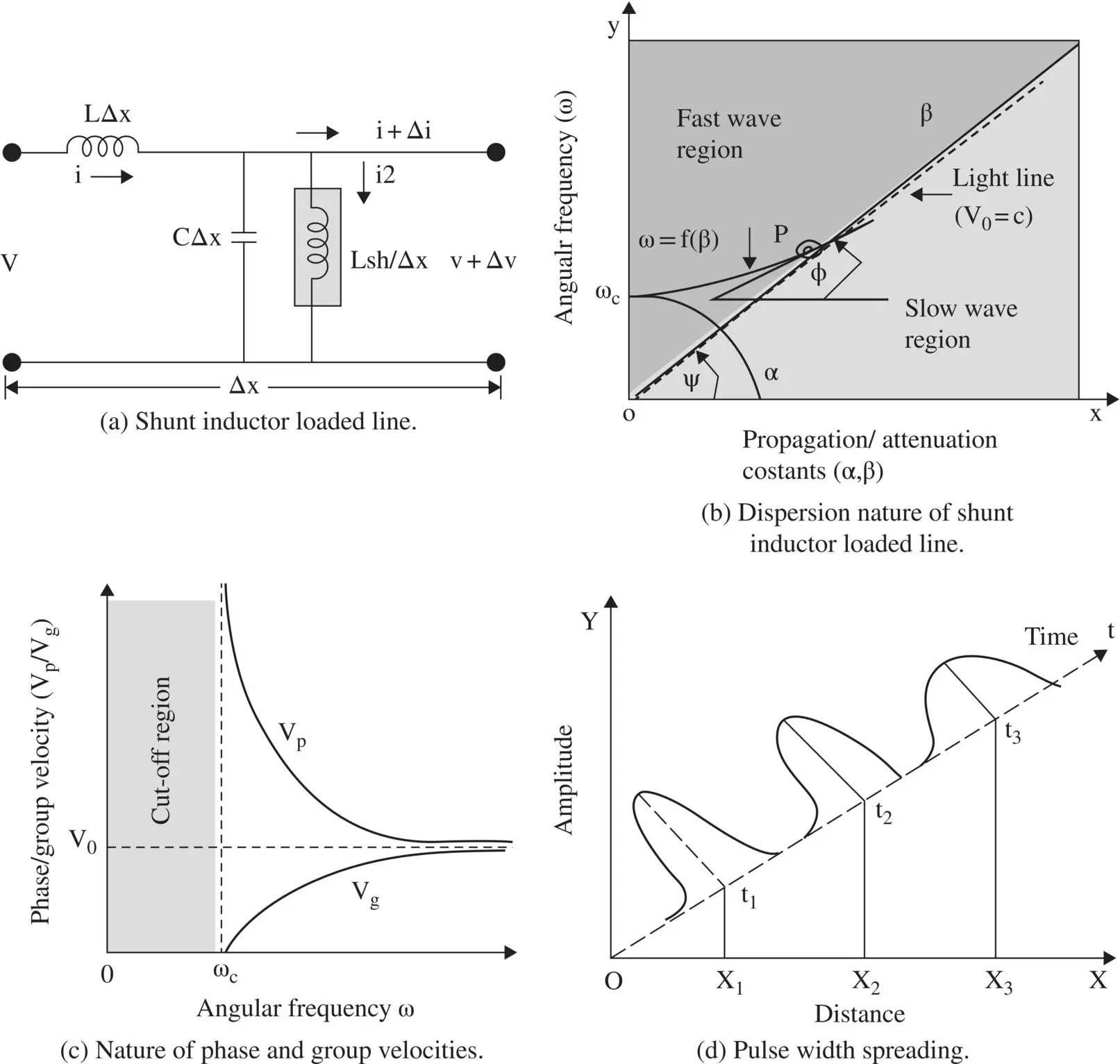
Figure 3.27 Shunt inductor loaded line and its characteristics.
Figure (3.27c)shows the variations in the phase velocity and the group velocity with frequency. For ω → ω c, v p→ ∞ , v g→ 0, and for ω → ∞, both wave velocities move toward the light line, i.e. toward the phase velocity (v 0) of the unloaded host transmission line. From equation (3.4.10a)dv p/dω is negative, i.e. the phase velocity decreases with frequency, whereas from the equation (3.4.10b), dv g/dω is positive, i.e. the group velocity increases with frequency. However, both velocities tend toward v 0, i.e. phase velocity in the unloaded host medium. Figure (3.27b)also shows that the propagation constant β increases with frequency. Thus, the shunt inductor loaded line has normal dispersion . The wave considered is a forward‐moving wave with both the phase and group velocities in the same direction, as both anti‐clockwise gradients ψ and ϕ defining the phase and group velocities respectively are positive. Above the cut‐off frequency, i.e. above the light line in the fast‐wave region, the phase velocity is higher than the phase velocity of the unloaded L‐C type transmission line. The shunt inductor loaded line supports the fast‐wave . The wave is fast as compared to the wave velocity, shown as the slope of the light line, on an unloaded transmission line.
The group velocity v gis also frequency‐dependent, causing dispersion in the envelope of a wave‐packet. Therefore, if a voltage wave‐packet, say a Gaussian wave‐packet, propagates on a shunt inductor loaded line, it disperses while moving forward. Figure (3.27d)shows that its amplitude decreases and the pulse width increases. This is known as the group dispersion . The time delay of the envelope over the distance d is
(3.4.11) 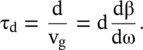
In the present subsection, the propagation constant of the loaded line is obtained by solving the wave equation. However, the dispersion relation and also the characteristics impedance of the loaded line could be obtained from the circuit analysis. This simple method is applicable to several interesting cases of loaded lines forming the basis for the modern Electromagnetic bandgap (EBG) materials and metamaterials.
Читать дальше


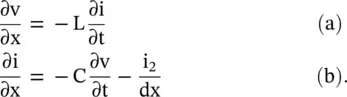
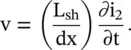
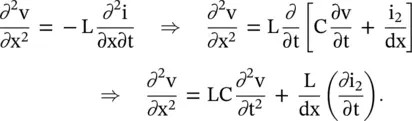
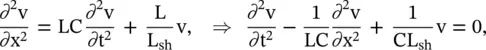
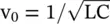 is the phase velocity of the standard nondispersive line without shunt loaded inductance, i.e. for the case L sh→ ∞. For a line in the air medium, the phase velocity is the velocity of the EM‐wave in a vacuum, i.e. v 0= c. The cut‐off frequency is defined as
is the phase velocity of the standard nondispersive line without shunt loaded inductance, i.e. for the case L sh→ ∞. For a line in the air medium, the phase velocity is the velocity of the EM‐wave in a vacuum, i.e. v 0= c. The cut‐off frequency is defined as 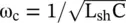 . Finally, the above voltage wave equation of the dispersive transmission line is rewritten as
. Finally, the above voltage wave equation of the dispersive transmission line is rewritten as