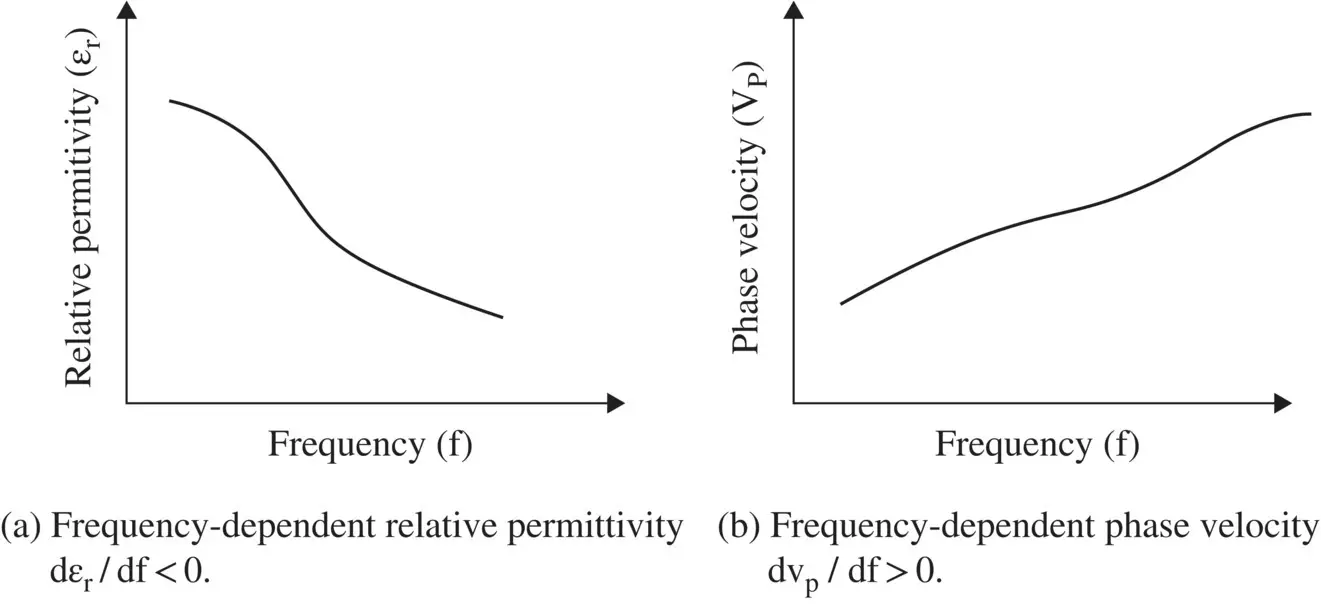
Figure 3.22 Nature of anomalous (negative) dispersion.
The concept of phase velocity applies to a single frequency signal. Now the question is to apply it to a complex baseband signal and a modulated signal. It is possible to use the phase velocity concept to such waveforms through the Fourier series of a periodic signal and using the Fourier integral for a nonperiodic signal. Any signal, periodic or nonperiodic, is composed of a large number of sinusoidal signals. They have a definite amplitude and phase relationship with the fundamental frequency of the signal. A combination of all sinusoidal components gives a complex signal of definite wave‐shape. If the complex waveshape travels through a dispersive medium having frequency‐dependent attenuation constant α(f), the amplitude of each signal component changes differently. Similarly, in a dispersive medium having a frequency‐dependent propagation constant β(f), each signal component travels with a different velocity. It results in different phase‐change for each frequency component of the complex wave; so the shape of the wave changes while traveling on a line or through the medium. The numerical inverse Fourier transform provides the wave‐shape of a signal in the time‐domain at any location in the medium. Thus, the Fourier method helps to apply the concept of phase velocity to complex waveform propagation [J.5, J.6]. Such investigations are important to maintain the signal integrity on the IC and MMIC chips.
A complex signal composed of two or more frequency components forms a wave‐packet . However, the frequency components should not be much different from each other like an amplitude modulated signal. Figure (3.23)shows the wave‐packet formed by a group of a narrowband complex signal. The wave‐packet has a central or a carrier frequency of higher value, superimposed with a low‐frequency envelope . The carrier wave travels with the phase velocity v p, whereas the envelope, i.e. the wave shape travels with the group velocity v g. In a nondispersive medium, the carrier wave and envelope both travel with the same velocity without a change in the waveshape. However, in the case of a dispersive medium, velocities of the carrier and envelope are different. Depending on the nature of dispersion, the wave could be the forward wave or the backward wave . If the medium has normal (positive) dispersion, the phase velocity, i.e. the velocity of the carrier wave, and the velocity of the envelope, i.e. the group velocity, are in the same direction, as shown in Fig (3.23). The wave is known as the forward wave. However, in the case of a highly anomalous (negative) dispersive medium, under a certain condition, the phase and group velocities are in the opposite directions, forming the backward wave.
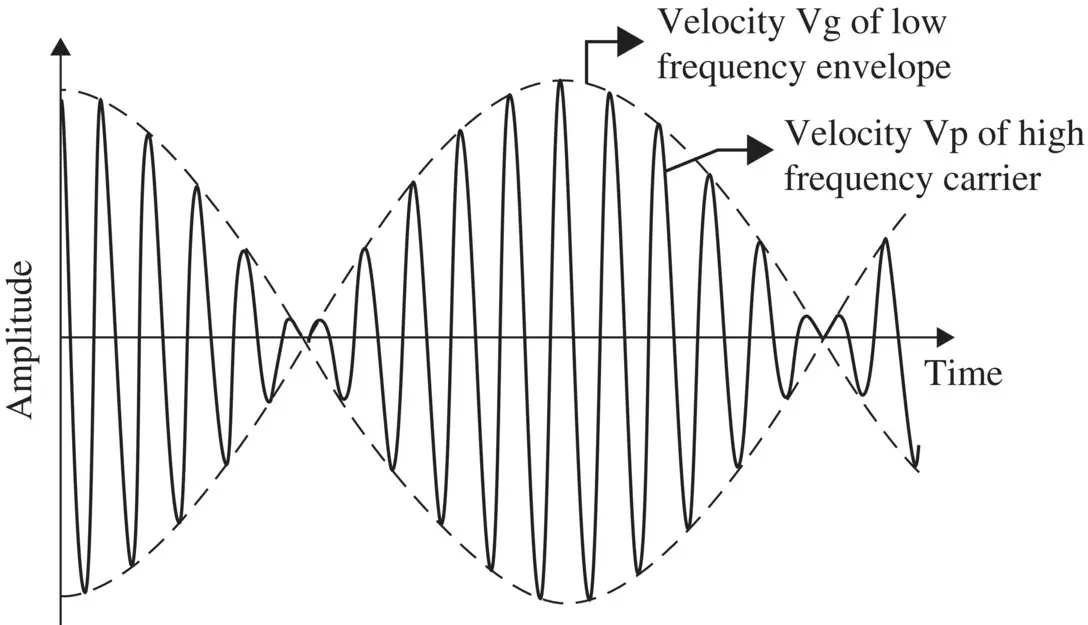
Figure 3.23 Description of phase and group velocities of a forward‐moving modulated wave.
The carrier and envelope are combined to form a unified wave structure called the wave‐packet. In the case of normal dispersion, the group velocity is the energy velocity of a signal and the information travels with the group velocity [B.1, B.4, B.5, B.7, B.14, B.16]. However, in the case of anomalous dispersion, the energy velocity and group velocity are different. In this case, group velocity is not velocity of information. Moreover, the concept of group velocity applies only to a narrow‐band wave‐packet, not to the wideband signal. The controversy exists at present on the travel of information with a velocity more than the velocity of light [J.7].
Formation of Two‐Frequency Wave‐Packet
A wave‐packet is formed by a linear combination of two signals of equal magnitude with a small difference in angular frequency and phase constant. It is shown in Fig (3.24). The composite voltage wave is given by
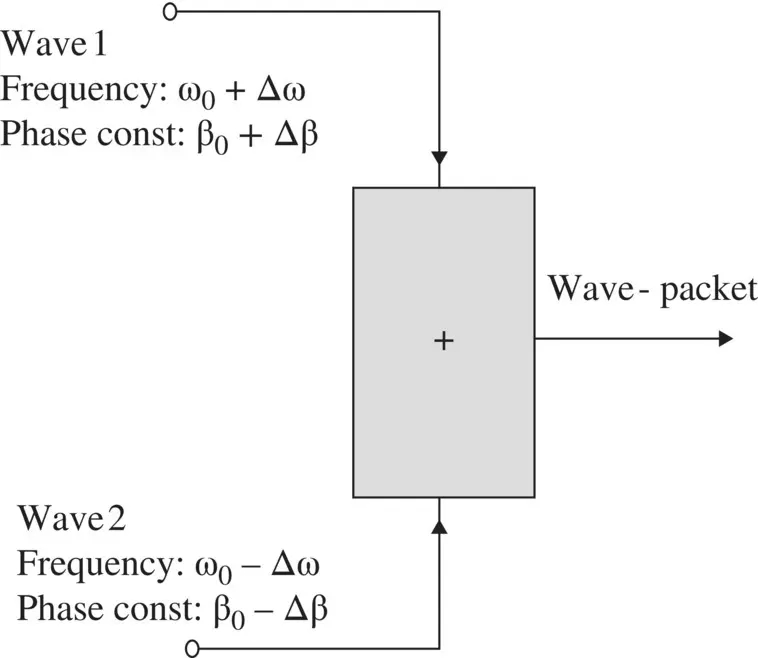
Figure 3.24 Formation of a wave‐packet.
(3.3.9) 
The carrier wave has frequency ω 0and propagation constant β 0. The above expression applies to a narrow‐band signal, Δω << ω 0. The envelope frequency is Δω and its propagation constant is Δβ. The carrier wave inside the envelope, shown in Fig (3.23), moves with phase velocity:
(3.3.10) 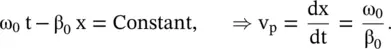
The velocity of the envelope, i.e. the group velocity, is obtained from the constant phase point on the envelope
(3.3.11) 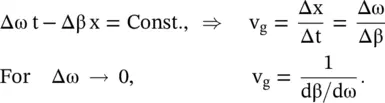
Both the phase velocity and group velocity are represented over the (ω − β) dispersion diagram of the wave‐supporting medium. The (ω − β) diagram plays a very significant role in the wave propagation in periodic and metamaterial media. These are discussed in the chapters 18– 22. Figure (3.25)shows the dispersion relation given by equation (3.3.8a). The point P on the dispersion diagram locates ( β 0, ω 0) . The slope ψ of a point P on the dispersion diagram, with respect to the origin, gives the phase velocity of a carrier wave, whereas the local slope ϕ at ω = ω 0, i.e. a local tangent at point P, provides the group velocity:
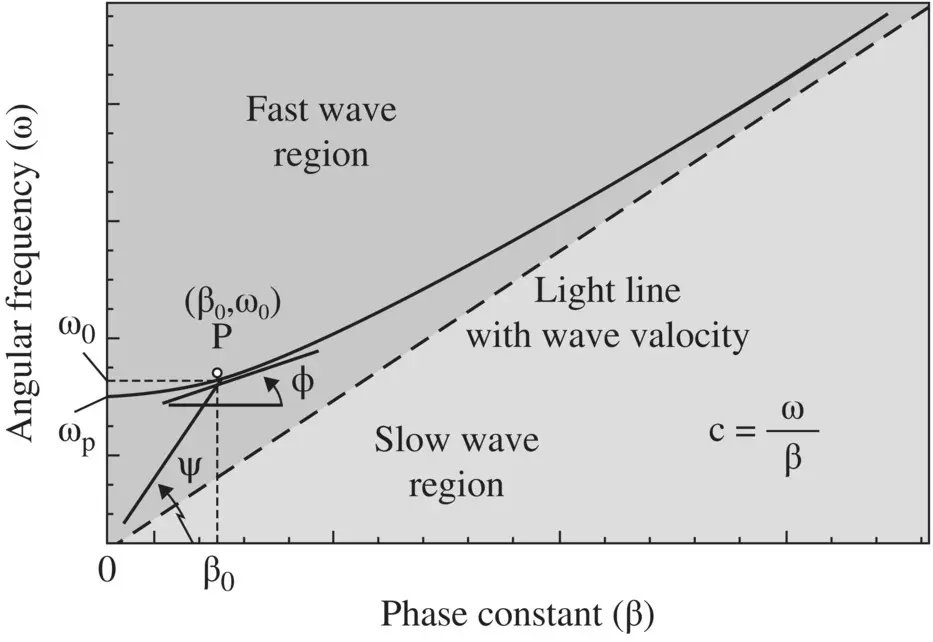
Figure 3.25 ω − β diagram to get phase and group velocities.
(3.3.12) 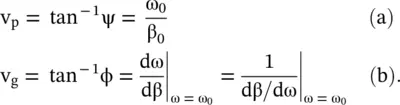
At the cut‐off frequency ω p, β → 0, results in an infinite extent of the phase velocity, while the group velocity is zero, v g= 0. However, away from the cut‐off frequency, the phase velocity decreases to a limiting value 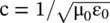 . It is the slope of the light–line as shown in Fig (3.25). The light‐line divides the (ω − β) diagram into two regions – within the light‐cone it is the fast‐wave region, and outside the light‐cone, it is the slow‐wave region. At much higher frequency, both velocities become equal. For the plasma medium, equations (3.3.8a)and (3.3.8b)provide the propagation constant and phase velocity.
. It is the slope of the light–line as shown in Fig (3.25). The light‐line divides the (ω − β) diagram into two regions – within the light‐cone it is the fast‐wave region, and outside the light‐cone, it is the slow‐wave region. At much higher frequency, both velocities become equal. For the plasma medium, equations (3.3.8a)and (3.3.8b)provide the propagation constant and phase velocity.
As the propagation constant increases from β = 0 at ω pto 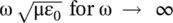 , and the phase velocity decreases from v p≈ ∞ at ω pto
, and the phase velocity decreases from v p≈ ∞ at ω pto 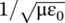 for ω → ∞, the plasma forms a normal, i.e. the positive dispersive medium. However, the phase velocity above the cut‐off frequency in a plasma medium is always greater than the velocity of EM‐wave in the free space, v p≥ c. This wave is a fast‐wave . The group velocity is computed as follows:
for ω → ∞, the plasma forms a normal, i.e. the positive dispersive medium. However, the phase velocity above the cut‐off frequency in a plasma medium is always greater than the velocity of EM‐wave in the free space, v p≥ c. This wave is a fast‐wave . The group velocity is computed as follows:
Читать дальше





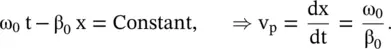
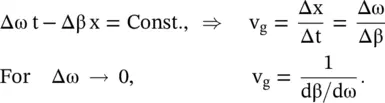

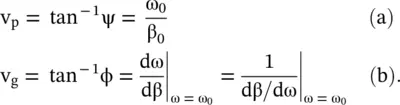
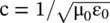 . It is the slope of the light–line as shown in Fig (3.25). The light‐line divides the (ω − β) diagram into two regions – within the light‐cone it is the fast‐wave region, and outside the light‐cone, it is the slow‐wave region. At much higher frequency, both velocities become equal. For the plasma medium, equations (3.3.8a)and (3.3.8b)provide the propagation constant and phase velocity.
. It is the slope of the light–line as shown in Fig (3.25). The light‐line divides the (ω − β) diagram into two regions – within the light‐cone it is the fast‐wave region, and outside the light‐cone, it is the slow‐wave region. At much higher frequency, both velocities become equal. For the plasma medium, equations (3.3.8a)and (3.3.8b)provide the propagation constant and phase velocity.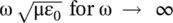 , and the phase velocity decreases from v p≈ ∞ at ω pto
, and the phase velocity decreases from v p≈ ∞ at ω pto 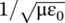 for ω → ∞, the plasma forms a normal, i.e. the positive dispersive medium. However, the phase velocity above the cut‐off frequency in a plasma medium is always greater than the velocity of EM‐wave in the free space, v p≥ c. This wave is a fast‐wave . The group velocity is computed as follows:
for ω → ∞, the plasma forms a normal, i.e. the positive dispersive medium. However, the phase velocity above the cut‐off frequency in a plasma medium is always greater than the velocity of EM‐wave in the free space, v p≥ c. This wave is a fast‐wave . The group velocity is computed as follows:










