(3.3.3) 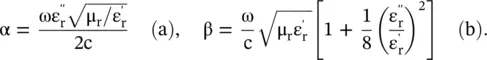
In equation (3.3.3), c is the velocity of EM‐wave in free space. The above expressions are obtained from equations ( 4.5.16) and ( 4.5.19) of chapter 4. The complex permittivity is given by ε = ε ′− jε ″. The imaginary part, showing a loss in a medium, is related to the conductivity of a medium through relation σ = ωε ″. If ε ′and ε ″are not frequency‐dependent, the propagation constant β is not frequency‐dependent and the phase velocity is also not frequency‐dependent. However, if they are frequency dependent, the phase velocity is also frequency‐dependent. The phase velocity in the low‐loss dielectric medium is
(3.3.4) 
Therefore, the presence of loss decreases the phase velocity of EM‐wave. This kind of wave is known as the slow‐wave . The slow‐wave can be dispersive or nondispersive. However, it is associated with a loss. This aspect is further illustrated through the EM‐wave propagation in a high conductivity medium. The conducting medium is discussed in subsection ( 4.5.5) of chapter 4. The attenuation (α), phase constant (β), and phase velocity (v p,con) of a highly conducting medium are given by equation ( 4.5.35b)of chapter 4[B.3]:
(3.3.5) 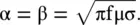
(3.3.6) 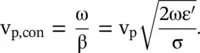
The above expressions are obtained for a highly conducting medium, σ/ωε >> 1. It does not apply to the lossless medium with σ = 0. The wave propagation is associated with significant loss (α) given by equation (3.3.5). Moreover, both the attenuation constant and phase velocity are frequency dependent, so a conducting medium is highly dispersive. However, the periodic structures and other mechanisms give slow‐wave structures with a small loss. Such structures are useful for the development of compact microwave components and devices [B.1, ]. The slow‐wave periodic transmission line structures are discussed in chapter 19.
Some EM‐wave supporting media have cut‐off property. They support the wave propagation only above the certain characteristic frequency of a medium or a structure. These media and structures are also dispersive. For instance, the nonmagnetic plasma medium has such cut‐off property [B.4, B.14]. The plasma medium is discussed in the subsection (6.5.2) of chapter 6. The permittivity of a plasma medium is given by equation (6.5.16 ):
(3.3.7) 
In the above expression, f pis the plasma frequency that is a characteristic cut‐off frequency of the plasma medium [B.4, B.14]. The permeability of nonmagnetized plasma is μ = μ 0. Other parameters are as follows‐ε 0: permittivity of free space, N: electron density, e: electron charge, and m e: electron mass. The propagation constant, phase velocity, and plasma wavelength λ plasmaof the EM‐wave wave in a plasma medium are given below:
(3.3.8) 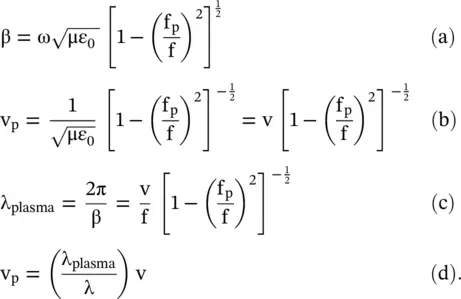
In equation (3.3.8), 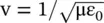 is the velocity of EM‐wave in the homogeneous medium with parameters ε 0and μ. The wavelength in the homogeneous medium is λ = v/f. However, the nonmagnetized plasma medium has the parameters ε 0, μ osupporting the wavelength λ 0= c/f. The nonmagnetized plasma medium behaves as free space.
is the velocity of EM‐wave in the homogeneous medium with parameters ε 0and μ. The wavelength in the homogeneous medium is λ = v/f. However, the nonmagnetized plasma medium has the parameters ε 0, μ osupporting the wavelength λ 0= c/f. The nonmagnetized plasma medium behaves as free space.
The phase velocity of the EM‐waves in a plasma medium is frequency‐dependent. Therefore, it is a dispersive medium that supports a fast‐wave . It is fast in the sense that the phase velocity is higher than the phase velocity of the EM‐wave in free space given by 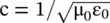 . The plasma medium exhibits the cut‐off phenomenon, similar to the cut‐off behavior of the waveguide medium. The waveguide medium is discussed in the section (7.4) of chapter 7. There is no wave propagation at the plasma frequency f = f p. The plasma frequency f pbehaves like the cut‐off frequency f cof a waveguide. Thus, the waveguide can be used to simulate the electrical behavior of plasma . For f < f p, no wave propagation takes place, as the propagation constant β becomes an imaginary quantity. Such a wave is known as an evanescent wave . It is an exponentially decaying nonpropagating wave (E = E 0e −αz). The standard metallic waveguide also supports the cut‐off phenomenon and has a frequency‐dependent phase velocity [B.1, B.5, B.7, B.8, B.15–B.17].
. The plasma medium exhibits the cut‐off phenomenon, similar to the cut‐off behavior of the waveguide medium. The waveguide medium is discussed in the section (7.4) of chapter 7. There is no wave propagation at the plasma frequency f = f p. The plasma frequency f pbehaves like the cut‐off frequency f cof a waveguide. Thus, the waveguide can be used to simulate the electrical behavior of plasma . For f < f p, no wave propagation takes place, as the propagation constant β becomes an imaginary quantity. Such a wave is known as an evanescent wave . It is an exponentially decaying nonpropagating wave (E = E 0e −αz). The standard metallic waveguide also supports the cut‐off phenomenon and has a frequency‐dependent phase velocity [B.1, B.5, B.7, B.8, B.15–B.17].
The dispersion is a property of the wave‐supporting medium. The phase velocity of a wave in a dispersive medium can either decrease or increase with the increase in frequency. Thus, all dispersive media could be put into two groups – (i) normal dispersive medium and (ii) abnormal or anomalous dispersive medium .
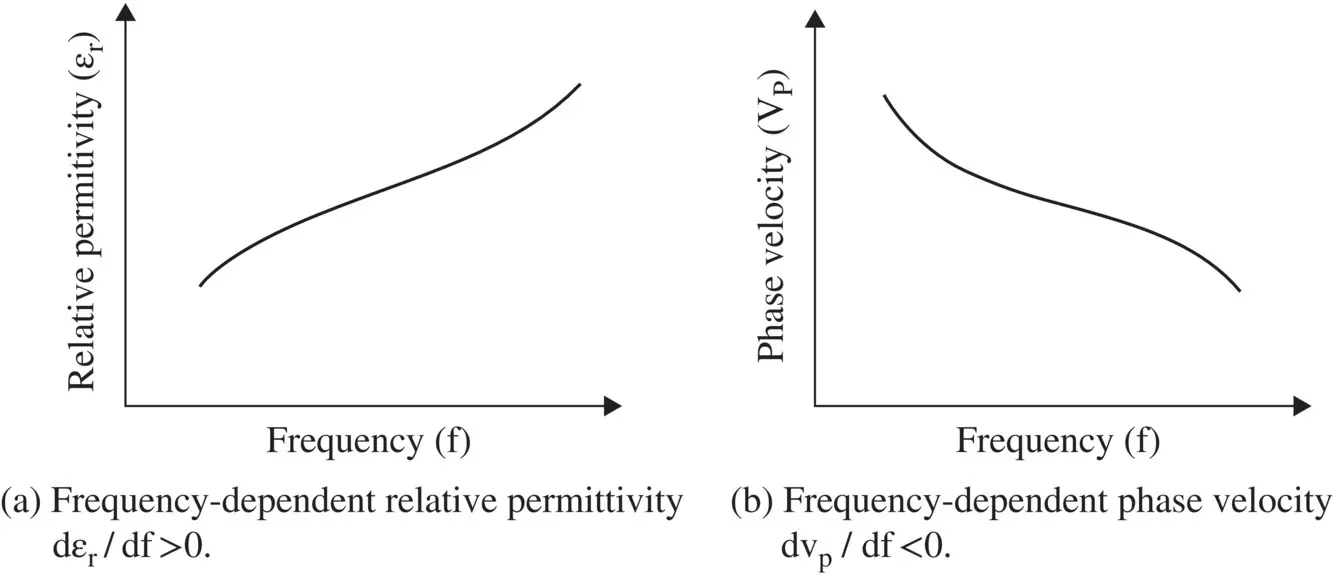
Figure 3.21 Nature of normal (positive) dispersion.
Figure (3.21a and b)show the general behavior of a medium having normal dispersion. The relative permittivity of such a medium increases with frequency, i.e. dε r/df is positive, and the phase velocity decreases with frequency, i.e. dv p/df is negative. A microstrip line provides such a medium for the normal dispersion. The effective relative permittivity of a microstrip line increases with frequency leading to a decrease in the phase velocity with an increase in frequency. The microstrip is discussed in chapter 8.
Figure (3.22a and b)show the general behavior of an anomalous dispersive medium. The relative permittivity of such a medium decreases with an increase in frequency, i.e. dε r/df < 0 (negative). It leads to an increase in the phase velocity with an increase in frequency, i.e. dv p/df > 0 (positive). A microstrip line on a semiconductor substrate having the Metal, Insulator, Semiconductor (MIS) or the Schottky structure, in the transition region, is an anomalous dispersive medium [J.3, J.4].
It is emphasized that there is nothing abnormal with the anomalous dispersion. Both kinds of dispersions exist in reality. The normal dispersion is also called the positive dispersion as the gradient of ε rwith frequency is positive, i.e. dε r/df > 0. Similarly, the anomalous dispersion is called the negative dispersion with dε r/df < 0. The relative permittivity of material undergoes both kinds of dispersion depending upon the physical cause of dispersion. The dispersion is caused by several kinds of material polarizations – dipolar, ionic, electronic, and interfacial polarization. Once the frequency is varied from low‐frequency to the optical frequency, the material medium undergoes these polarization changes, and the propagating wave experiences both the normal and anomalous dispersion at different frequencies [B.17, B.18]. It is discussed in chapter 6.
Читать дальше

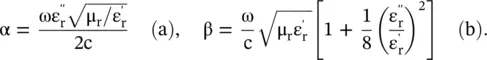

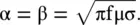
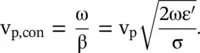

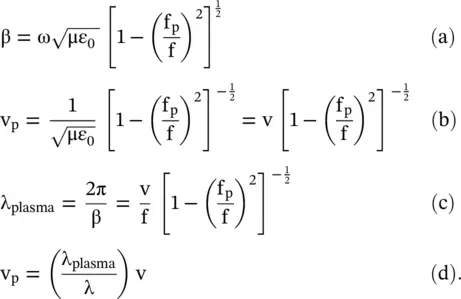
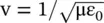 is the velocity of EM‐wave in the homogeneous medium with parameters ε 0and μ. The wavelength in the homogeneous medium is λ = v/f. However, the nonmagnetized plasma medium has the parameters ε 0, μ osupporting the wavelength λ 0= c/f. The nonmagnetized plasma medium behaves as free space.
is the velocity of EM‐wave in the homogeneous medium with parameters ε 0and μ. The wavelength in the homogeneous medium is λ = v/f. However, the nonmagnetized plasma medium has the parameters ε 0, μ osupporting the wavelength λ 0= c/f. The nonmagnetized plasma medium behaves as free space.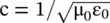 . The plasma medium exhibits the cut‐off phenomenon, similar to the cut‐off behavior of the waveguide medium. The waveguide medium is discussed in the section (7.4) of chapter 7. There is no wave propagation at the plasma frequency f = f p. The plasma frequency f pbehaves like the cut‐off frequency f cof a waveguide. Thus, the waveguide can be used to simulate the electrical behavior of plasma . For f < f p, no wave propagation takes place, as the propagation constant β becomes an imaginary quantity. Such a wave is known as an evanescent wave . It is an exponentially decaying nonpropagating wave (E = E 0e −αz). The standard metallic waveguide also supports the cut‐off phenomenon and has a frequency‐dependent phase velocity [B.1, B.5, B.7, B.8, B.15–B.17].
. The plasma medium exhibits the cut‐off phenomenon, similar to the cut‐off behavior of the waveguide medium. The waveguide medium is discussed in the section (7.4) of chapter 7. There is no wave propagation at the plasma frequency f = f p. The plasma frequency f pbehaves like the cut‐off frequency f cof a waveguide. Thus, the waveguide can be used to simulate the electrical behavior of plasma . For f < f p, no wave propagation takes place, as the propagation constant β becomes an imaginary quantity. Such a wave is known as an evanescent wave . It is an exponentially decaying nonpropagating wave (E = E 0e −αz). The standard metallic waveguide also supports the cut‐off phenomenon and has a frequency‐dependent phase velocity [B.1, B.5, B.7, B.8, B.15–B.17].











