Myron B. Allen, III - The Mathematics of Fluid Flow Through Porous Media

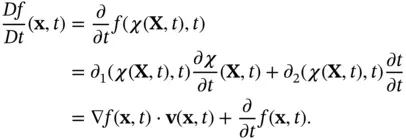
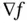In the third line of this derivation, denotes the gradient of the function 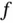, that is, its derivative with respect to the vector‐valued spatial position 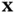. With respect to any orthonormal basis 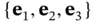, as drawn in Figure 2.4,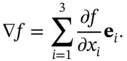

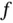In short, for a function of spatial position and time, the material derivative is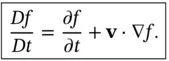

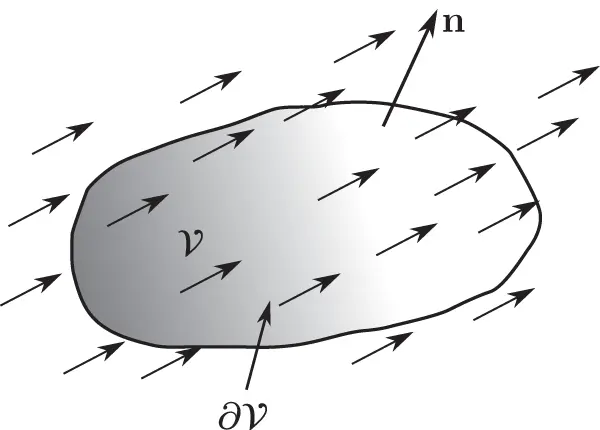
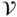The partial differential equations (PDEs) governing flows through porous media arise from balance laws. All of the flows treated in this book are isothermal, that is, the temperature is constant in time and uniform in space. With this assumption in place, we need only work with the balance laws governing mass and momentum—with one exception noted below.

Figure 2.5 A time‐independent region having oriented boundary 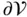and unit outward normal vector field 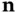. The small arrows represent the spatial velocity.

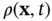Consider first the mass balance. We associate with each body a nonnegative, integrable function , called the mass density. This function gives the mass contained in any region 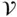of three‐dimensional Euclidean space as the volume integral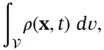

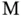(2.2)

having physical dimension . Here, 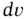denotes the element of volume integration. Since 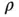is nonnegative, so is the mass. The expression (2.2)requires that .

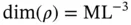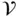The mass balance arises from a simple observation: The rate of change in the mass inside any region of three‐dimensional space exactly balances the rate of movement of mass across the region's boundary. In symbols,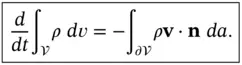

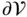(2.3)

This equation is the integral mass balance. Here, denotes the boundary of 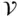; 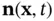denotes the unit‐length vector field orthogonal to 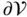and pointing outward, as Figure 2.5depicts; and 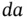denotes the element of surface integration. We call the function 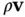in the integral on the right side of Eq. (2.3)the mass fluxper unit area; the integrand 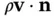is the component of mass flux per unit area in the direction of the unit vector 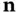, that is, outward from 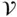. The surface integral itself, together with the negative sign, is the net fluxof mass inward across .

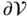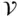Often of greater utility than the integral equation (2.3)is a pointwise form of the mass balance, valid when the density and velocity are sufficiently smooth. To derive this form, consider a region that does not change in time. In this case,

(2.4)

Also, by the divergence theorem,

(2.5)