Myron B. Allen, III - The Mathematics of Fluid Flow Through Porous Media

Figure 2.3 Regions and occupied by a body in two reference configurations, along with the corresponding deformations and 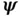that map a given particle onto a position vector 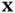at time .

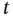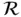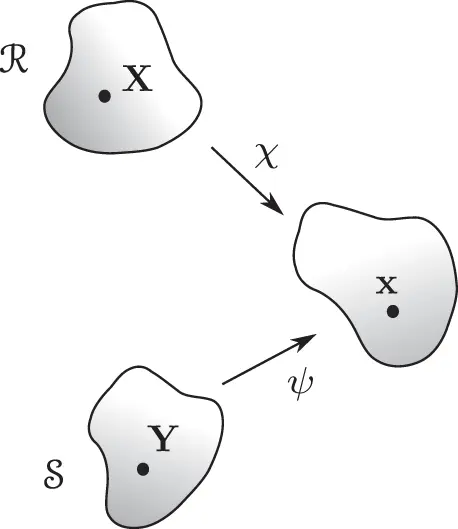
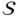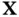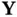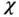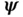Exercise 2.1 Let and be the regions occupied by a body in two different reference configurations, giving the referential coordinates of a certain particle as and , respectively, as illustrated in Figure 2.3. Let and , respectively, denote the deformations associated with these two reference configurations. Thus the spatial position of the particle at time 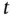is 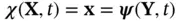. Justify the relationship 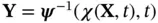. This relationship makes it possible to reconcile the analyses of motion by observers who choose different reference configurations .

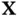In classical mechanics, it is straightforward to calculate a particle's velocity: Differentiate the particle's spatial position with respect to time. Continuum mechanics employs the same concept. The velocityof particle is the time derivative of its position: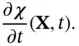

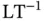(2.1)

This function has dimension . In taking this partial derivative, we hold the particle 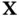fixed and differentiate with respect to 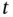, just as in classical mechanics. We call the velocity (2.1)the referential velocityor Lagrangian velocity.

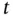We distinguish this velocity from another notion of velocity that arises by measuring what happens at a fixed position in space, as with an anemometer or wind vane attached to a stationary building. This concept of velocity commonly arises in fluid mechanics. In this case, we differentiate with respect to , holding the spatial coordinate 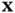fixed. To calculate this spatialor Eulerian velocityfrom the deformation, we first determine which particle 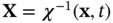passes through 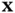at time 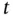, then compute the velocity of that particle: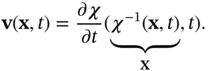

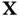Figure 2.4 Orthonormal basis vectors defining a Cartesian coordinate system.

Since the idea of differentiating with respect to time holding the particle fixed applies to other functions, we adopt a special notation for this operation, called the material derivative. If 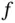is a differentiable function of 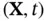—that is, a function of referential coordinates—its material derivative is straightforward: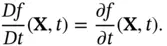

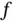However, if is a function of spatial coordinates 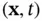, where 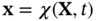, calculating its material derivative requires the chain rule. In this context, several common notations for partial differentiation can be ambiguous. If we denote by 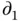and 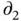the operations of partial differentiation of 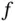with respect to its first and second arguments 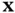and 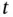, respectively, then