Interest in the mathematics of porous‐medium flows blossomed as oil production increased in economic importance during the early twentieth century. Prominent in the early petroleum engineering literature in this area are works by P.G. Nutting [110], Morris Muskat and his collaborators [104–107, 159, 160], and Miles C. Leverett and his collaborators [29, 95–97]. Between 1930 and 1960, mathematicians, groundwater hydrologists, petroleum engineers, and geoscientists made tremendous progress in understanding the PDEs that govern underground fluid flows.
Today, mathematical models of porous‐medium flow encompass linear and nonlinear PDEs of all major types, as well as systems involving PDEs having different types. The analysis of these equations and their numerical approximations requires an increasing level of mathematical and computational sophistication, and the models themselves have become essential design tools in the management of underground fluid resources.
From a philosophical perspective, credit for these advances belongs to scientists and engineers who clung tenaciously—often in the face of skepticism on the part of more “practically” oriented colleagues—to two premises. The first is that the key to effective modeling resides in careful mathematical reasoning. While this premise seems platitudinous, at any moment in history some practitioners believe that their science is too inherently messy to justify fastidious mathematics. On the contrary, the need for painstaking logical inferences from premises and hypotheses is arguably never greater than when the data are complicated, confusing, or hard to obtain.
The second premise is more subtle: In the absence of good data, sound mathematical models are essential. Far from outstripping the data, mathematical models tell us what data we really need. Moreover, they tell us what qualitative properties we can expect in predictions arising from a given input data set. They also reveal how properties of the data, such as its spatial variability and uncertainty, affect the models' predictive capabilities. If the required data cannot in principle be acquired, if the qualitative properties of the model conflict with the empirical evidence, or if the model cannot, in principle, provide stable predictions in the face of heterogeneity and uncertainty, then we must admit that our understanding is incomplete.
1.2 Partial Differential Equations (PDEs)
Most realistic models of fluid flows in porous media use PDEs, “the natural dialect of continuum science” [62], written at scales appropriate for bench‐ or field‐scale observations. In practical applications, these equations are complicated. They are posed on geometrically irregular, multidimensional domains; they often have highly variable coefficients; they can involve coupled systems of equations; in many applications they are nonlinear. For these reasons, we must often replace the exact PDEs by arithmetic approximations that one can solve using electronic machines.
The practical need for computational methods notwithstanding, a grasp of the analytic aspects of the PDEs remains an important asset for any porous‐medium modeler. What types of initial and boundary conditions yield well‐posed problems? Do the solutions obey a priori bounds based on the initial or boundary data? Do the numerical approximations respect these bounds? Does the PDE tend to smooth or preserve numerically problematic sharp fronts as time advances? Do shocks form from continuous initial data?
In the first half of the twentieth century, pioneering numerical analysts Richard Courant, Kurt Friedrichs, Hans Lewy, and John von Neumann—all immigrants to the United States—recognized that one cannot successfully “arithmetize analysis” [23] without understanding the differential equations. Designing stable, convergent, accurate, and efficient approximations to PDEs requires mathematical insight into the equations being approximated. A visionary 1947 consulting report [152] by von Neumann, developing the first petroleum reservoir simulator designed for a computer, illustrates this principle.
This book aims to promote this type of insight. We examine PDE‐based models of porous‐medium flows in geometries and settings simple enough to admit analysis without numerical approximations but realistic enough to reveal important structures.
From a mathematical perspective, the study of fluid flows in porous media offers fertile ground for inquiry into PDEs more generally. In particular, this book employs many broadly applicable concepts in the theory of PDEs, including:
1 Mass and momentum balance laws
2 Variational principles
3 Fundamental solutions
4 The principle of superposition
5 Similarity methods
6 Stability analysis
7 The method of characteristics and jump conditions.
Where possible, the narrative introduces these topics in the simplest possible settings before applying them to more complicated problems.
Topic 1, covered in Chapter 2, deserves comment. Few PDE texts at this level discuss balance laws in the detail pursued here. However, it is hard to build intuition about porous‐medium flows without knowing the principles from which they arise. The balance laws furnish those principles. On the other hand, a completely rigorous study of balance laws for fluids flowing in porous media would require a monograph‐length treatment in its own right. Chapter 2reflects an attempt to weigh the importance of fundamental principles against the need for a concise explanation of how the governing PDEs emerge from basic laws of physics. The references offer suggestions for deeper inquiry.
We frequently refer to PDEs according to a classification system inherited from the algebra of quadratic equations. The utility of this system becomes more apparent as one becomes more familiar with examples. For now, it suffices to review the system for second‐order PDEs in two independent variables having the form
(1.1) 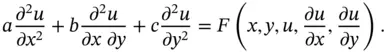
Here, 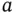 ,
, 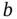 , and
, and 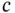 are functions of the independent variables
are functions of the independent variables 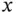 and
and 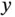 , which we can replace with
, which we can replace with 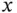 and
and 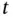 in time‐dependent problems;
in time‐dependent problems; 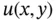 is the unknown solution; and
is the unknown solution; and 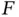 denotes a function of five variables that describes the lower‐order terms in the PDE.
denotes a function of five variables that describes the lower‐order terms in the PDE.
The highest-order terms determine the classification. The discriminantof Eq. (1.1)is 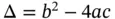 , which is a function of
, which is a function of 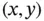 . Equation (1.1)is
. Equation (1.1)is
Читать дальше

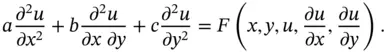
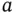 ,
, 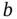 , and
, and 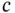 are functions of the independent variables
are functions of the independent variables 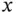 and
and 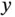 , which we can replace with
, which we can replace with 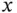 and
and 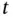 in time‐dependent problems;
in time‐dependent problems; 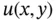 is the unknown solution; and
is the unknown solution; and 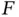 denotes a function of five variables that describes the lower‐order terms in the PDE.
denotes a function of five variables that describes the lower‐order terms in the PDE.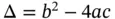 , which is a function of
, which is a function of 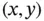 . Equation (1.1)is
. Equation (1.1)is










