Myron B. Allen, III - The Mathematics of Fluid Flow Through Porous Media

2 Chapter 3Figure 3.1 Schematic diagram of Darcy's apparatus for measuring water flow t...Figure 3.2 A piece of mathematical surface in a porous medium, in which shad...Figure 3.3 The transfer of momentum away from a solid object moving through ...Figure 3.4 Experimental configuration used to define 1 darcy.Figure 3.5 Schematic diagram of an array of fixed solid in which viscous eff...Figure 3.6 One‐dimensional flow geometry used to motivate the Forchheimer eq...Figure 3.7 Level sets of , 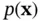shown as dashed curves, along with the gradient Figure 3.8 Construction of a scalar potential 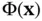such that , by computing a ...Figure 3.9 A piezometer showing the piezometric head 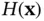as the height to whic...Figure 3.10 Geometry of areal flow in a confined aquifer. The elevations 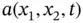a...Figure 3.11 Fluid flux across the upper confining layer.Figure 3.12 Sandstone core samples. Sample (a) has dark shale streaks parall...Figure 3.13 Direction cosine 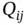between a vector 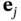in one orthonormal basis a...

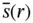3 Chapter 4Figure 4.1 Geometry of the Dupuit–Thiem model.Figure 4.2 Definition of the drawdown at an observation well.Figure 4.3 Calculation of transmissivity using drawdown data.Figure 4.4 A two‐dimensional region 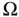with an external boundary 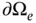and a well...Figure 4.5 Two‐dimensional region 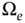used to model the region 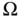in Figure 4.4...Figure 4.6 Graphs of the Theis solution for vertically averaged piezometric ...Figure 4.7 Hypothetical plot of drawdown versus 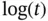for the Theis method.Figure 4.8 Schematic diagram of a vertical slice through an unconfined aquif...Figure 4.9 Weak solution to the porous medium equation showing a nondifferen...Figure 4.10 Location of the advancing front 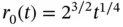as a function of time.

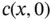4 Chapter 5Figure 5.1 Qualitative illustration of Taylor diffusion. (a) Parabolic veloc...Figure 5.2 Mechanical dispersion effects. (a) Solute spreading as a result o...Figure 5.3 Initial concentration profile for a sample initial‐value proble...Figure 5.4 Geometry of the method of characteristics, showing a hypothetical...Figure 5.5 (a) An admissible initial curve for a first‐order PDE. This curve...Figure 5.6 The solution 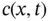to the moving plume problem at two different times...Figure 5.7 Graph of the fundamental solution to the heat equation showing th...Figure 5.8 Graph of moving front solutions 5.36 to the advection–diffusion e...Figure 5.9 Snapshot of a numerical solution to the moving‐front problem usin...Figure 5.10 Snapshot of a numerical solution to the moving‐front problem usi...Figure 5.11 (a) Linear isotherm. (b) Freundlich isotherms for different valu...Figure 5.12 Graph of the ramp‐like initial concentration profile for the ini...Figure 5.13 Characteristic curves associated with the initial‐value problem ...Figure 5.14 Resolution to the problem of intersecting characteristics in Fig...Figure 5.15 Chord on the isotherm defining the speed of the adsorbate concen...Figure 5.16 Graphs of the solution 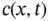at several time levels, showing the for...

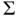5 Chapter 6Figure 6.1 A piece of smooth surface with boundary 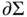, which is parametrize...Figure 6.2 A curved interface 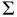with the pressure on the concave side being ...Figure 6.3 Wetting fluid 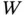and nonwetting fluid 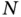in a tube with contact ang...Figure 6.4 Capillary rise of water in a tube open at the top to the air.Figure 6.5 Capillary rise of water in a bundle of tubes having different rad...Figure 6.6 Typical capillary pressure curves showing the effects of hysteres...Figure 6.7 Schematic profile of soil in the near‐surface region, showing the...Figure 6.8 Schematic diagram of a tensiometer showing the water‐saturated po...Figure 6.9 Graph of a typical pressure head 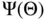for variably saturated flow in...Figure 6.10 Graph of a typical unsaturated hydraulic conductivity 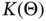for vari...Figure 6.11 An advancing moisture content front showing a wetting front, dow...Figure 6.12 Typical relative permeability curves.Figure 6.13 Typical fractional flow function associated with relative permea...Figure 6.14 One‐dimensional flow geometry used in the Buckley–Leverett probl...Figure 6.15 Ramp‐shaped initial condition used in the initial‐value problem ...Figure 6.16 Graphic solution to the Buckley–Leverett problem: Part (a) shows...Figure 6.17 Saturation shock in the solution to the Buckley–Leverett problem...Figure 6.18 Welge tangent construction to determine the saturation 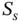at the ...Figure 6.19 Characteristic curves for the Buckley–Leverett problem showing t...Figure 6.20 Classical solution to the Buckley–Leverett problem with nonzero ...Figure 6.21 Characteristic curves for the Buckley–Leverett solution showing ...Figure 6.22 Oil production rate as a function of time predicted by the Buckl...Figure 6.23 Welge's graphic construction of the average oil saturation 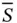at ...Figure 6.24 Schematic diagram of viscous fingering: A more mobile injected f...Figure 6.25 Geometry of the initially planar displacement front 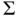separating...Figure 6.26 Perturbation 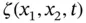to the initial displacement front 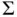.Figure 6.27 The perturbation as a level surface of the function 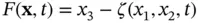, showing a...Figure 6.28 A ternary diagram for three‐phase saturations showing the geomet...Figure 6.29 Saturation profiles for gas, oil, and water used in Exercise 6.1...Figure 6.30 Hypothetical three‐phase relative permeability contour plots sho...Figure 6.31 Saturation ternary diagram showing the reduced ternary diagram a...Figure 6.32 Two families of integral curves in the reduced ternary diagram d...Figure 6.33 Two saturation routes connecting the constant states 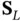and 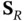via...Figure 6.34 Saturation profile for the three‐phase displacement modeled by t...