6 Chapter 7Figure 7.1 Flow chart for equation‐of‐state thermodynamic calculations in a ...
7 Appendix BFigure B.1 Cylindrical coordinates.Figure B.2 Spherical coordinates.
8 Appendix DFigure D.1 A parametrized surface 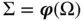 showing the unit normal vector
showing the unit normal vector 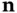 and the...
and the...
1 Cover Page
2 Table of Contents
3 Begin Reading
1 iii
2 iv
3 v
4 xi
5 xii
6 1
7 2
8 3
9 4
10 5
11 6
12 7
13 8
14 9
15 10
16 11
17 12
18 13
19 14
20 15
21 16
22 17
23 18
24 19
25 20
26 21
27 22
28 23
29 24
30 25
31 26
32 27
33 28
34 29
35 30
36 31
37 33
38 34
39 35
40 36
41 37
42 38
43 39
44 40
45 41
46 42
47 43
48 44
49 45
50 46
51 47
52 48
53 49
54 50
55 51
56 52
57 53
58 54
59 55
60 56
61 57
62 58
63 59
64 60
65 61
66 62
67 63
68 64
69 65
70 66
71 67
72 68
73 69
74 70
75 71
76 72
77 73
78 74
79 75
80 76
81 77
82 78
83 79
84 80
85 81
86 82
87 83
88 84
89 85
90 86
91 87
92 88
93 89
94 90
95 91
96 92
97 93
98 95
99 96
100 97
101 98
102 99
103 100
104 101
105 102
106 103
107 104
108 105
109 106
110 107
111 108
112 109
113 110
114 111
115 112
116 113
117 114
118 115
119 116
120 117
121 118
122 119
123 121
124 122
125 123
126 124
127 125
128 126
129 127
130 128
131 129
132 130
133 131
134 132
135 133
136 134
137 135
138 136
139 137
140 138
141 139
142 140
143 141
144 142
145 143
146 144
147 145
148 146
149 147
150 148
151 149
152 150
153 151
154 152
155 153
156 154
157 155
158 156
159 157
160 158
161 159
162 160
163 161
164 162
165 163
166 164
167 165
168 166
169 167
170 168
171 169
172 170
173 171
174 172
175 173
176 174
177 175
178 176
179 177
180 178
181 179
182 180
183 181
184 182
185 183
186 184
187 185
188 186
189 187
190 189
191 190
192 191
193 193
194 194
195 195
196 196
197 197
198 198
199 199
200 200
201 201
202 202
203 203
204 204
205 205
206 206
207 207
208 208
209 209
210 210
211 211
212 212
213 213
Seldom turns out the way it does in the song.
Robert Hunter
This book provides a semester‐length course in the mathematics of fluid flows in porous media. Over a 20‐year span, I taught such a course every few years to doctoral students in engineering, mathematics, and geophysics. Most of these students' research involved flow and transport in groundwater aquifers, soils, and petroleum reservoirs. The students' mathematical backgrounds ranged from standard undergraduate engineering requirements to more advanced, graduate‐level training.
The book emphasizes analytic aspects of flows in porous media. This focus may seem odd: Most mathematically oriented scholarship in the area is computational in nature, owing both to the heterogeneity of natural porous media and to the inherent nonlinearity of many underground flow models. Nevertheless, while many superb books cover computational methods for flows in porous media, intelligent design of numerical approximations also requires a grasp of certain analytic questions:
Where do the governing equations come from?
What physics do they model, and what physics do they neglect?
What qualitative properties do their solutions exhibit?
Where appropriate, the book discusses numerical implications of these questions.
The exposition should be accessible to anyone who has completed a baccalaureate program in engineering, mathematics, or physics at a US university. The book makes extensive use of multivariable calculus, including the integral theorems of vector field theory, and ordinary differential equations. Several sections exploit concepts from first‐semester linear algebra. No prior study of partial differential equations is necessary, but some exposure to them is helpful.
After a brief introduction in Chapter 1, Chapter 2introduces the mass and momentum balance laws from which the governing partial differential equations arise. This chapter sets the stage for a pattern that appears throughout the book: We derive governing equations, then analyze representative or generic solutions to infer important attributes of the flows.
Chapters 3through 5examine models of single‐fluid flows, followed by models of the transport of chemical species in the subsurface. After a discussion in Chapter 6of multiphase flows, traditionally the province of oil reservoir engineers but now also important in groundwater contaminant hydrology and carbon dioxide sequestration, Chapter 7provides an overview multifluid, multispecies flows, also called compositional flows. This level of complexity admits few analytic solutions. Therefore, Chapter 7focuses on model formulation.
Two features of the book deserve comment.
Over 100 exercises, most of them straightforward, appear throughout the text. Their main purpose is to engage the reader in some of the steps required to develop the theory.
There are four appendices. The first simply lists symbols that have dedicated physical meanings. The remaining appendices cover three common curvilinear coordinate systems, the Buckingham Pi theorem of dimensional analysis, and some aspects of surface integrals. While needed at certain junctures in the text, these topics seem ancillary to the book's main focus.
I owe thanks to dozens of students at the University of Wyoming who endured early versions of the notes for this book. These men and women convinced me of its utility and offered many corrections and suggestions for improvement. Professor Frederico Furtado kindly offered additional corrections, generous encouragement, and insights deeper than he will admit. I also owe sincerest thanks to my colleagues in the University of Wyoming's Department of Mathematics and Statistics, from whom I have learned a lot. I cannot have asked for a better academic home. Finally, my wife, Adele Aldrich, deserves more gratitude than I know how to express, for her support through the entire process.
Myron B. Allen
Laramie, Wyoming
December, 2020
1 Introduction
1.1 Historical Setting
The mathematical theory of fluid flows in porous media has a distinguished history. Most of this theory ultimately rests on Henry Darcy's 1856 engineering study [43], summarized in Section 3.1, of the water supplies in Dijon, France. A year after the publication of this meticulous and seminal work, Jules Dupuit [49], a giant among early groundwater scientists, recognized that Darcy's findings implied a differential equation. This observation proved to be crucial. For the next 75 years or so, the subject grew to encompass problems in multiple space dimensions—hence partial differential equation s( PDE s)—with major contributions emerging mainly from the groundwater hydrology community. Pioneers included Joseph Boussinesq [25, 26], Philipp Forchheimer [53, 54], Charles S. Slichter [136], Edgar Buckingham [30], and Lorenzo A. Richards [129].
Читать дальше

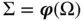 showing the unit normal vector
showing the unit normal vector 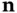 and the...
and the...










