The Mathematics of Fluid Flow Through Porous Media
Myron B. Allen
University of Wyoming
This edition first published 2021
© 2021 John Wiley & Sons, Inc.
All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording or otherwise, except as permitted by law. Advice on how to obtain permission to reuse material from this title is available at http://www.wiley.com/go/permissions.
The right of Myron B. Allen to be identified as the author of this work has been asserted in accordance with law.
Registered Office
John Wiley & Sons, Inc., 111 River Street, Hoboken, NJ 07030, USA
Editorial Office
111 River Street, Hoboken, NJ 07030, USA
For details of our global editorial offices, customer services, and more information about Wiley products visit us at www.wiley.com.
Wiley also publishes its books in a variety of electronic formats and by print‐on‐demand. Some content that appears in standard print versions of this book may not be available in other formats.
Limit of Liability/Disclaimer of Warranty
The contents of this work are intended to further general scientific research, understanding, and discussion only and are not intended and should not be relied upon as recommending or promoting scientific method, diagnosis, or treatment by physicians for any particular patient. In view of ongoing research, equipment modifications, changes in governmental regulations, and the constant flow of information relating to the use of medicines, equipment, and devices, the reader is urged to review and evaluate the information provided in the package insert or instructions for each medicine, equipment, or device for, among other things, any changes in the instructions or indication of usage and for added warnings and precautions. While the publisher and authors have used their best efforts in preparing this work, they make no representations or warranties with respect to the accuracy or completeness of the contents of this work and specifically disclaim all warranties, including without limitation any implied warranties of merchantability or fitness for a particular purpose. No warranty may be created or extended by sales representatives, written sales materials or promotional statements for this work. The fact that an organization, website, or product is referred to in this work as a citation and/or potential source of further information does not mean that the publisher and authors endorse the information or services the organization, website, or product may provide or recommendations it may make. This work is sold with the understanding that the publisher is not engaged in rendering professional services. The advice and strategies contained herein may not be suitable for your situation. You should consult with a specialist where appropriate. Further, readers should be aware that websites listed in this work may have changed or disappeared between when this work was written and when it is read. Neither the publisher nor authors shall be liable for any loss of profit or any other commercial damages, including but not limited to special, incidental, consequential, or other damages.
Library of Congress Cataloging‐in‐Publication Data Applied for:
ISBN: 9781119663843
Cover Design: Wiley
Cover Image: © Myron B. Allen
To Professor George F. Pinder, who has lit the path for so many.
1 Cover
2 Title page The Mathematics of Fluid Flow Through Porous Media Myron B. Allen University of Wyoming
3 Copyright
4 Preface
5 1: Introduction1.1 Historical Setting 1.2 Partial Differential Equations (PDEs) 1.3 Dimensions and Units 1.4 Limitations in Scope
6 2: Mechanics 2.1 Kinematics of Simple Continua 2.2 Balance Laws for Simple Continua 2.3 Constitutive Relationships 2.4 Two Classic Problems in Fluid Mechanics 2.5 Multiconstituent Continua
7 3: Single‐fluid Flow Equations 3.1 Darcy's Law 3.2 Non‐Darcy Flows 3.3 The Single‐fluid Flow Equation 3.4 Potential Form of the Flow Equation 3.5 Areal Flow Equation 3.6 Variational Forms for Steady Flow 3.7 Flow in Anisotropic Porous Media
8 4: Single‐fluid Flow Problems 4.1 Steady Areal Flows with Wells 4.2 The Theis Model for Transient Flows 4.3 Boussinesq and Porous Medium Equations
9 5: Solute Transport 5.1 The Transport Equation 5.2 One‐Dimensional Advection 5.3 The Advection–Diffusion Equation 5.4 Transport with Adsorption
10 6: Multifluid Flows 6.1 Capillarity 6.2 Variably Saturated Flow 6.3 Two‐fluid Flows 6.4 The Buckley–Leverett Problem 6.5 Viscous Fingering 6.6 Three‐fluid Flows 6.7 Three‐fluid Fractional Flow Analysis
11 7: Flows With Mass Exchange 7.1 General Compositional Equations 7.2 Black‐oil Models 7.3 Compositional Flows in Porous Media 7.4 Fluid‐phase Thermodynamics
12 Appendix A: Dedicated Symbols
13 Appendix B: Useful Curvilinear Coordinates B.1 Polar Coordinates B.2 Cylindrical Coordinates B.3 Spherical Coordinates
14 Appendix C: The Buckingham Pi Theorem C.1 Physical Dimensions and Units C.2 The Buckingham Theorem
15 Appendix D: Surface Integrals D.1 Definition of a Surface Integral D.2 The Stokes Theorem D.3 A Corollary to the Stokes Theorem
16 Bibliography
17 Index
18 End User License Agreement
1 Chapter 3Table 3.1 Isotropic, anisotropic, homogeneous, and inhomogeneous permeability...
2 Chapter 7Table 7.1 Phases in a compositional model.Table 7.2 Derived quantities used in compositional modeling.Table 7.3 Partitioning of pseudospecies in a black‐oil model.Table 7.4 Molar quantities used in compositional reservoir modeling.
3 Appendix ATable A.1 Dedicated symbols for physical quantities.
1 Chapter 2 Figure 2.1 A reference configuration of a body, showing the referential coor... Figure 2.2 The deformation mapping the reference configuration  onto the bo... Figure 2.3 Regions
onto the bo... Figure 2.3 Regions  and
and  occupied by a body in two reference configuration... Figure 2.4 Orthonormal basis vectors defining a Cartesian coordinate system.... Figure 2.5 A time‐independent region
occupied by a body in two reference configuration... Figure 2.4 Orthonormal basis vectors defining a Cartesian coordinate system.... Figure 2.5 A time‐independent region 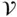 having oriented boundary
having oriented boundary 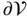 and unit o... Figure 2.6 A region
and unit o... Figure 2.6 A region 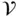 in three‐dimensional space with unit outward normal ve... Figure 2.7 A cube of material illustrating the interpretations of entries of... Figure 2.8 Coordinate system used to define the depth function
in three‐dimensional space with unit outward normal ve... Figure 2.7 A cube of material illustrating the interpretations of entries of... Figure 2.8 Coordinate system used to define the depth function 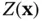 . Figure 2.9 Geometry of the Stokes problem for slow fluid flow around a solid... Figure 2.10 Profile of flow through a thin circular cylinder having radius
. Figure 2.9 Geometry of the Stokes problem for slow fluid flow around a solid... Figure 2.10 Profile of flow through a thin circular cylinder having radius 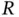 Figure 2.11 A reference configuration and the deformation at times
Figure 2.11 A reference configuration and the deformation at times 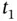 and
and 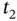 f... Figure 2.12 Sketch of a fluid‐saturated porous medium showing three possible... Figure 2.13 Conceptual plot of REV‐averaged volume fraction versus radius of...
f... Figure 2.12 Sketch of a fluid‐saturated porous medium showing three possible... Figure 2.13 Conceptual plot of REV‐averaged volume fraction versus radius of...
Читать дальше

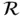 onto the bo... Figure 2.3 Regions
onto the bo... Figure 2.3 Regions 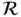 and
and 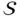 occupied by a body in two reference configuration... Figure 2.4 Orthonormal basis vectors defining a Cartesian coordinate system.... Figure 2.5 A time‐independent region
occupied by a body in two reference configuration... Figure 2.4 Orthonormal basis vectors defining a Cartesian coordinate system.... Figure 2.5 A time‐independent region 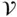 having oriented boundary
having oriented boundary 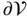 and unit o... Figure 2.6 A region
and unit o... Figure 2.6 A region 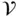 in three‐dimensional space with unit outward normal ve... Figure 2.7 A cube of material illustrating the interpretations of entries of... Figure 2.8 Coordinate system used to define the depth function
in three‐dimensional space with unit outward normal ve... Figure 2.7 A cube of material illustrating the interpretations of entries of... Figure 2.8 Coordinate system used to define the depth function 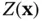 . Figure 2.9 Geometry of the Stokes problem for slow fluid flow around a solid... Figure 2.10 Profile of flow through a thin circular cylinder having radius
. Figure 2.9 Geometry of the Stokes problem for slow fluid flow around a solid... Figure 2.10 Profile of flow through a thin circular cylinder having radius 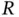 Figure 2.11 A reference configuration and the deformation at times
Figure 2.11 A reference configuration and the deformation at times 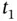 and
and 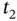 f... Figure 2.12 Sketch of a fluid‐saturated porous medium showing three possible... Figure 2.13 Conceptual plot of REV‐averaged volume fraction versus radius of...
f... Figure 2.12 Sketch of a fluid‐saturated porous medium showing three possible... Figure 2.13 Conceptual plot of REV‐averaged volume fraction versus radius of...










