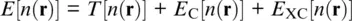As mentioned at the beginning of this section, experimentally determined sound wave velocities are ideally combined with measurements of density or volume strain at the same pressure and temperature. Densities are routinely determined by X‐ray diffraction, and all methods outlined above can in principle be combined with X‐ray diffraction experiments. X‐ray diffraction at high pressures has been treated in numerous review articles (Angel et al., 2000; Boffa Ballaran et al., 2013; Miletich et al., 2005; Norby and Schwarz, 2008) and is used to determine the volume of the crystallographic unit cell of a crystalline material. Particularly instructive examples of combining measurements of elastic properties with measurements of unit cell volumes were given by Zha et al. (1998, 2000), who determined bulk moduli as a function of volume by combining single‐crystal Brillouin spectroscopy and X‐ray diffraction. Combinations of bulk moduli K and unit cell volumes V at different compression states define the function K ( V ) that, upon integration, gives a direct measure for pressure:
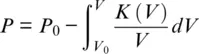
Sample sizes in diamond anvil cells are very small, and samples are surrounded by heater and thermal insulation materials in multi‐anvil presses so that, in most cases, intense and focused X‐rays from synchrotron sources are required to generate diffraction patterns of suitable quality. Converting the unit cell volume to density requires information on the atomic content of the unit cell and hence on the chemical composition of the material. Uncertainties on molar masses of chemically complex materials typically subvert the high precision on unit cell volumes achievable with modern X‐ray diffraction techniques. Note also that densities based on X‐ray diffraction do not capture amorphous materials or porosity that might be present along grain boundaries or cracks in polycrystalline materials. A rather new technique to determine the bulk modulus uses synchrotron X‐ray diffraction to capture the elastic response of a polycrystalline sample that is subjected to cyclic loading at seismic frequencies. For this type of experiment, a DAC is attached to a piezoelectric actuator that generates small pressure oscillations. The resulting oscillations in unit cell volume can be measured by recording the time-resolved diffraction of intense X-rays with sufficiently fast and sensitive detectors and be analyzed to constrain the bulk modulus. Marquardt et al. (2018) successfully used this technique to probe the softening of the bulk modulus across the spin transition in ferropericlase at seismic frequencies. When combined with resistive heating, piezo‐driven DACs may facilitate cyclic loading experiments at combined high pressures and high temperatures (Méndez et al., 2020).
Quantum‐mechanical computations and molecular dynamic simulations have evolved to powerful tools in predicting the elastic properties of minerals at high pressures and high temperatures and complement experiments for conditions that are not readily accessible with current experimental methods (Karki et al., 2001a; Stixrude et al., 1998). First‐principle calculations are based on the Schrödinger equation:
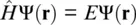
that yields the total energy E of a system of electrons and atomic nuclei as the eigenvalue of the Hamiltonian operator 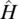 that is applied to the multi‐particle wave function Ψ( r). In density functional theory (DFT), the Hamiltonian operator is broken down into contributions of the kinetic energy T of non‐interacting electrons, the electrostatic potential energy E C, and the exchange‐correlation energy E XCthat describes the electron‐electron interaction, all of which are functionals of the electron density n ( r) that changes with the location r(Hohenberg and Kohn, 1964; Kohn and Sham, 1965). The total energy can then be expressed in terms of the electron density:
that is applied to the multi‐particle wave function Ψ( r). In density functional theory (DFT), the Hamiltonian operator is broken down into contributions of the kinetic energy T of non‐interacting electrons, the electrostatic potential energy E C, and the exchange‐correlation energy E XCthat describes the electron‐electron interaction, all of which are functionals of the electron density n ( r) that changes with the location r(Hohenberg and Kohn, 1964; Kohn and Sham, 1965). The total energy can then be expressed in terms of the electron density:
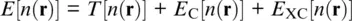
While the functionals of kinetic and potential energies can be evaluated exactly, formulations for the exchange‐correlation energy rely on approximations (Karki et al., 2001a; Perdew & Ruzsinszky, 2010; Stixrude et al., 1998). These approximations allow computing the total energy E for a given arrangement of atoms, i.e., for a crystal structure. The forces acting between atoms, also called Hellmann‐Feynman forces, can be found by evaluating the changes in energy that result from small perturbations of the atomic arrangement (Baroni et al., 2001). When the perturbation of the atomic arrangement is chosen to correspond to a homogeneous strain, the resulting stresses (Nielsen and Martin, 1985) and hence elastic properties can be derived (Baroni et al., 1987a, 2001; Wentzcovitch et al., 1995). Alternatively, an external pressure can be applied to the simulation cell, and the resulting forces and stresses be minimized by relaxing the atomic positions and the shape of the simulation cell (Wentzcovitch et al., 1995, 1993). Note that, apart from being intentionally displaced or being relaxed to their equilibrium configuration, atomic nuclei remain static in these calculations. The results of such static DFT calculations can in principle be compared with those of experiments at ambient temperature as thermal contributions at 298 K are expected to be fairly small for most materials.
In most cases, the exchange‐correlation contribution is evaluated based on either the local density approximation (LDA) or on generalized gradient approximations (GGA). The LDA approximates the exchange‐correlation potential at each point rby the exchange‐correlation potential of a uniform electron gas with the density n ( r) at this point. GGA also take into account gradients in electron density when evaluating the exchange‐correlation potential. Both LDA and GGA have proven successful in reproducing the elastic properties of many mantle minerals where experimental results are available for comparison. However, LDA appears to systematically overestimate bonding forces, i.e., leading to slightly higher elastic moduli and smaller volumes, while GGA tends to underestimate bonding forces with opposite effects on elastic properties and volumes (Karki et al., 2001a). Another aspect becomes important when computing properties of compounds containing transition metal or lanthanide atoms such as iron and its cations that are present in many mantle minerals. Both LDA and GGA take into account mutual repulsion between electrons in an inhomogeneous but diffuse gas of electrons. This approximation breaks down for electrons in the less diffuse d and f orbitals of transition metal and lanthanide atoms as these electrons become effectively localized by the additional repulsion they experience from electrons in similar orbitals on the same and neighboring atoms (e.g., Cox, 1987; Hubbard, 1963). This localization is the reason for the insulating or semi‐conducting behavior of some transition metal oxides, such as FeO, despite of their partially filled d orbitals.
By far the most common strategy to account for the repulsion between localized d electrons is to add an energy term E Uthat depends on the Hubbard parameter U and on the occupation numbers of d orbitals (Anisimov et al., 1997, 1991; Cococcioni, 2010; Cococcioni and de Gironcoli, 2005). This approach, referred to as LDA+U or GGA+U, can reduce discrepancies between predicted and experimentally observed elastic properties (Stackhouse et al., 2010) and led to substantial improvements in treating spin transitions of ferrous and ferric iron with DFT calculations (Hsu et al., 2011, 2010a, 2010b; Persson et al., 2006; Tsuchiya et al., 2006). Despite important progress in modeling the electronic properties of iron cations in oxides and silicates, elastic properties extracted from DFT computations still seem to deviate significantly from experimental observations in particular across spin transitions in major mantle minerals (Fu et al., 2018; Shukla et al., 2016; Wu et al., 2013), highlighting persistent challenges in the treatment of localized d electrons.
Читать дальше

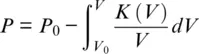
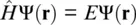
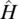 that is applied to the multi‐particle wave function Ψ( r). In density functional theory (DFT), the Hamiltonian operator is broken down into contributions of the kinetic energy T of non‐interacting electrons, the electrostatic potential energy E C, and the exchange‐correlation energy E XCthat describes the electron‐electron interaction, all of which are functionals of the electron density n ( r) that changes with the location r(Hohenberg and Kohn, 1964; Kohn and Sham, 1965). The total energy can then be expressed in terms of the electron density:
that is applied to the multi‐particle wave function Ψ( r). In density functional theory (DFT), the Hamiltonian operator is broken down into contributions of the kinetic energy T of non‐interacting electrons, the electrostatic potential energy E C, and the exchange‐correlation energy E XCthat describes the electron‐electron interaction, all of which are functionals of the electron density n ( r) that changes with the location r(Hohenberg and Kohn, 1964; Kohn and Sham, 1965). The total energy can then be expressed in terms of the electron density: