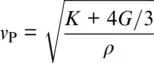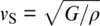Mantle Convection and Surface Expressions

Once the elastic properties of individual minerals have been combined to bulk and shear moduli of an isotropic polymineralic rock, the propagation velocities v of longitudinal waves (P) and transverse or shear waves (S) can be calculated by:

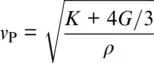
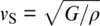
The density ρ of the rock is computed by combining the molar masses and volumes of all minerals according to their abundances. Note that wave velocities discussed throughout this chapter are based on the elastic response of minerals and rocks only and do not include corrections for anelastic behavior that might affect wave velocities at seismic frequencies and at high temperatures (Jackson, 2015; Karato, 1993).

Finite‐strain theory describes the elastic stiffnesses or moduli as functions of volume and temperature. The parameters needed for this description are therefore best determined from data sets that relate elastic stiffnesses or moduli with the corresponding volume (or density) and temperature. Since sound wave velocities are combinations of elastic moduli and density, they contain information on the elastic properties that is best retrieved when volume and temperature are determined along with sound wave velocities. Alternatively, volume can be inferred from pressure measurements via an equation of state (EOS) that relates pressure to volume and temperature. More information on theoretical and experimental aspects of high‐pressure equations of state for solids has been summarized in recent review articles (Angel, 2000; Angel et al., 2014; Holzapfel, 2009; Stacey & Davis, 2004). Here, I give a brief overview of methods that constrain elastic properties other than the EOS. More detailed introductions into these and other methods to characterize the elastic properties of minerals can be found in Schreuer and Haussühl (2005) and in Angel et al. (2009).

The elastic stiffness tensor completely describes the elastic anisotropy of a crystal and hence also determines the velocities of sound waves travelling in different crystallographic directions. The components of the elastic stiffness tensor can therefore be derived by measuring the velocities of sound waves that propagate through a single crystal along a set of different directions selected so as to adequately sample the elastic anisotropy of the crystal. The minimum number of individual measurements depends on the number of independent components c ijkland hence on the crystal symmetry. At high pressures, sound wave velocities can be determined using light scattering techniques on single crystals contained in diamond anvil cells (DAC). Both Brillouin spectroscopy and impulsive stimulated scattering (ISS) are based on inelastic scattering of light by sound waves (Cummins & Schoen, 1972; Dil, 1982; Fayer, 1982). The applications of Brillouin spectroscopy and ISS to determine elastic properties at high pressures have been reviewed by Speziale et al. (2014) and by Abramson et al. (1999), respectively. Light scattering experiments on single crystals compressed in DACs have proven successful in deriving full elastic stiffness tensors of mantle minerals up to pressures of the lower mantle (Crowhurst et al., 2008; Kurnosov et al., 2017; Marquardt et al., 2009c; Yang et al., 2015; Zhang et al., 2021). At combined high pressures and high temperatures, elastic stiffness tensors have been determined using Brillouin spectroscopy by heating single crystals inside DACs using resistive heaters or infrared lasers (Li et al., 2016; Mao et al., 2015; Yang et al., 2016; Zhang & Bass, 2016).

Resistive heaters for DACs commonly consist of platinum wires coiled on a ceramic ring that is placed around the opposing diamond anvils with the pressure chamber between their tips (Kantor et al., 2012; Sinogeikin et al., 2006). With this configuration, the pressure chamber containing the sample is heated from the outside together with the diamond anvils and the gasket. Heating and oxidation of diamond anvils and metallic gaskets can destabilize the pressure chamber and even cause it to collapse. Therefore, measurements of elastic properties using resistive heating of samples contained in DACs have so far been limited to temperatures of about 900 K. Such experiments require purging of DAC environments with inert or reducing gases, typically mixtures of argon and hydrogen, to prevent oxidation of diamonds and gaskets. Higher temperatures can be achieved with graphite heaters and by surrounding the DAC with a vacuum chamber (Immoor et al., 2020; Liermann et al., 2009). Setups with graphite heaters have been developed for X‐ray diffraction experiments and could potentially be combined with measurements of elastic properties. When heating DACs with external heaters, temperatures are typically measured with thermocouples that are placed close to but outside of the pressure chamber. Besides those limitations, resistive heaters create a temperature field that can be assumed to be nearly homogeneous across the pressure chamber and can be held stable for long enough periods of time to perform light scattering and X‐ray diffraction experiments on samples inside DACs.

Substantially higher temperatures can be achieved by using infrared (IR) lasers to directly heat a sample inside the pressure chamber of a DAC through the absorption of IR radiation. For a given material, the strength of absorption and hence the heating efficiency depend on the wavelength of the IR laser radiation. The IR radiation emitted by common rare‐earth‐element (REE) lasers, e.g., lasers based on REE‐doped host crystals or optical fibers, is centered at wavelengths between 1 μm and 3 μm and efficiently absorbed by metals and by most opaque or iron‐rich minerals. Light scattering experiments, however, are commonly performed on optically transparent materials, such as oxides and silicates with lower iron contents, that may not absorb IR radiation at wavelengths around 1–3 μm efficiently enough for uniform and steady heating. CO 2gas lasers emit IR radiation with wavelengths of about 10 μm that is absorbed even by many optically transparent materials. As a consequence, CO 2lasers have been used to heat transparent mineral samples while probing their elastic properties with light scattering (Kurnosov et al., 2019; Murakami et al., 2009a; Sinogeikin et al., 2004; Zhang et al., 2015).

Requirements of uniform heating as well as stabilization and accurate assessment of temperatures impose particular challenges on laser‐heating experiments. Typical sample sizes for light scattering experiments on the order of several tens to hundred micrometers may exceed the sizes of hot spots generated by IR lasers. As a result, samples may not be heated uniformly, and the resulting thermal gradients can bias the measurements of both temperature and elastic properties. During laser‐heating experiments, temperatures are determined by analyzing the thermal emission spectrum of the hot sample. Modern optical instrumentation allows combining spectral with spatial information of the hot spot to generate temperature maps that reveal thermal gradients and facilitate more accurate temperature measurements (Campbell, 2008; Kavner & Nugent, 2008; Rainey and Kavner, 2014). Analyses of laser‐heated hot spots indicate that temperatures may vary by several hundreds of kelvins over a few tens of micrometers across the hot spot. The interaction of the sample with the IR laser often changes in the course of a laser‐heating experiment and may lead to temporal temperature fluctuations in addition to thermal gradients. As a consequence, uncertainties of temperature measurements on laser‐heated samples tend to be on the order of several hundred kelvins. The combination of sound wave velocity measurements on samples held at high pressures inside DACs with laser heating remains one of the major experimental challenges in mineral physics. The potential to determine elastic properties at pressures and temperatures that resemble those predicted to prevail throughout Earth’s mantle has motivated first efforts to combine Brillouin spectroscopy with laser heating (Kurnosov et al., 2019; Murakami et al., 2009a; Sinogeikin et al., 2004; Zhang et al., 2015) and led to successful measurements of sound wave velocities at combined high pressures and high temperatures (Murakami et al., 2012; Zhang & Bass, 2016).